48. 旋转图像：

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

样例 1：

输入：
	matrix = [[1,2,3],[4,5,6],[7,8,9]]
	
输出：
	[[7,4,1],[8,5,2],[9,6,3]]

样例 2：

输入：
	matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
	
输出：
	[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

分析：

• 面对这道算法题目，二当家的陷入了沉思。
• 一般最容易想到的就是遍历矩阵的每个值，放到一个新矩阵里面。
• 使用原矩阵最大的问题就是，我们知道一个位置的值旋转后应该放到哪里去，但是新的位置上同样有值，不能直接覆盖掉。
• 有经验的大佬们可以想到用翻转代替旋转，把旋转分解为2步，翻转的特点是两两交换，不会覆盖丢失原值。
• 事实上还有一个很好的办法，矩阵，一个正方形，中心对称，可以均分为4份（边长为奇数时，中心点不需要移动，可以排除，其他点仍然可以4等分），然后遍历其中一份，将4份中对应位置的值做顺序交换。
  

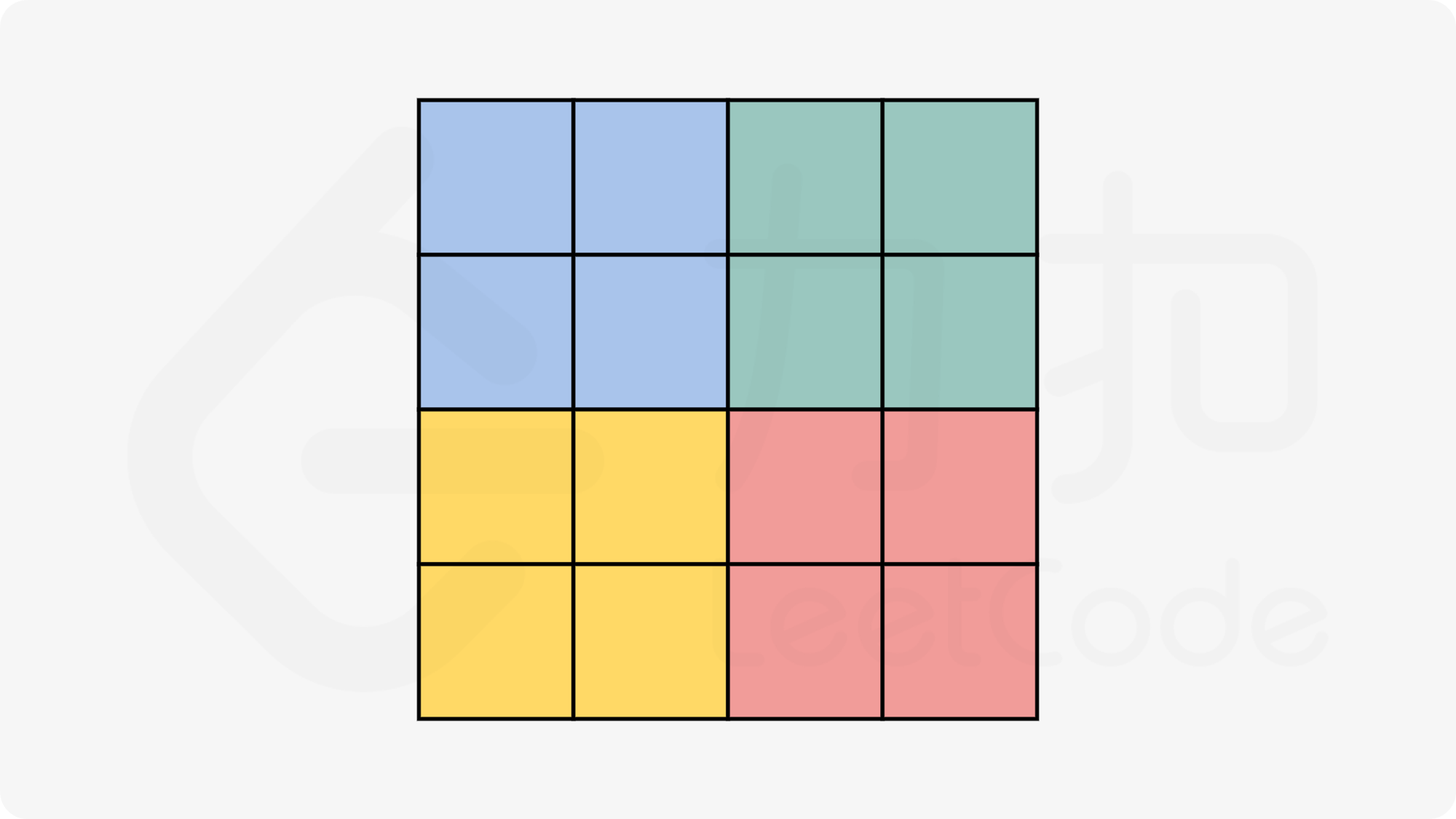
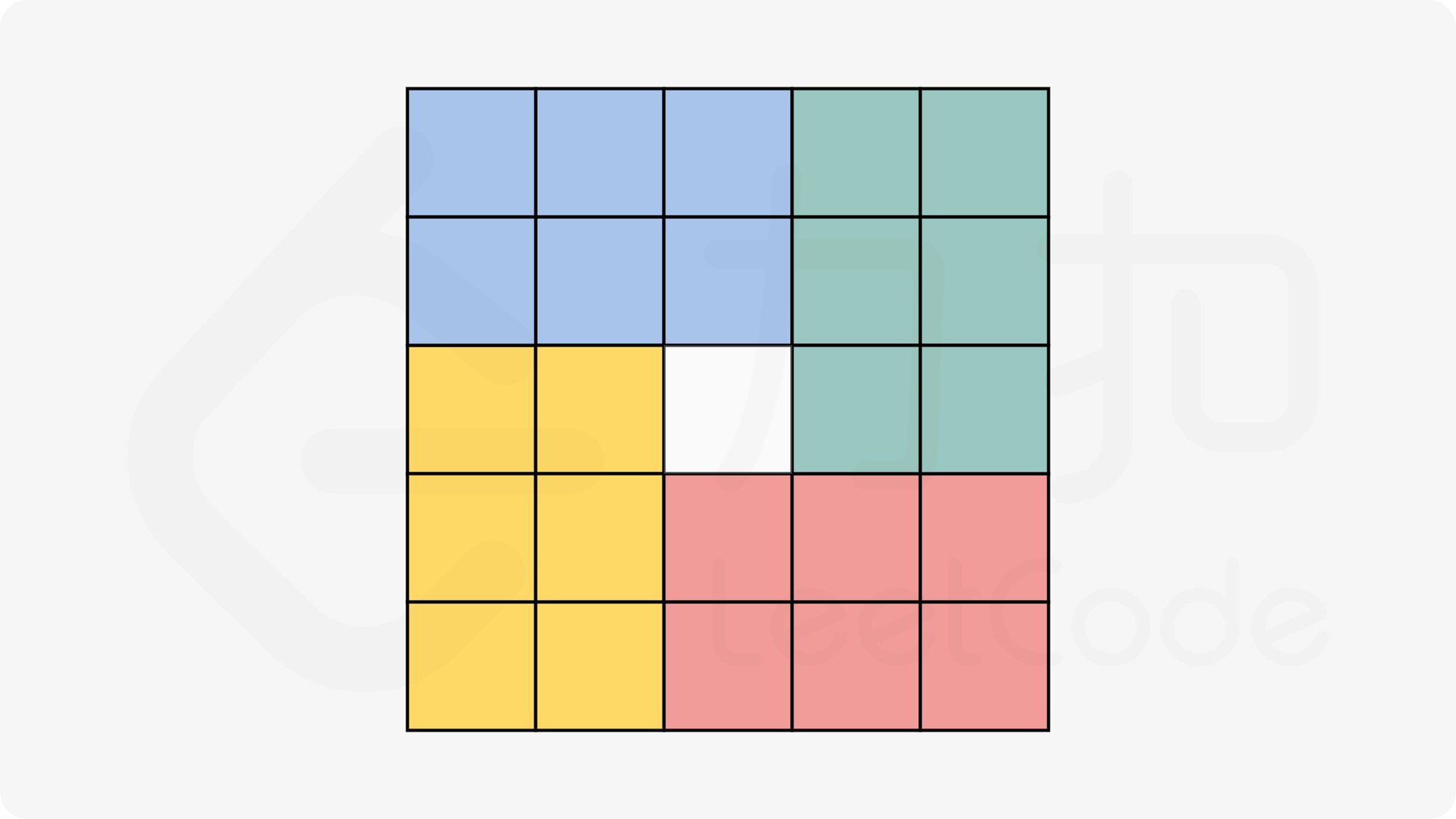
题解：

rust：

• 两次翻转：

impl Solution {
    pub fn rotate(matrix: &mut Vec<Vec<i32>>) {
        let n = matrix.len();

        // 水平翻转
        (0..n / 2).for_each(|i| {
            (0..n).for_each(|j| {
                let temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            });
        });

        // 主对角线翻转
        (0..n).for_each(|i| {
            (0..i).for_each(|j| {
                let temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            });
        });
    }
}

• 原地旋转：

impl Solution {
    pub fn rotate(matrix: &mut Vec<Vec<i32>>) {
        let n = matrix.len();

        (0..n / 2).for_each(|i| {
            (0..(n + 1) / 2).for_each(|j| {
                let temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            });
        });
    }
}

go：

func rotate(matrix [][]int)  {
    n := len(matrix)

	// 水平翻转
	for i := 0; i < n/2; i++ {
		matrix[i], matrix[n-1-i] = matrix[n-1-i], matrix[i]
	}

	// 主对角线翻转
	for i := 0; i < n; i++ {
		for j := 0; j < i; j++ {
			matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
		}
	}
}

c++：

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();

        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                swap(matrix[i][j], matrix[n - i - 1][j]);
            }
        }

        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};

c：

void rotate(int** matrix, int matrixSize, int* matrixColSize){
    // 水平翻转
    for (int i = 0; i < matrixSize / 2; ++i) {
        for (int j = 0; j < matrixSize; ++j) {
            int temp = matrix[i][j];
            matrix[i][j] = matrix[matrixSize - i - 1][j];
            matrix[matrixSize - i - 1][j] = temp;
        }
    }

    // 主对角线翻转
    for (int i = 0; i < matrixSize; ++i) {
        for (int j = 0; j < i; ++j) {
            int temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }
}

python：

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """

        n = len(matrix)

        # 水平翻转
        for i in range(n // 2):
            for j in range(n):
                matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]

        # 主对角线翻转
        for i in range(n):
            for j in range(i):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

java：

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;

        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }
        
        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】~
放弃不难，但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子：https://le-yi.blog.csdn.net/ 博客原创~