• 博主简介：努力学习的22级计科生
• 博主主页： @是瑶瑶子啦
• 所属专栏: LeetCode每日一题–进击大厂

前言：动规五部曲

以下是《代码随想录》作者总结的动规五部曲

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式（状态转移方程）
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

1、509. 斐波那契数

509. 斐波那契数

class Solution {
public:
    int fib(int n) {
        if(n==0||n==1) return n;
        //basic case
        int a0 = 0;
        int a1 = 1;

        int ai = 0;

        for(int i = 2; i <= n; i++){
            ai = a0+a1;//a[i] = a[i-2]+a[i-1]

            //滚动更新
            a0 = a1;
            a1 = ai;
        }
        return ai;
    }
};

• 使用动态规划，转移方程为：a[i] = a[i-2]+a[i-1]
• 由于斐波那契数列当前状态n只与n-2和n-1有关，所以只需要开两个变量，存储两个状态即可，直接把空间复杂度从O(n)将为O(1)

2、322. 零钱兑换

322. 零钱兑换

🌻步骤

1. dp数组以及下标含义：dp[i]表示目标金额为i时的,至少选择dp[i]枚硬币
2. 状态转移方程
   
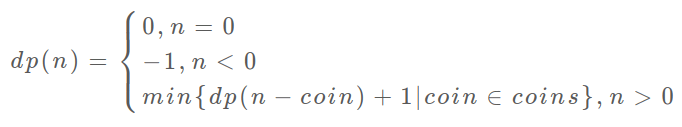
3. dp数组初识别

	//数组大小为amount+1,dp[i]初始化为amount+1(达不到的，初始化一个大的值）
	vector<int> dp(amount + 1, amount + 1)
	//base case
	dp[0] = 0;//目标金额为0，不用选择

为啥不直接初始化为 int 型的最大值 Integer.MAX_VALUE 呢？因为后面有 dp[i - coin] + 1，这就会导致整型溢出。

4. 确定遍历顺序:自底向上

🏄🏻‍♀️完整代码

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {

        //1)dp数组初始化
        vector<int> dp(amount+1,amount+1);
        dp[0] = 0;

        //2)自底向上遍历(遍历子问题，求解子问题最优解)
        for(int i = 0; i <dp.size(); i++){

            //下面的for求出dp[i],外层循环结束，dp[amount]得解
            for(int coin : coins){
                if(i - coin < 0){//选择了面值为coin的硬币，子问题无解
                    continue;
                }
                dp[i] = min(dp[i],1 + dp[i-coin]);//状态转移方程
            }
        }

        return (dp[amount] == amount + 1 ? -1 : dp[amount]);

    }
};

3、300. 最长递增子序列

300. 最长递增子序列

🌷数学归纳法求解状态转移方程

• 数学归纳法：假设在k<n时，结论成立，根据前面的假设，推出k = n时的结论。若能推出，则证明在k 为任何数时成立
• 对应到动态规划：假设d[0] … d[i-1]已经全部推出，然后反问自己：能否根据已经推出来的d[i-1]等，计算d[i]🌟
• ⭐前提：搞懂d[i]以及下标i的含义！

🌻步骤

1. 确定dp[i]以及下标i的含义：
   我觉得这步是蛮难的其实。看了题解才知道，dp[i]代表以nums[i]结尾的最长递增子序列。（dp数组的最大值就是答案）
2. 递推公式：
   求解dp[i]，可以先找到序列尾元素小于nums[i]的dp[x](遍历即可），然后+1,再取最大值即可求得dp[i]。（递推过程）
3. dp[i]数组初始化：dp[1~i] = 1(最不行也包括了自身！）
4. 遍历顺序：自底向上（因为dp[i]需要前面确定了，才能确定！）

🏄🏻‍♀️完整代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        //dp数组的定义和初始化：dp[i]表示以num[i]结尾的最长递增子序列
        vector<int> dp(nums.size(),1);

        //遍历，自底向上，确定dp[i]的值
        for (int i = 0; i < nums.size(); i++){
            //假设以知1~i-1的dp值，通过递推求dp[i]
            for(int j = 0; j < i; j++){
                if(nums[j]<nums[i]){
                    dp[i] = max(dp[i],1+dp[j]);
                }
            }
        }

        //最终结果是dp数组中的最大值
        int ans = 0;
        for (int i = 0; i < nums.size(); i ++){
            ans = max(ans,dp[i]);
        }
        return ans;
    }
};

• Java岛冒险记【从小白到大佬之路】
  
• LeetCode每日一题–进击大厂
• 算法
• C/C++
• Go语言核心编程
• 数据结构