您现在的位置是：首页 >其他 >二叉树OJ题(C++实现)网站首页其他

1.二叉树创建字符串

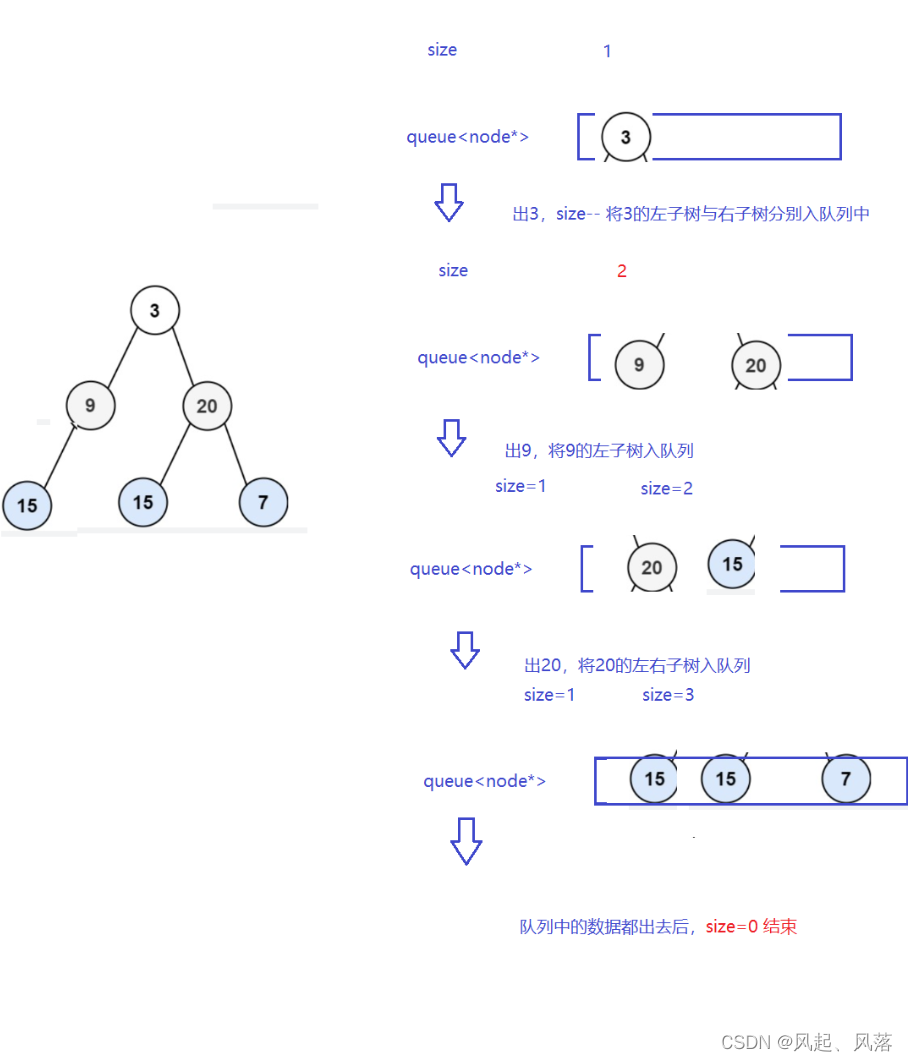
二叉树的层序遍历 OJ连接

主要思路是借助一个队列，将每一层的数据以size统计，当size为0时说明该层数据已经输入完，将这一层的数据传入vector中，再通过push_back 传入 vector< vector< int >中

class Solution {
public:
   
    string tree2str(TreeNode* root) {
      
        if(root==NULL)
        {
            return "";
        }
         string s;
        //to_string 将任意类型转换为字符串
         s=to_string(root->val);
         //只有左右子树都为空时 左子树才不加括号
        if(root->left==NULL&&root->right==NULL)
        {
             //;
        }
        else 
        {
        s+='(';
        s+= tree2str(root->left);
        s+=')';
        }
        //若右子树为空 ，则不加括号
     if(root->right!=NULL)
     {
         s+='(';
         s+=  tree2str(root->right);
         s+=')';
     }
        return s;
    }
};

2. 二叉树的最近公共祖先

二叉树的最近公共祖先OJ连接

共分为三种情况

第一种情况

寻找节点7与0的公共祖先为 根节点3
节点7在根的左子树，而节点0在根的右子树

若一个在根的左子树，一个在根的右子树 ， 则根就为公共祖先

第二种情况
以左子树为例

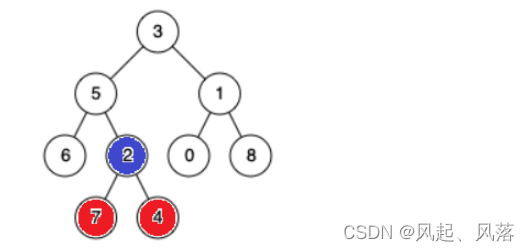
节点7与节点4属于根的左子树
节点7与节点4的最近公共祖先为 他们共同的父节点2

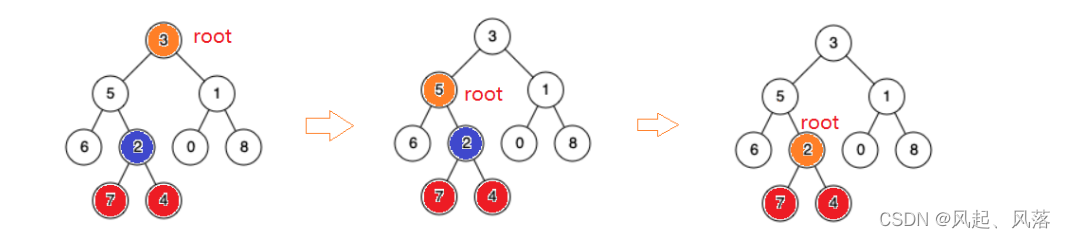
若两个节点都在根的左子树，则递归根的左子树的节点为根，判断两个节点是否为根的左右子树，直到寻找到

第三种情况

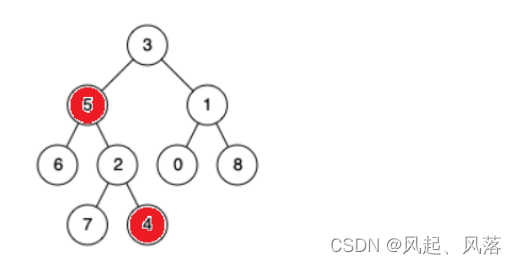
节点5与节点4的最近公共祖先是节点5
节点5与节点4都属于根的左子树
若两个节点都在根的左子树，则递归根的左子树的节点为根，当这个根为两个节点其中一个时，则这个节点就为公共祖先

由于第二种和第三种情况，节点都在左子树上，所以可以看作是一种情况

class Solution {
public:
bool istree(TreeNode*root,TreeNode*x)
{
      if(root==NULL)
      {
          return false;
      }
      if(root==x)
      {
          return true;
      }
      return istree(root->left,x)|| istree(root->right,x);
}
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
          if(root==NULL)
          {
              return NULL;
          }
          //若p/q节点有一个节点为根节点，则最近公共祖先为根节点
          if(p==root||q==root)
          {
              return root;
          }
          
           bool pleft=istree(root->left,p);
           bool pright=!pleft;
           bool qleft=istree(root->left,q);
           bool qright=!qleft;
           //两个节点分别在左右子树上
           if( (pleft&&qright)|| (pright&&qleft))
           {
               return root;
           }
           //两个节点都在根的左子树上，则递归左子树
           else if(pleft&&qleft)
           {
                return lowestCommonAncestor(root->left,p,q);
           }
           //两个节点都在根的右子树上，则递归右子树
           else 
           {
              return lowestCommonAncestor(root->right,p,q);
           }
    }
};

3.二叉搜索树与双向链表

二叉搜索树与双向链表OJ连接

prev节点用于记录cur节点的上一个

当cur节点值为4时，prev=NULL，因为4属于双向链表第一个节点值 所以没必要链接
只需更新prev的值为cur值即可

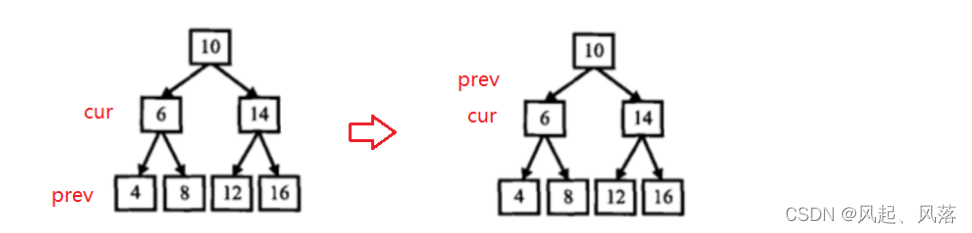
prev值不为空时，将cur节点与prev节点进行连接，并更新prev节点值
prev->right=cur
cur->left=prev

class Solution {
  public:
  void inconvert(TreeNode*cur,TreeNode*&prev)
  //因为prev是要跟着cur进行变化的，所以使用引用
  {
	if(cur==nullptr)
	return ;
	inconvert(cur->left,prev);
	//cur出现的顺序就为中序
	if(prev)
	{
		prev->right=cur;
		cur->left=prev;
	}
	prev=cur;

	inconvert(cur->right,prev);

  }
    TreeNode* Convert(TreeNode* root) {
		TreeNode*prev=nullptr;//记录cur节点的上一个
       inconvert(root,prev);
	    TreeNode*head=root;
		//通过遍历左子树的方式找到第一个节点
		while(head&&head->left)
		{
			head=head->left;
		}
		return head;
    }
};

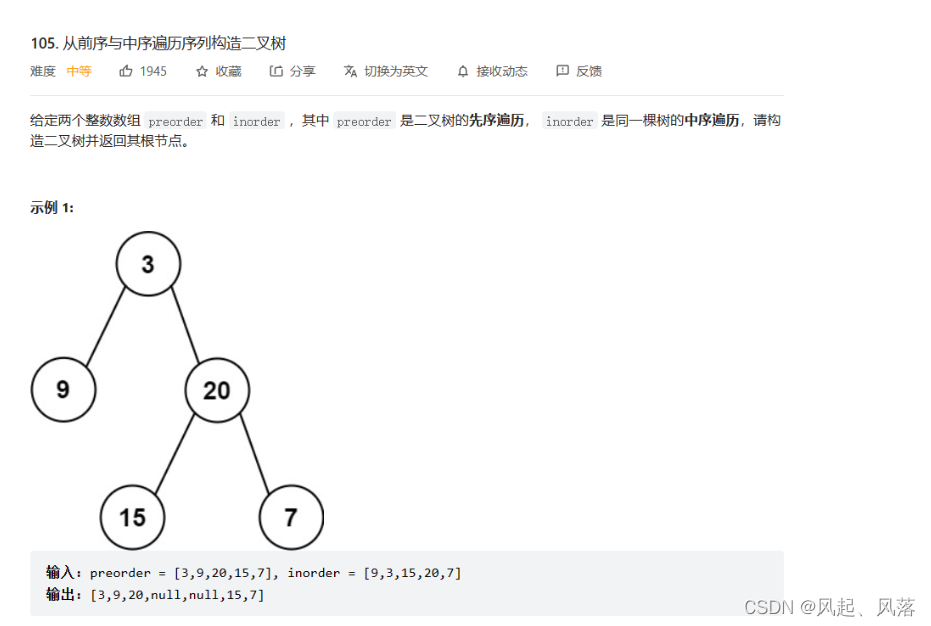
4.从前序与中序遍历序列构造二叉树

从前序与中序遍历序列构造二叉树OJ链接

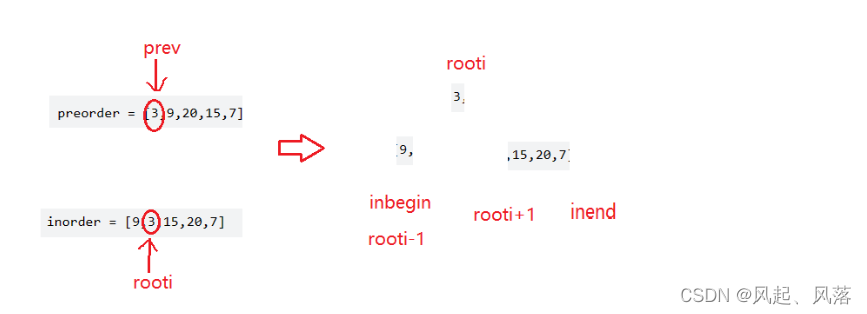
创建root，并确定值为3
在中序数组中寻找 root值为3的节点 ，并标记其下标为rooti
再通过递归的方式分别创建root的left与root的right

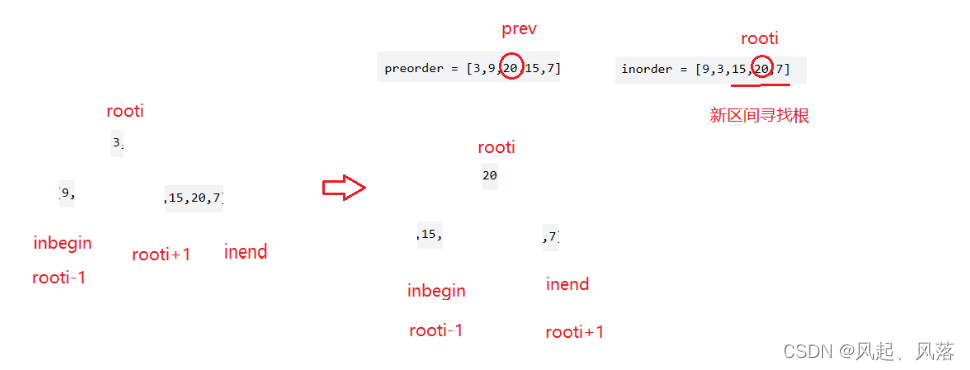
同时每次都需要prev++，来确定新的根，
每次rooti都被赋值为inbegin，是为了中序数组的新区间内寻找到根

递归结束的判断条件

若rooti与inbegin都为数组中第一个数的下标时，
[inbegin, rooti-1] 即 [ 0,-1] 为不存在的区间
所以当 inbegin >inright时，就直接返回

class Solution {
public:
//prev为先序数组的下标
//inbeing与inend为 左右子树分割区间
    TreeNode*istree(vector<int>& preorder, vector<int>& inorder,int &prev,
    int inbegin,int inend)
    {
        //若rooti值与inbegin同时为第一个值，
        //则 [inegin,rooti-1]即 [0 ,-1]会报错
        if(inbegin>inend)
        {
            return nullptr;
        }
        //通过先序创建根节点
        TreeNode*root=new TreeNode();
        root->val=preorder[prev];
        //在中序数组中查找root对应的值
        int rooti=inbegin;
        while(rooti<=inend)
        {
            if(preorder[prev]==inorder[rooti])
            {
                break;
            }
            rooti++;
        }
        prev++;//由于是引用，前序的根也要跟着变化
        //分割左右子树区间
      // [inbegin rooti-1] rooti [rooti+1 inend]
        
      root->left=istree(preorder,inorder,prev,inbegin,rooti-1);
      root->right=istree(preorder,inorder,prev,rooti+1,inend);
      return root;


    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int i=0;
           return  istree(preorder,inorder,i,0,inorder.size()-1);
    }
};