您现在的位置是:首页 >技术教程 >【忍者算法】二叉树展开为链表:空间复杂度O(1)的忍者解法|LeetCode第114题网站首页技术教程
【忍者算法】二叉树展开为链表:空间复杂度O(1)的忍者解法|LeetCode第114题
简介【忍者算法】二叉树展开为链表:空间复杂度O(1)的忍者解法|LeetCode第114题
二叉树展开为链表:空间复杂度O(1)的忍者解法
现实映射:圣诞灯饰的魔法
想象你有一串圣诞树造型的彩灯,每个分岔处都有两个小灯泡。现在你想把它改造成一条直线悬挂在屋檐下。要求所有灯泡必须保持原来的点亮顺序,且只能用右侧的挂钩连接。这就是我们今天要解决的算法问题!
问题描述
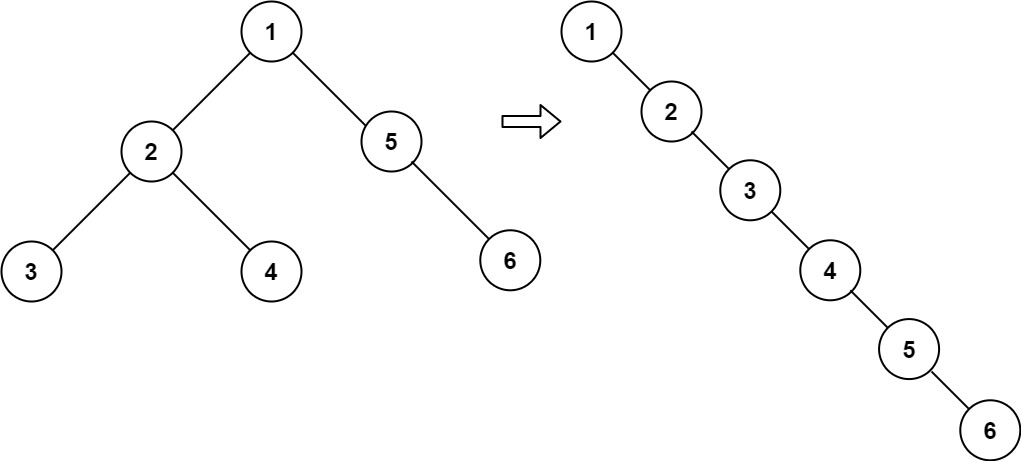
LeetCode第114题要求:给定一个二叉树的根节点,原地将它展开为一个单链表,展开后的链表顺序应与二叉树的前序遍历顺序一致。所有节点的右子指针指向下一个节点,左子指针始终为null。
示例:
输入:
1
/
2 5
/
3 4 6
输出:
1
2
3
4
5
6
直觉解法:前序遍历+重建
最直接的思路就像拆解圣诞灯饰:
- 先完整记录所有灯泡的位置(前序遍历)
- 按照顺序重新组装成链条
Java实现
class Solution {
public void flatten(TreeNode root) {
List<TreeNode> list = new ArrayList<>();
preOrder(root, list);
for (int i = 0; i < list.size()-1; i++) {
TreeNode curr = list.get(i);
curr.left = null;
curr.right = list.get(i+1);
}
}
private void preOrder(TreeNode node, List<TreeNode> list) {
if (node == null) return;
list.add(node);
preOrder(node.left, list);
preOrder(node.right, list);
}
}
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n)(递归栈+列表存储)
忍者解法:原地修改的奥义
真正的忍者不需要额外空间!我们需要在遍历的同时完成链表重组,就像在拆解灯饰的过程中直接重新连接灯泡。
核心思想:寻找前驱节点
在前序遍历中,每个节点的后继其实是其左子树的最右节点。抓住这个规律,我们可以:
-
当前节点有左子树时:
- 找到左子树的最右节点(前驱节点)
- 将当前节点的右子树接到前驱节点的右侧
- 将左子树移到右侧,左指针置空
-
移动到右子节点,重复上述过程
关键步骤演示(以示例为例)
初始状态:
1
/
2 5
/
3 4 6
第1步:处理节点1
左子树最右节点是4
将5接到4的右侧:
1
/
2
/
3 4
5
6
然后左子树移到右侧:
1
2
/
3 4
5
6
第2步:处理节点2
同理操作后变为:
1
2
3
4
5
6
Java实现
class Solution {
public void flatten(TreeNode root) {
TreeNode curr = root;
while (curr != null) {
if (curr.left != null) {
// 找到左子树的最右节点
TreeNode predecessor = curr.left;
while (predecessor.right != null) {
predecessor = predecessor.right;
}
// 重组连接关系
predecessor.right = curr.right;
curr.right = curr.left;
curr.left = null;
}
curr = curr.right;
}
}
}
复杂度分析
时间复杂度:O(n)(每个节点被访问两次)
空间复杂度:O(1)
解法对比
| 方法 | 时间复杂度 | 空间复杂度 | 修改方式 |
|---|---|---|---|
| 前序遍历+重建 | O(n) | O(n) | 非原地 |
| 原地修改法 | O(n) | O(1) | 原地 |
模式总结
这道题体现了两个重要算法思想:
- 莫里斯遍历思想:通过修改树结构来实现O(1)空间遍历
- 链表重组技巧:寻找前驱节点的操作模式
这种模式可以扩展到:
- 将二叉树展开为中序链表
- 将二叉搜索树转换为循环双向链表
- 其他需要原地修改树结构的问题
忍者心法
真正的算法高手,就像优秀的工匠改造灯饰:
- 洞察结构:发现前驱节点的关键作用
- 精细操作:在遍历时同步完成结构调整
- 节约资源:用最少的空间完成最复杂的改造
记住:当题目要求原地修改时,往往需要找到当前结构的某种内在规律,通过巧妙的指针操作来达成目标。
作者:忍者算法
公众号:忍者算法
剑指Offer专项突破版电子书已整理完毕,涵盖所有常考题型及优化解法。关注公众号回复【剑指offer】领取~
风语者!平时喜欢研究各种技术,目前在从事后端开发工作,热爱生活、热爱工作。






 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结