您现在的位置是：首页 >其他 >Pytorch 第三回：二分类逻辑回归模型（上）网站首页其他

Pytorch 第三回：二分类逻辑回归模型（上）

开启深度学习第三回，基于Pytorch的二分类逻辑回归模型。Logistic回归模型虽然名字中带有回归，但是在分类的情况中更为常用。当然，其形式上与多项式回归模型也很相似，也是基于y=ax+b的模型进行训练，变量x也可以是多维的形式。区别是Logistic回归模型会对函数结果y进行逻辑处理，或者说将结果输入给一个sigmoid函数，从而得到一个概率结果。

理论概述

1.sigmoid 函数

其公式如下：

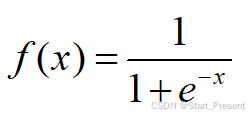
其图形如下图所示，根据图像可以清晰看出，sigmoid函数值分布再0到1之间，输入一个越大的数值，其结果越接近1，输入一个越小的数值，其值约接近0，因此可以将模型转换为一个处理二分类的模型。当然，用sigmoid模型进行分类也有个前提，那就是给定数据是线性可分的，不能是混乱不可分的。

2.前向传播VS反向传播

再接下来的程序当中，需要用到前向传播和反向传播，在这里给大家简答说明以下。

1）前向传播：

前向传播是指神经网络从输入层接收数据开始，通过逐层计算和传递，最终到达输出层的过程。用之前线性回归模型和多项式回归模型用到的方式来说，相当是计算出模型f(x)、更新模型参数(a,b)、计算出当前的函数值y的过程。

2）反向传播：

反向传播是根据损失函数计算梯度，并据此更新网络的权重和偏置，以优化模型性能的过程。回到线性回归模型和多项式回归模型来说，就是做差获得函数的误差，更新参数（a,b）的梯度，接着就是更新模型参数（a，b）。

3.模型优化器

再介绍一个名词，模型优化器。随着深度学习探索的深入，咱们接触的数据量将不断增大，手动更新参数将远远不能满足使用的需求。因此需要借助模型优化器来辅助深度学习的训练。简单来说，优化器是前人封装的好的函数，提供接口给大家使用，进而言之，高级的优化器可以自适应学习率、进行参数更新、增强训练稳定性、应对非凸优化挑战、加速收敛过程等等优点。

4.二分类逻辑回归损失函数

二分类逻辑回归损失函数，推导公式较为繁琐，本人就直接上结论了，若想深入研究，建议查找其他资料，公式如下：

其中，y是真实数值，y’为模型计算的数值。

到此，话不多说，直接上程序。先上程序引用

import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn.functional as F
from torch import nn

一、数据准备

如之前一样，先准备训练的数据。先展示一下需要准备的数据。如下图所示：

如上图所示，我这里准备了100个数据点，分别呈现了红蓝两种颜色。咱们接下要做的就是将这红蓝数据点线性分开。
言归正传，由于此次数据量较多，一个个的将数据写出来不太友好，因此这次采用文件读取的方式获得数据，txt文本数据分享在我的资源中，大家可以去下载。读取数据代码如下：

with open('./point.txt', 'r') as f:
    # 读取数据
    point_list = [i.split('
')[0].split(',') for i in f.readlines()]
    # 将数据以分为三组，分别是x值，y值，类别
    point_data = [(float(i[0]), float(i[1]), float(i[2])) for i in point_list]

获得完数据后，为方便数据分类，接着就是对数据进行归一化处理。代码如下：

x_max = max([i[0] for i in point_data])#找到数据最大值
x_min = min([i[0] for i in point_data])#找到数据最小值
y_max = max([i[1] for i in point_data])
y_min = min([i[1] for i in point_data])
point_data = [((i[0]-x_min) / (x_max-x_min), (i[1]-y_min) / (y_max-y_min), i[2]) for i in point_data]

接着就是将数据转换成训练用的tensor变量。在这里，x代表的是点的位置，y代表的是点的类别（二分类的类别）。

np_data = np.array(point_data, dtype='float32')  # 转换成numpy array
x_data = torch.from_numpy(np_data[:, 0:2])  # 转换成Tensor 
y_data = torch.from_numpy(np_data[:, -1]).unsqueeze(1)  # 转换成Tensor 

如果想如上图一样展示此数据，可以使用如下代码：

point1_x1 = [i[0] for i in point1]
point1_y1 = [i[1] for i in point1]
point2_x2 = [i[0] for i in point2]
point2_y2 = [i[1] for i in point2]

plt.figure('待分类点') # 窗口命名
plt.plot(point1_x1, point1_y1, 'ro', label='Point_1')
plt.plot(point2_x2, point2_y2, 'bo', label='Point_2')
plt.legend( loc='best') # 将图例放到最佳位置
plt.show()

二、模型准备

1.准备logistic 回归模型

模型代码如下，从模型可以看出逻辑回归模型与多项式回归模是相似的。不同的是，这里代码上采用了pytorch提供的函数作为训练模型（引用上要加上import torch.nn.functional as F）。当然函数的输出值表示的是概率值，数值范围在0到1之间。若要转为数据点的类别，还需要进一步处理。

def logistic_regression(x):
    return F.sigmoid(torch.mm(x, a) + b)

2.准备logistic 回归模型参数

在参数准备上，与之前的两回是不同的。这里采用了SGD优化器。代码如下所示，

1） 本次参数的初始化上使用了nn.Parameter()，没有用Variable()函数。不过两者本质是一样的，不同的是Variable()方式是默认不进行梯度运算，而Parameter()则默认进行梯度运算。

2）SGD函数使用也比较简单，其第一个参数是输入参与计算的变量，这里输入的是a，b联合矩阵；第二个参数是学习率，这里设定的是0.5。

torch.manual_seed(2025)# 设定随机种子
# 使用torch.optim 更新参数
a = nn.Parameter(torch.randn(2, 1))
b = nn.Parameter(torch.zeros(1))
optimizer = torch.optim.SGD([a, b], lr=0.5)

3.损失函数定义

代码如下

def Classified_loss(y_pred, y):
    logits = -1*(y * y_pred.clamp(1e-12).log() + (1 - y) * (1 - y_pred).clamp(1e-12).log()).mean()
    return logits

三、模型训练

1、类别确认

在完成函数值的计算后，需要计算类别。在这里需要用到Python中的.ge()函数，相当于对象之间的大于等于（>=）比较操作。具体代码如下所示：

y_pred = logistic_regression(x_data)
mask = y_pred.ge(0.5).float()

2. 精确度

在前两回当中，在迭代训练当中，评判训练结果的方式有误差输出和结果图展示。在本回当中，给大家介绍一个新的评判方式——精确度。这里的精确度指的是预测类别和实际类别的一致性。其代码如下所示：

mask = y_pred.ge(0.5).float()
acc = (mask == y_data).sum().item() / y_data.shape[0]

3. 迭代训练1000，更新参数

接下来就是1000次迭代训练。具体代码如下：

for e in range(1000):
    #前向传播
    y_pred = logistic_regression(x_data)
    loss = Classified_loss(y_pred, y_data)  # 计算loss
    # 反向传播
    optimizer.zero_grad()  # 使用优化器将梯度归零0
    loss.backward()
    optimizer.step()  # 使用优化器更新参数
    # 计算正确率
    mask = y_pred.ge(0.5).float()
    acc = (mask == y_data).sum().item() / y_data.shape[0]
    if (e + 1) % 200 == 0:
        print('epoch:	{},	Loss:	{:.5f},	Acc:	{:.5f}'.format(e + 1, loss, acc))
print('During	Time:	{:.3f}	s'.format(during))

展示输出误差和精确度。

epoch:	200,	Loss:	0.37917,	Acc:	0.92000
epoch:	400,	Loss:	0.30874,	Acc:	0.90000
epoch:	600,	Loss:	0.27802,	Acc:	0.90000
epoch:	800,	Loss:	0.26062,	Acc:	0.90000
epoch:	1000,	Loss:	0.24937,	Acc:	0.89000

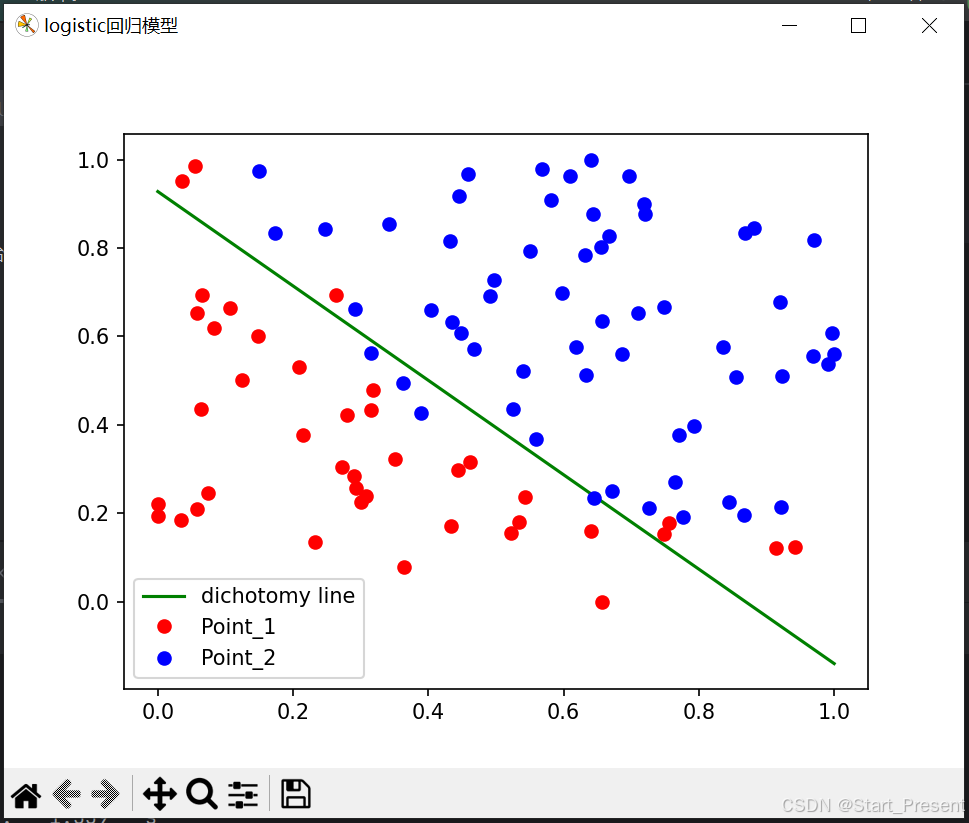
4. 结果展示图

小结

1、数据准备

采用文件读取的方式获得数据点。自变量x是两维，即两轴位置坐标。

2、模型准备

采用pytorch自带的函数搭建logisti回归模型，Parameter()初始化参数（a，b），并引入SGD优化器进行损失计算

2、模型训练

训练评定指标增加正确率的计算，迭代训练1000次。从展示图中可以看出，红蓝两类点大致上可以通过此直线划分出来。