您现在的位置是：首页 >技术教程 >最伟大的算法之一，快速傅立叶变换和FFT算法网站首页技术教程

介绍傅立叶变换的基本概念：傅立叶变换（Fourier Transform）是一个数学工具，用来分析信号的频谱，即将信号从时域转换到频域。

提到傅立叶变换在信号处理、图像分析、音频处理等领域的重要应用。

引出快速傅立叶变换（FFT）作为傅立叶变换的一种高效计算方法，它使得计算速度大大提升，成为现代计算机科学和工程中一个基础而关键的算法。

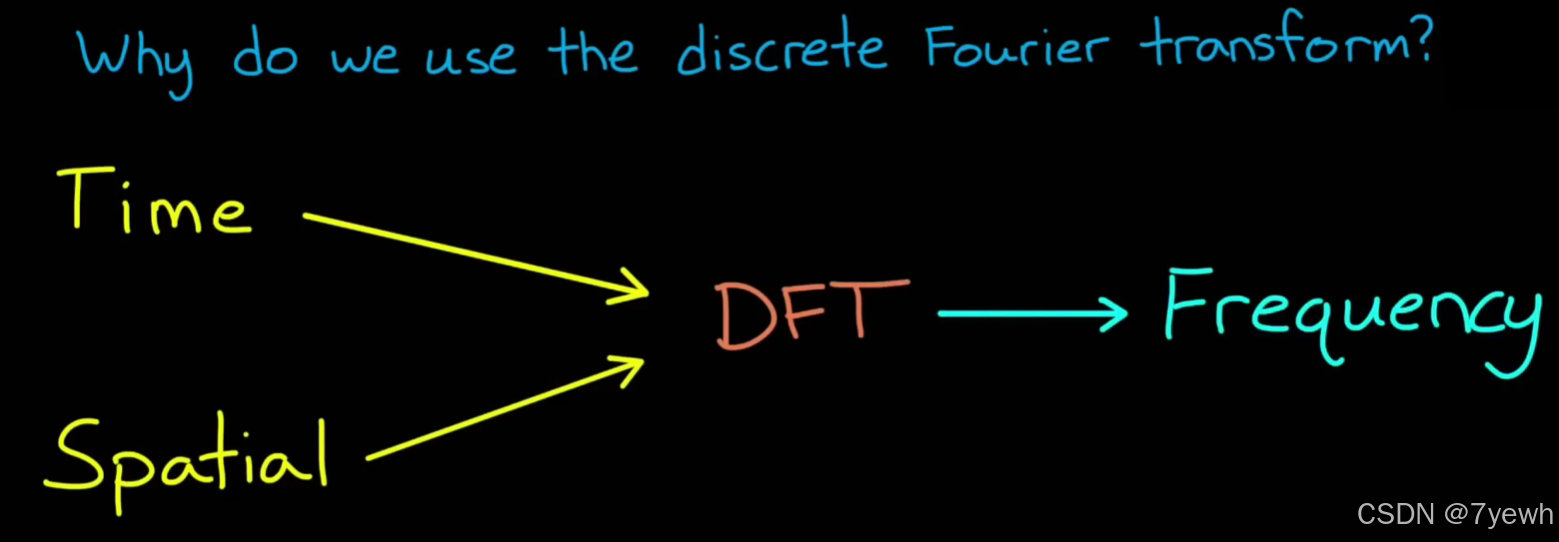
FFT（Fast Fourier Transform，快速傅立叶变换）是一种高效计算离散傅立叶变换（DFT）的方法。傅立叶变换是一种数学工具，它能够将一个信号从时域（或空间域）转换到频域，揭示信号的频谱成分。

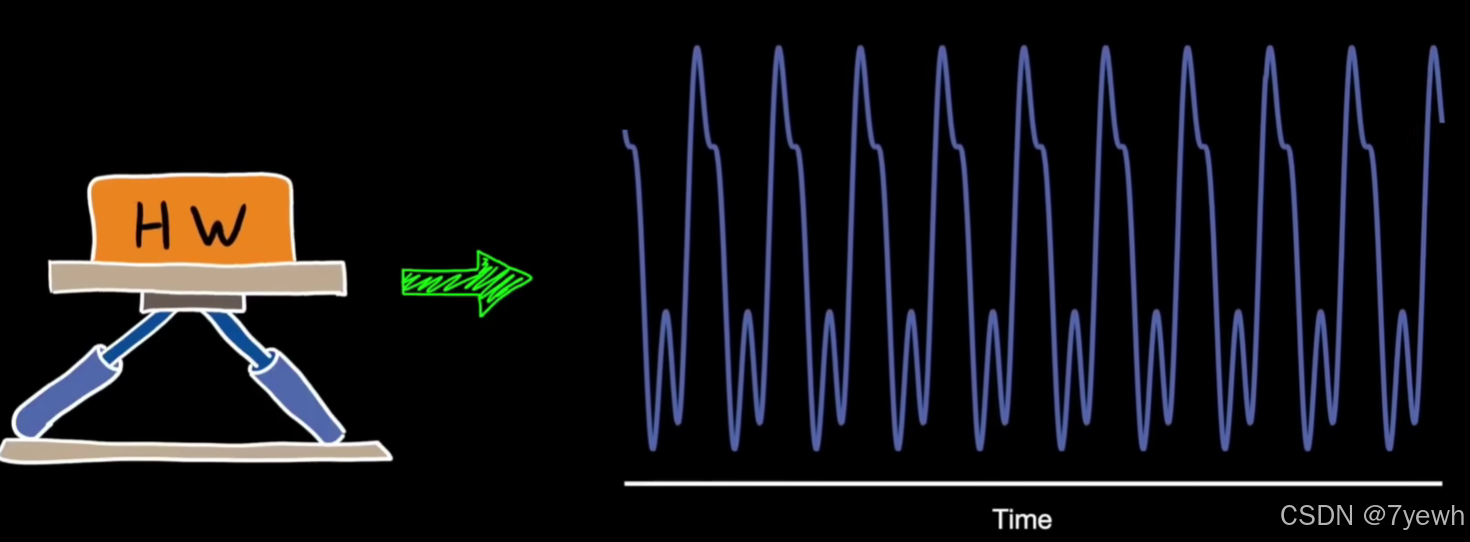
1. 傅立叶变换

首先，傅立叶变换的目标是将一个信号分解为一系列正弦波（不同频率、幅度和相位）。这种变换在分析周期信号时特别有用，比如音频信号、图像数据等。

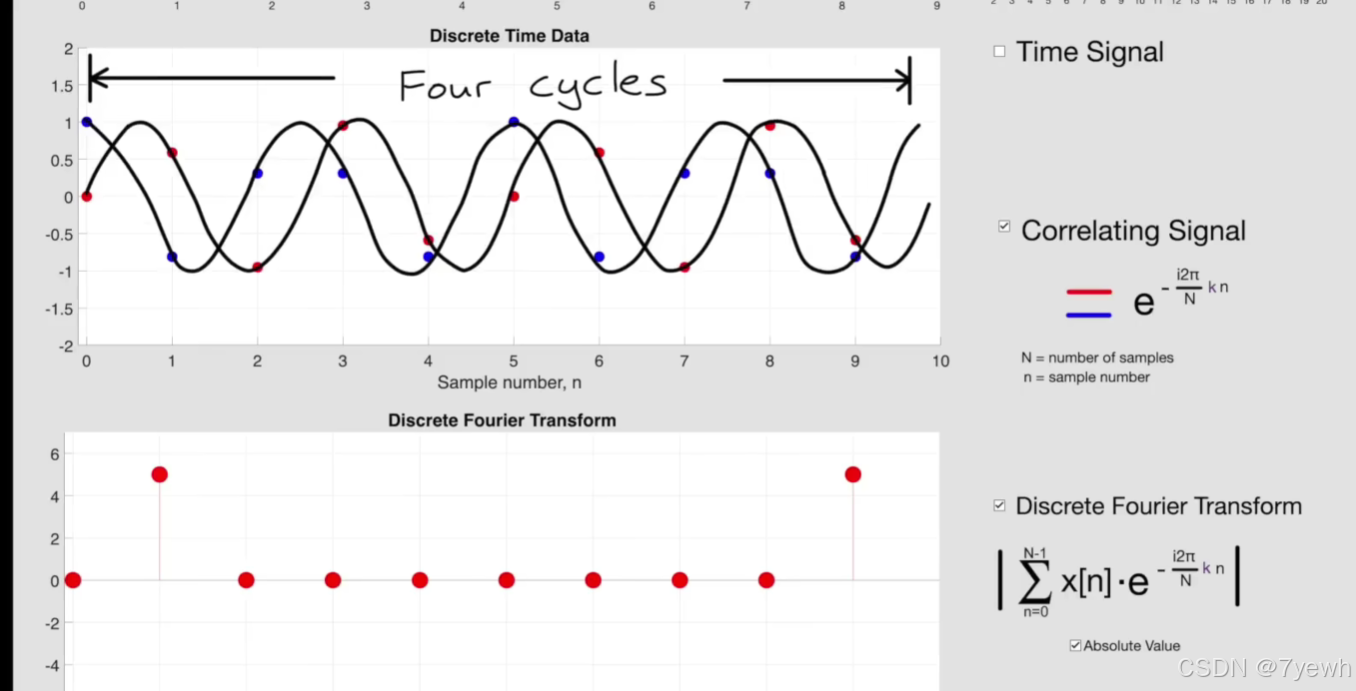
离散傅立叶变换（DFT） 是傅立叶变换在离散数据（数字信号）上的应用，它的定义是：将一个长度为 NNN 的信号序列 x0,x1,…,xN−1x_0, x_1, dots, x_{N-1}x0​,x1​,…,xN−1​ 转换为频域表示的一个长度为 NNN 的复数序列。

其公式为：

Xk=∑n=0N−1xn⋅e−i2πkn/N,k=0,1,…,N−1X_k = sum_{n=0}^{N-1} x_n cdot e^{-i 2pi kn / N}, quad k = 0, 1, dots, N-1Xk​=n=0∑N−1​xn​⋅e−i2πkn/N,k=0,1,…,N−1

这里，XkX_kXk​ 是频域中的第 kkk 个频率分量，xnx_nxn​ 是时域中的信号样本，NNN 是信号的长度。

然而，直接计算 DFT 的方式需要 O(N2)O(N^2)O(N2) 的计算复杂度，这在数据量大的时候非常耗时。

2. FFT：快速傅立叶变换

FFT 是一种高效计算 DFT 的算法。通过巧妙的数学技巧，FFT 将 DFT 的计算复杂度从 O(N2)O(N^2)O(N2) 降低到 O(Nlog⁡N)O(N log N)O(NlogN)，大大提高了计算效率。

FFT 的核心思想是分治法。它将一个大的 DFT 计算任务分解成多个较小的 DFT 任务，再递归地处理这些小任务。最经典的 FFT 算法是 Cooley-Tukey FFT 算法，它的基本思想是将长度为 NNN 的序列分成两个长度为 N/2N/2N/2 的子序列，然后通过递归的方式继续分解，直到处理到最基本的部分。

3. Cooley-Tukey FFT 算法

Cooley-Tukey 算法是最常见的 FFT 算法，它要求输入的数据长度 NNN 是 2 的幂（即 N=2kN = 2^kN=2k，其中 kkk 是整数）。该算法通过递归地将 DFT 分解为更小的 DFT，从而实现高效计算。

算法步骤：将一个长度为 NNN 的序列分成两部分，每部分的长度为 N/2N/2N/2，并且计算这些部分的 DFT。然后，通过“蝶形运算”（Butterfly operation）合并这些子问题的结果，最终得到完整的频域结果。

这种方法大大减少了需要计算的总操作次数，从而使得 FFT 在大规模数据集上的应用变得可行。

在嵌入式系统中，快速傅立叶变换（FFT）算法的应用也非常重要，因为许多嵌入式系统涉及信号处理、音频处理、无线通讯等任务。由于嵌入式设备通常受限于计算资源（如处理器速度、内存等），因此如何高效地实现FFT算法就显得尤为关键。

嵌入式系统中应用FFT的主要场景包括：

音频处理：例如，在音频编码/解码、噪声抑制、回声消除等方面，FFT 可以快速地将时域信号转化为频域信号。无线通信：如OFDM（正交频分复用）技术广泛应用于Wi-Fi、LTE、5G等通信协议中，FFT是关键的技术，用于实现快速的频谱分析。信号分析与处理：嵌入式系统可以通过FFT进行振动分析、设备监控等应用，提取信号中的频率成分。图像处理：FFT 还可以用于图像的频域处理，比如去噪、滤波、边缘检测等。

嵌入式设备通常具备有限的资源，因此在实现 FFT 时需要特别注意以下几个方面：

计算资源限制：嵌入式系统的 CPU 计算能力通常较弱，可能只有低功耗的处理器，这意味着需要优化 FFT 算法来减少计算量。内存限制：嵌入式设备的 RAM 和存储通常较为有限，需要控制内存的使用，避免大规模数据存储或临时缓存。实时性要求：许多嵌入式系统需要实时处理信号，因此 FFT 的执行时间必须尽可能快。

许多嵌入式开发环境和硬件平台提供了优化过的 FFT 库，帮助开发人员节省时间并提高效率：

CMSIS-DSP（ARM）：ARM 提供的 CMSIS-DSP 库包括高效的 FFT 实现，适用于 ARM Cortex-M 系列微控制器。

FFTW：虽然 FFTW 通常用于通用计算平台，但它也提供了一些针对低功耗和嵌入式设备的优化版本。

Intel IPP（Integrated Performance Primitives）：为嵌入式平台提供优化的 FFT 实现，支持 Intel 的处理器。

使用 ARM Cortex-M 系列处理器（如STM32系列）为例，结合 CMSIS-DSP 库，来展示如何高效实现FFT。

我们先定义需要的变量和数组。然后初始化 CMSIS-DSP 库提供的 FFT 模块。

#include "arm_math.h"
#include "stm32f4xx_hal.h"  // STM32的头文件，根据具体的芯片修改

#define FFT_SIZE 1024  // FFT 点数，通常选择2的幂次，比如 1024
#define SAMPLE_RATE 16000  // 假设采样率为 16kHz

float32_t input[FFT_SIZE];  // 输入信号（时域）
float32_t output[FFT_SIZE]; // FFT 输出（频域）
float32_t fft_output[FFT_SIZE]; // 傅立叶变换输出（复数形式）

arm_cfft_radix4_instance_f32 fft_inst;  // FFT 实例
arm_status status;

void SystemClock_Config(void);
void MX_GPIO_Init(void);
void MX_USART2_UART_Init(void);  // 假设使用 USART 进行调试输出

// 假设输入信号是从 ADC 获取的
void acquire_signal(void)
{
    for (int i = 0; i < FFT_SIZE; i++) {
        input[i] = read_adc();  // 从 ADC 读取信号
    }
}

3.2 初始化 FFT 模块

void fft_init(void) {
    // 初始化 FFT 实例
    status = arm_cfft_radix4_init_f32(&fft_inst, FFT_SIZE, 0, 1);  // 0 为正变换，1 为非逆变换
    if (status != ARM_MATH_SUCCESS) {
        // 错误处理
        printf("FFT Initialization Failed!
");
        while (1);
    }
}

执行 FFT 后，得到的是频域信号。这里我们将输入信号转换为复数形式，并进行 FFT。

void perform_fft(void) {
    // 将输入信号从实数转换为复数（需要将输入数据对齐成复数格式）
    for (int i = 0; i < FFT_SIZE; i++) {
        fft_output[2 * i] = input[i];      // 实部
        fft_output[2 * i + 1] = 0.0f;      // 虚部初始化为 0
    }

    // 执行FFT变换
    arm_cfft_radix4_f32(&fft_inst, fft_output);

    // 将结果存入 output 数组
    for (int i = 0; i < FFT_SIZE; i++) {
        output[i] = fft_output[2 * i];  // 只取实部，若需要复数频域数据，可进一步处理
    }
}

为了在嵌入式设备上查看结果，通常使用串口输出（USART）或者显示屏。在这里，我们通过 USART 输出 FFT 的频域数据。

void print_output(void) {
    for (int i = 0; i < FFT_SIZE; i++) {
        printf("Bin %d: %f
", i, output[i]);  // 输出频域的每个 bin
    }
}

将上面的步骤放入主程序的循环中。你可以通过定时器或其他触发机制定期获取 ADC 数据并进行 FFT 计算。

int main(void) {
    // 系统初始化
    HAL_Init();
    SystemClock_Config();
    MX_GPIO_Init();
    MX_USART2_UART_Init();

    // 初始化 FFT
    fft_init();

    while (1) {
        acquire_signal();  // 获取输入信号
        perform_fft();     // 执行 FFT 计算
        print_output();    // 打印频域结果

        HAL_Delay(100);    // 延迟 100ms，调整根据实际需求
    }
}

优化数据存储：在 FFT 计算中，避免额外的数据复制和内存分配，可以使用 原地计算（in-place computation） 方法。

硬件加速：如果使用的嵌入式平台支持硬件加速（如 ARM NEON、DSP），可以利用这些特性加速 FFT 计算。

降低 FFT 点数：根据需求，选择合适的 FFT 点数（例如 512、1024、2048）。较小的点数可以减少计算量，但可能牺牲频率分辨率。