区间动态规划网站首页 学无止境

区间动态规划

Debroon 2023-05-30 20:00:02

简介区间动态规划

区间DP

石子合并：前缀和+递归、动态规划
最长合法子序列
环形石子合并
石子合并 II
城镇国王
超级括号序列
炸弹人

区间DP：

状态：区间左右端点 dp[i][j]
阶段：区间长度
转移：由外到内

石子合并：前缀和+递归、动态规划

最初测试贪心，每次选取最小的组合合并，发现不行。

当没有思路时，以终为始。

从最后一步开始想，考虑合并最后的俩堆石子，一定有一个分界线X。

最后俩堆石子合并 = [第1堆-第X堆] + [第X+1堆-第N堆] + 石子总数

但分界线X在哪里，我们确定不了，贪心算不出，只能枚举一轮找到最小值。

第1堆到第x堆怎么球呢？

寻找分界线m
1-x俩堆石子合并 = [第1堆-第m堆] + [第m+1堆-第x堆] + 1-x的石子总数

依此类推, 直到一堆石子。

for(int i=1; i<=n; i++)
	s[i] = s[i-1] + a[i];         // 前缀和，方便计算[i,j]区间的石子总数

int re( int i, int j )
    if ( i == j )  return 0;      // 只剩下一堆
    int ans = INT_MAX;
    for( int x = i; x < j; x++ )  // 枚举分界线
        ans = min( ans, re(i, x) + re(x+1, j) );
    return ans + s[j] - s[i-1];   // 加上石子总数

添加一个备忘录避免重复计算：

f[256][256];
memset(f, -1, sizeof(f));         // 全部初始化-1

for(int i=1; i<=n; i++)
	s[i] = s[i-1] + a[i];         // 前缀和，方便计算[i,j]区间的石子总数
	
int re( int i, int j )
	if ( f[i][j] != -1 ) return f[i][j];     // 备忘录
    if ( i == j ) return f[i][j] = 0;      
    int ans = INT_MAX;
    for( int x = i; x < j; x++ )             // 枚举分界线
        ans = min( ans, re(i, x) + re(x+1, j) );
    return f[i][j] = ans + s[j] - s[i-1];    // 加上石子总数

这题使用动态规划呢？

问题特征：问总代价最少，求最优解 -> 动态规划的特征。

条件特征：石子合并，线性数组不断缩小的过程 -> 区间动态规划的特征。

按照区间DP定义状态：

dp[i][j]：合并 i-j 区间总代价最少

那 dp[i][j] 从哪里来？

首先思考能不能使用一种最简单的子问题递推关系：看当前子问题和前一个子问题的关系。

如果是一维子问题，就是看 $f (i)$ 和 $f (i - 1)$ 的关系。

如果是二维子问题，则是看 $f (i, j)$ 和 $f (i - 1, j)$ 、 $f (i, j - 1)$ 、 $f (i - 1, j - 1)$ 的关系。

这题子问题是从最小的来，需要逐个比较才能选出最小。

for(int x=i; x<j; x++)
	dp[i][j] = min(dp[i][j]，dp[i][x] + dp[x+1][j] + i-j 的石子总数)

二维计算顺序：

DP 数组计算顺序的基本原则是：当我们计算一个子问题时，它所依赖的其他子问题应该已经计算好了。

DP 数组的有效范围是什么？

base case 和原问题在 DP 数组中在什么位置？

DP 数组的子问题来向是什么？

算例：3、4、11、9

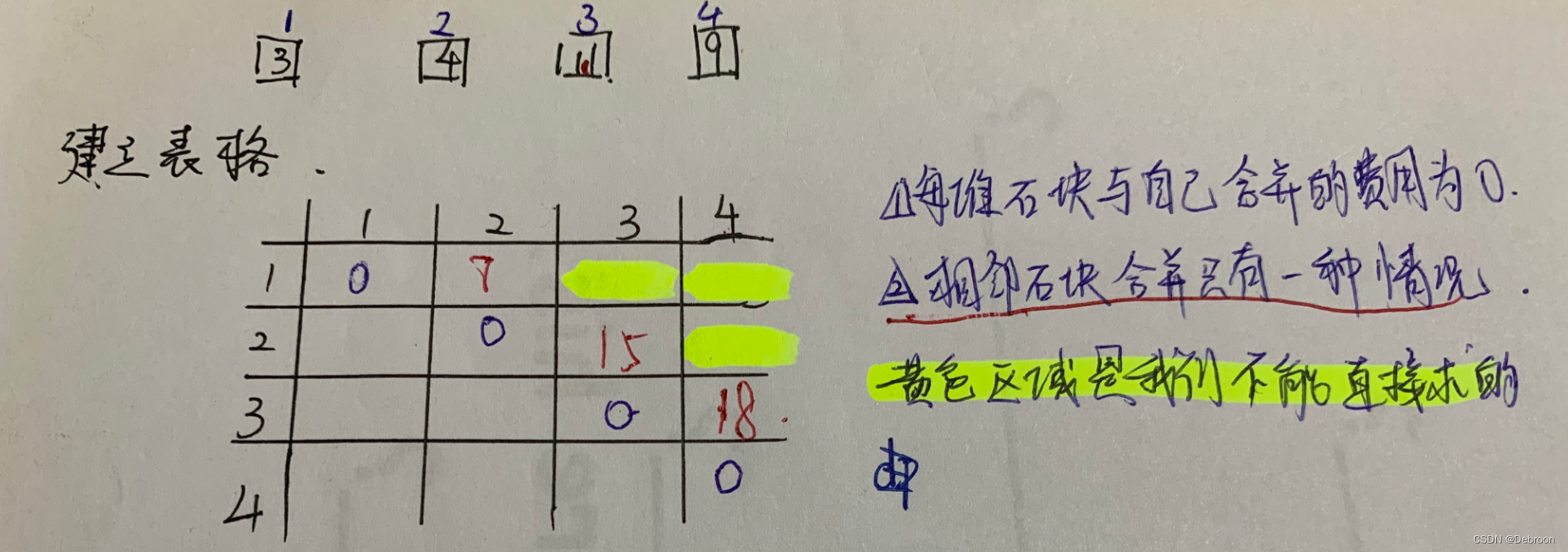
我们算黄色区域：

dp[1][3]=min(dp[1][1]+dp[2][3], dp[1][2]+dp[3][3])+sum[1][3]
dp[2][4]=min(dp[2][3]+dp[4][4], dp[2][2]+dp[3][4])+sum[2][4]
dp[1][4]=min(dp[1][1]+dp[2][4], dp[1][2]+dp[3][4], dp[1][3]+dp[4][4])+sum[1][4]
···
区间长度 = 3：dp[i][i+3]=min(dp[i][i]+dp[i+1][i+3], dp[i][i+1]+dp[i+2][i+3], dp[i][i+2]+dp[i+3][i+3])+sum[i][i+3]

最简单的情况：

for(int len=1; len<=n; len++)           // 区间长度
	for(int i=1; i+len-1<=n; i++)       // 区间起点i
		int j=i+len-1;                  // 区间终点j
		if(len==1)                      // i == j
			f[i][j]=0;
        else
			for(int k=i; k<j; k++)      // 从哪里来
				f[i][j]=min(f[i][j], f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
				
    cout<<f[1][n]<<endl;