1. 977. 有序数组的平方

1.1 题目

977. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序

参考文章：代码随想录 | 977. 有序数组的平方

2.2 思路

使用双指针，创建指针left、right分别指向数组左右两端，创建数组res存储元素的平方结果。
比较指针指向元素的平方大小，将较大的平方结果存入到res数组中，从后向前存，直到两个指针指向同一元素。
时间复杂度O(n)，空间复杂度O(1)。

class Solution {
    public int[] sortedSquares(int[] nums) {
        int left = 0, right = nums.length - 1;
        int[] res = new int[nums.length];
        int index = nums.length - 1;
        while(left <= right){
            int leftSquare = nums[left] * nums[left];
            int rightSquare = nums[right] * nums[right];
            if(leftSquare > rightSquare){ // left指向元素平方较大
                res[index] = leftSquare;
                left++;
            }else if(leftSquare <= rightSquare){ // right指向元素平方较大
                res[index] = rightSquare;
                right--;
            }
            index--;
        }
        return res;
    }
}

2. 209. 长度最小的子数组

2.1 题目

209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

进阶：
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

参考文章：代码随想录 | 209. 长度最小的子数组

2.2 思路

使用滑动窗口。
滑动窗口将窗口的起始位置、终止位置只用一个循环来调整，此时循环的索引一定是窗口的终止位置，才能遍历完整个数组。
实现滑动窗口要确定以下三点：

1. 窗口内是什么
2. 如何移动窗口的起始位置
3. 如何移动窗口的终止位置

此题中，窗口内是元素的和sum；当sum >= target时，窗口的起始位置向右移动；窗口的终止位置即为循环的索引，自动向右移动。

时间复杂度O(n)，空间复杂度O(1)

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left = 0, right = 0;
        int min = Integer.MAX_VALUE;
        int sum = 0;
        while(right < nums.length){ // 滑动窗口右端扩展
            sum += nums[right];
            while(sum >= target){ // 滑动窗口左端收缩
                min = Math.min(min, right - left + 1); // 收缩过程中记录最小值
                sum -= nums[left++];
            }
            right++;
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }
}

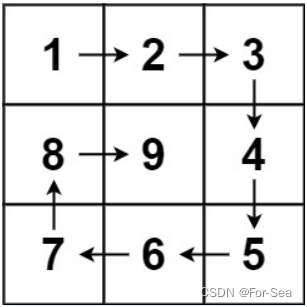
3. 59.螺旋矩阵Ⅱ

3.1 题目

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：
输入：n = 1
输出：[[1]]

提示：
1 <= n <= 20

参考文章：代码随想录 | 59. 螺旋矩阵Ⅱ

3.2 思路

模拟顺时针绕圈的过程，难点在于循环的边界条件。

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] res = new int[n][n];
        int left = 0, right = n - 1;
        int top = 0, buttom = n - 1;
        int num = 1;

        while(left <= right && top <= buttom){
            // 最顶层，从左到右
            for(int i = left; i <= right; i++){
                res[top][i] = num;
                num++;
            }
            ++top;
            // 最右列，从上到下
            for(int i = top; i <= buttom; i++){
                res[i][right] = num;
                num++;
            }
            --right;
            // 最下层，从右到左
            for(int i = right; i >= left; i--){
                res[buttom][i] = num;
                num++;
            }
            --buttom;
            // 最左列，从下到上
            for(int i = buttom; i >= top; i--){
                res[i][left] = num;
                num++;
            }
            ++left;
        }
        return res;
    }
}

4. 存在问题

1. 滑动窗口的窗口如何变动。
2. 螺旋数组如何模拟顺时针旋转，在循环时的边界条件。

5. 今天收获

1. 双指针的思路。
2. 滑动窗口的思路与注意事项。
3. 模拟二维数组顺时针的过程。