20230420 | 977. 有序数组的平方、 209. 长度最小的子数组、59. 螺旋矩阵 II网站首页 技术交流

20230420 | 977. 有序数组的平方、 209. 长度最小的子数组、59. 螺旋矩阵 II

扶我起来继续学习 2023-05-28 16:00:02

简介20230420 | 977. 有序数组的平方、 209. 长度最小的子数组、59. 螺旋矩阵 II

1、977. 有序数组的平方

在这里插入图片描述

方法1：使用暴力法，一遍for，一次排序。这个时间复杂度是 O(n + nlogn)，可以说是O(nlogn)的时间复杂度。

class Solution {
    public int[] sortedSquares(int[] nums) {
        //先计算出平方
        for(int i=0;i<nums.length;i++){
            int sum = nums[i]*nums[i];
            nums[i] = sum;
        }
        //再进行排序
        Arrays.sort(nums);
        return nums;
    }
}

方法2 使用双指针法，定义左右指针，时间复杂度O(n)，实质是花费O(n)的空间记录。因为nums是有序的，大一点的值肯定在左右两边。

 //双指针方法
     public int[] sortedSquares(int[] nums) {
      //记录数组长度
       int n = nums.length-1;
       //定义左右指针
       int leftIndex = 0,rightIndex=n;
       //记录数组，相比暴力，实质就是空间换时间
       int []arr = new int[nums.length];
       while(leftIndex<=rightIndex){
           int x = nums[leftIndex]*nums[leftIndex];
           int y = nums[rightIndex]*nums[rightIndex];
           if(x<=y){
               arr[n--] = y
               rightIndex--;
           }else{
               arr[n--] = x;
               leftIndex++;
           }
       }
       return arr;
    }

2、209. 长度最小的子数组

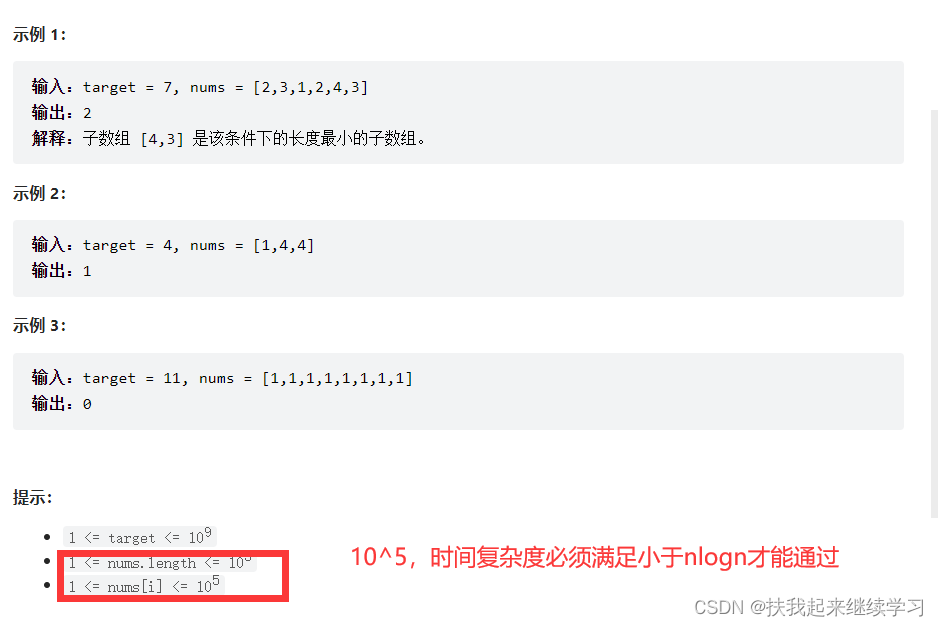
在这里插入图片描述

方法1：使用暴力法，找到最小的子数组，时间复杂度O(n*n)
我把 >=s 看成 =s，
暴力解法已经超时了。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int minVal=Integer.MAX_VALUE;
        int n =nums.length;
        for(int i =0;i<n;i++){
            int sum = 0;
            int index = 0;
            for(int j=i;j<n;j++){
                sum+=nums[j];
                index++;
                if(sum >= target){
                    minVal = Math.min(minVal,index); //记录最小的
                }
                //if(target>sum) continue;//后面的值肯定越来越大，剪枝
            }
        }
        return (minVal == Integer.MAX_VALUE)?0:minVal; //排除一个没找到的情况
    }
}
// 2 3 1 2 4 3
// 2 3
// 2 3 1
// 2 3 1 2

方法2：滑动窗口

数组操作中另一个重要的方法：滑动窗口。
所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。
在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。
在本题中实现滑动窗口，主要确定如下三点：
窗口内是什么？
如何移动窗口的起始位置？
如何移动窗口的结束位置？
窗口就是满足其和 ≥ s 的长度最小的连续子数组。
窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。
窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

 public int minSubArrayLen(int target, int[] nums) {
        int minVal=Integer.MAX_VALUE;
        int n =nums.length;
        int left = 0; //滑动窗口起始位置
        int sum = 0;
        for(int right=0;right<n;right++){
            sum+=nums[right];
            while(sum>=target){
               minVal = Math.min(minVal,right-left+1);
                sum -= nums[left]; //收缩左边，即要减去
                left++;  //收缩左边,left右移动
            }
        }
        return (minVal == Integer.MAX_VALUE)?0:minVal;
    }

不要以为for里放一个while就以为是O(n^2)啊，主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。

3、59. 螺旋矩阵 II

在这里插入图片描述

模拟顺时针画矩阵的过程:
填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上
由外向内一圈一圈这么画下去。
可以发现这里的边界条件非常多，在一个循环中，如此多的边界条件，如果不按照固定规则来遍历，那就是一进循环深似海，从此offer是路人。
这里一圈下来，我们要画每四条边，这四条边怎么画，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。
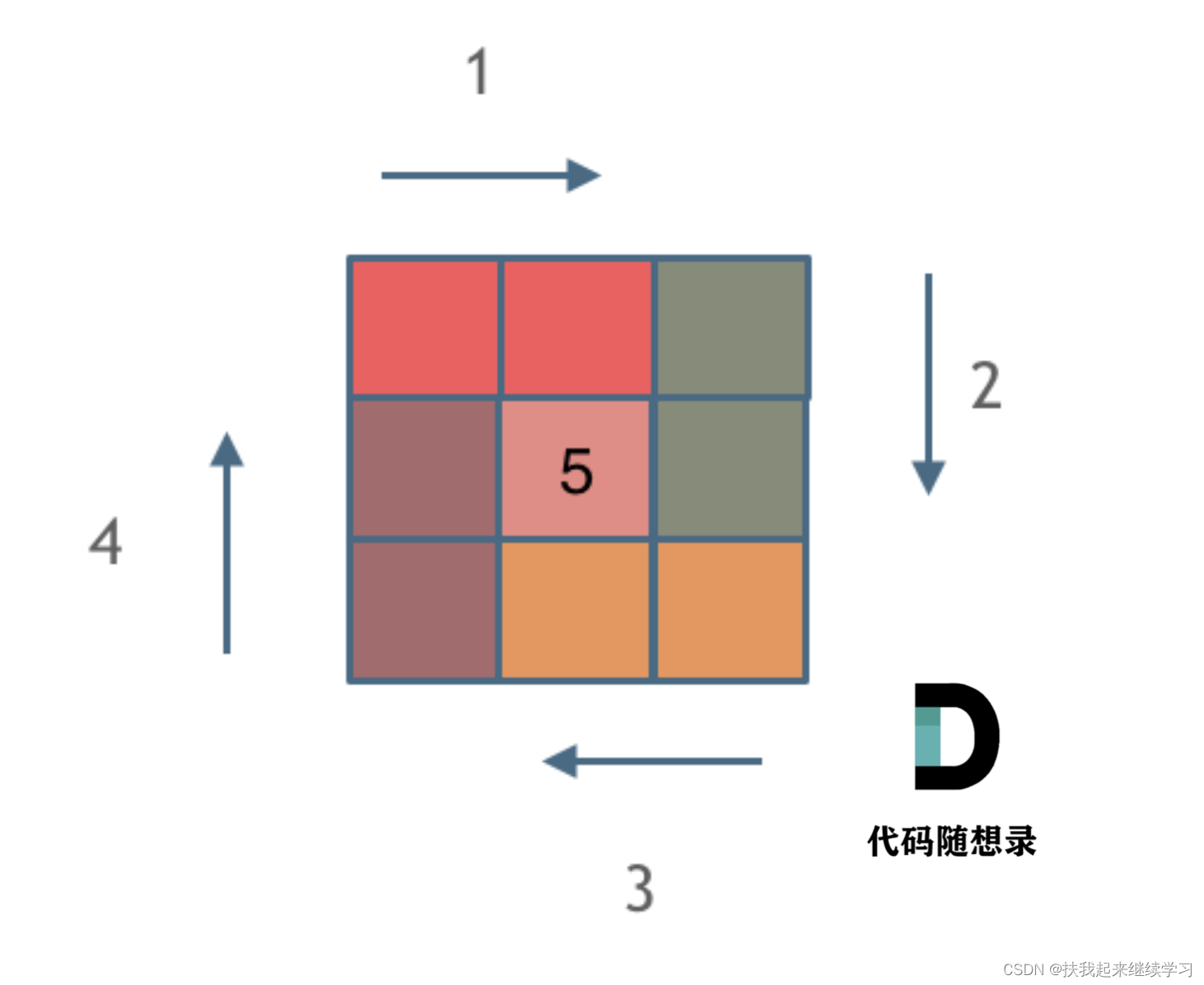
这里每一种颜色，代表一条边，我们遍历的长度，可以看出每一个拐角处的处理规则，拐角处让给新的一条边来继续画。
这也是坚持了每条边左闭右开的原则。

class Solution {
    public int[][] generateMatrix(int n) {
        //3*3
        //从左到右 从上到下 从右到左 从下到上
        int arr[][] = new int[n][n];
        int loop =0;//控制循环次数
        int start = 0 ;//每次循环的开始点(start,start)
        int index =1; //定义要填充的数字
        int i,j; //标志位
        while(loop++<n/2){ //判断边界后，loop从1开始,因为要一圈一圈的走
            //模拟上侧 从左到右
            for(j = start;j<n-loop;j++){
                arr[start][j] = index++;
            }
            //模拟右侧 从上到下
            for(i = start;i<n-loop;i++){
                arr[i][j] = index++;
            }
            //模拟下侧 从右到左
            for(;j>=loop;j--){
                arr[i][j] = index++;
            }
           //模拟左侧 从下到上
            for(;i>=loop;i--){
                arr[i][j] = index++;
            }
             // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            start ++;
        }
        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
       if(n % 2 == 1){
        arr[start][start] =index;
       }
       return arr;
    }
}