今天继续学习动规解决子序列问题。

674.最长连续递增子序列

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。 
示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

思路：

1.昨天还在回忆关于贪心算法中连续子序列的问题，没想到今天第一题就碰上了。相比起Day55的那道递增子序列，本题强调了连续！

2.首先确定dp数组含义，dp[i]表示以下标为i的元素结尾的最长连续递增子序列长度。

3.然后确定递推公式，因为是连续的，因此我们不需要像上一题一样遍历下标i之前的所有元素，只需要看小标为i-1的元素就可以了，因此dp[i] = dp[i - 1] + 1。

4.然后确定初始化，每一个元素至少都包括自己，因此全部初始化为1.

5.最后确定遍历顺序，由递推公式可以看出显然是从前往后遍历。

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        vector<int> dp(nums.size(), 1);
        int result = 1;

        for(int i = 1;i < nums.size(); i++){
            if(nums[i] > nums[i - 1]){
                dp[i] = dp[i - 1] + 1;
            }
            result = max(dp[i], result);
        }

        return result;
    }
};

启发：

1.通过前面这两道题，对于子序列问题有了一个最基本的认识，做题时一定要辨认清楚是连续子序列还是单纯的子序列。

718.最长重复子数组

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

示例 1：

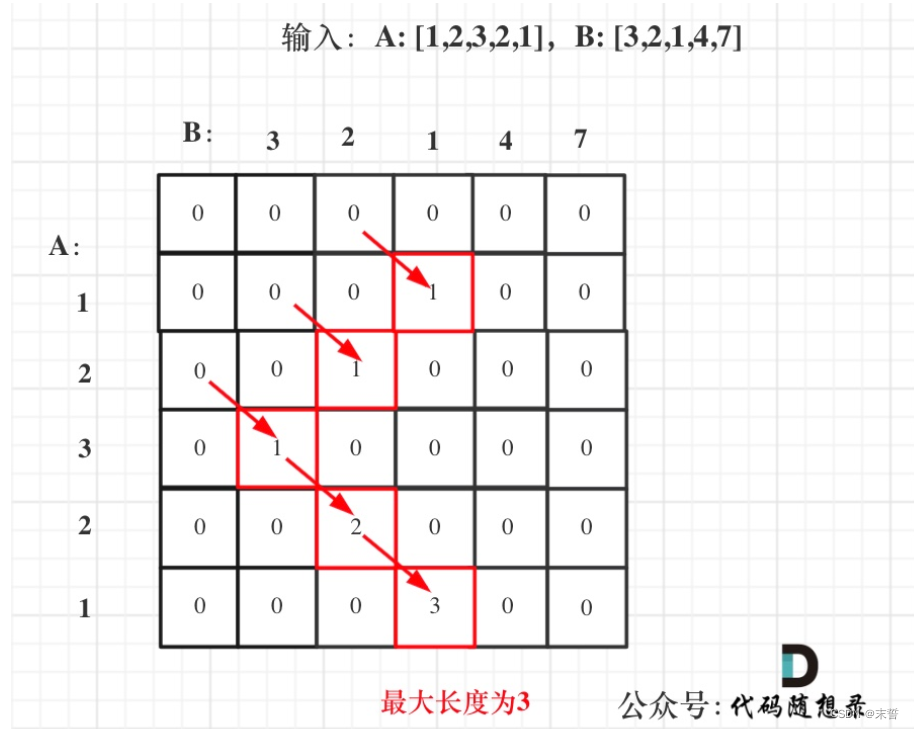
输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。
示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

思路：

1.本题通过示例可以看出要求的实际上和上一道是一样的连续子序列，但本题涉及到对两个数组同时进行比较就稍微有些摸不着头脑了。看了讲解之后才有了一个初步的思路。

2.首先想dp数组含义，本题因为涉及到同时比较两个数组，为了同时记录两个数组的状态我们需要用二维dp数组。dp[i][j]表示以i - 1结尾的nums1，j - 1结尾的nums2，最长重复子数组的长度为dp[i][j]。

3.然后想递推公式，dp[i][j]显然只能通过dp[i - 1][j - 1]推导出来，即dp[i][j] = dp[i - 1][j - 1] + 1。

4.然后想初始化，由递推公式和dp数组含义我们可以看出dp[0][j]和dp[i][0]是没有意义的，但为了方便递推公式我们必须进行初始化，因此将其初始化为0，符合递推公式进行累加。

5.最后想遍历顺序，本题显然需要从前往后遍历。

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        //dp[i][j]表示下标为i - 1结尾的nums1,和下标为j - 1结尾的nums2，最长重复子数组长度为dp[i][j]
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int result = 0;

        for(int i = 1; i <= nums1.size(); i++){
            for(int j = 1; j <= nums2.size(); j++){
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                result = max(result, dp[i][j]);
            }
        }

        return result;
    }
};

启发：

1.本题这种通过二维dp数组分别表示两个数组状态的情况对个人了来说比较少见，尤其是一开始面对该题时几乎没有思路，因此对于本题还需要进一步理解，尤其是dp数组含义和初始化相关。

2.本题的初始化和dp数组含义其实很有讲究。为什么dp[i][j]表示的是以i - 1, j - 1结尾的对应元素，而不是和往常一样表示以i,j结尾的对应元素呢？主要还是为了简化初始化和遍历过程。因为如果按后者赋予dp数组含义，那么第一行和第一列都必须额外进行初始化，即当nums1[i] = nums2[0]时，要将dp[i][0]置为1，当nums2[j] = nums1[0]时同理。

（此处引用代码随想录中的原图和讲解）