( “树” 之 BST) 538. 把二叉搜索树转换为累加树 ——【Leetcode每日一题】网站首页 技术交流

( “树” 之 BST) 538. 把二叉搜索树转换为累加树 ——【Leetcode每日一题】

期望上岸的鱼 2023-05-28 12:00:02

简介( “树” 之 BST) 538. 把二叉搜索树转换为累加树 ——【Leetcode每日一题】

二叉查找树（BST）：根节点大于等于左子树所有节点，小于等于右子树所有节点。
二叉查找树中序遍历有序。

538. 把二叉搜索树转换为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：

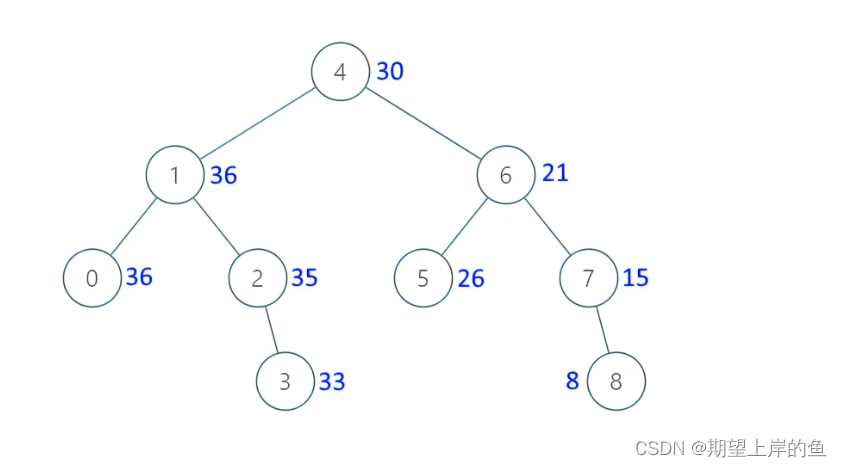
在这里插入图片描述

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 $10^4$ 之间。
每个节点的值介于 -104 和 $10^4$ 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

思路：反序中序遍历

二叉搜索树中序遍历就是有序的，所以中序遍历该树，大于或等于 node.val 的值即是当前节点遍历值及其后面的值。

由于求大于或等于 node.val 的值之和，所以采用右、中、左的遍历顺序，即可得到逆序的序列；
定义一个全局变量sum，记录已经遍历节点的和，当遍历到node节点时，只需再加上sum，即为该节点的替换值。

法一：递归、法二：迭代

略，具体思路请看：94. 二叉树的中序遍历

代码：(Java、C++)

法一：递归
Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        dfs(root);
        return root;
    }
    public void dfs(TreeNode root){
        if(root == null) return;
        if(root.right != null) dfs(root.right);
        root.val += sum;
        sum = root.val;
        if(root.left != null) dfs(root.left);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
        dfs(root);
        return root;
    }
    void dfs(TreeNode* root){
        if(root == nullptr) return;
        if(root->right != nullptr) dfs(root->right);
        root->val += sum;
        sum = root->val;
        if(root->left != nullptr) dfs(root->left);
    }
};

法二：迭代
Java

class Solution {
    public TreeNode convertBST(TreeNode root) {
        Stack<TreeNode> stk = new Stack();
        int sum = 0;
        if(root == null) return root;
        TreeNode cur = root;
        while(cur != null || !stk.isEmpty()){
            while(cur != null){
                stk.push(cur);
                cur = cur.right;
            }
            cur = stk.pop();
            cur.val += sum;
            sum = cur.val;
            cur = cur.left;
        }
        return root;
    }
}

C++

class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        stack<TreeNode*> stk;
        int sum = 0;
        if(root == nullptr) return root;
        TreeNode* cur = root;
        while(cur != nullptr || !stk.empty()){
            while(cur != nullptr){
                stk.push(cur);
                cur = cur->right;
            }
            cur = stk.top();
            stk.pop();
            cur->val += sum;
            sum = cur->val;
            cur = cur->left;
        }
        return root;
    }
};