子集问题网站首页 技术交流

[leetcode算法·回溯]回溯算法秒杀所有排列/组合/子集问题

Captain823Jack 2025-05-13 12:01:03

简介[leetcode算法·回溯]回溯算法秒杀所有排列/组合/子集问题

本文参考labuladong算法笔记[回溯算法秒杀所有排列/组合/子集问题 | labuladong 的算法笔记]

无论是排列、组合还是子集问题，简单说无非就是让你从序列 nums 中以给定规则取若干元素，主要有以下几种变体：

形式一、元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，这也是最基本的形式。

以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该只有 [7]。

形式二、元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次。

以组合为例，如果输入 nums = [2,5,2,1,2]，和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。

形式三、元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次。

以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该有两种 [2,2,3] 和 [7]。

当然，也可以说有第四种形式，即元素可重可复选。但既然元素可复选，那又何必存在重复元素呢？元素去重之后就等同于形式三，所以这种情况不用考虑。

上面用组合问题举的例子，但排列、组合、子集问题都可以有这三种基本形式，所以共有 9 种变化。

除此之外，题目也可以再添加各种限制条件，比如让你求和为 target 且元素个数为 k 的组合，那这么一来又可以衍生出一堆变体，怪不得面试笔试中经常考到排列组合这种基本题型。

但无论形式怎么变化，其本质就是穷举所有解，而这些解呈现树形结构，所以合理使用回溯算法框架，稍改代码框架即可把这些问题一网打尽。

具体来说，你需要先阅读并理解前文回溯算法核心套路，然后记住如下子集问题和排列问题的回溯树，就可以解决所有排列组合子集相关的问题：

为什么只要记住这两种树形结构就能解决所有相关问题呢？

首先，组合问题和子集问题其实是等价的，这个后面会讲；至于之前说的三种变化形式，无非是在这两棵树上剪掉或者增加一些树枝罢了。

那么，接下来我们就开始穷举，把排列/组合/子集问题的 9 种形式都过一遍，学学如何用回溯算法把它们一套带走。

1、元素无重不可复选

1.1 子集问题

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

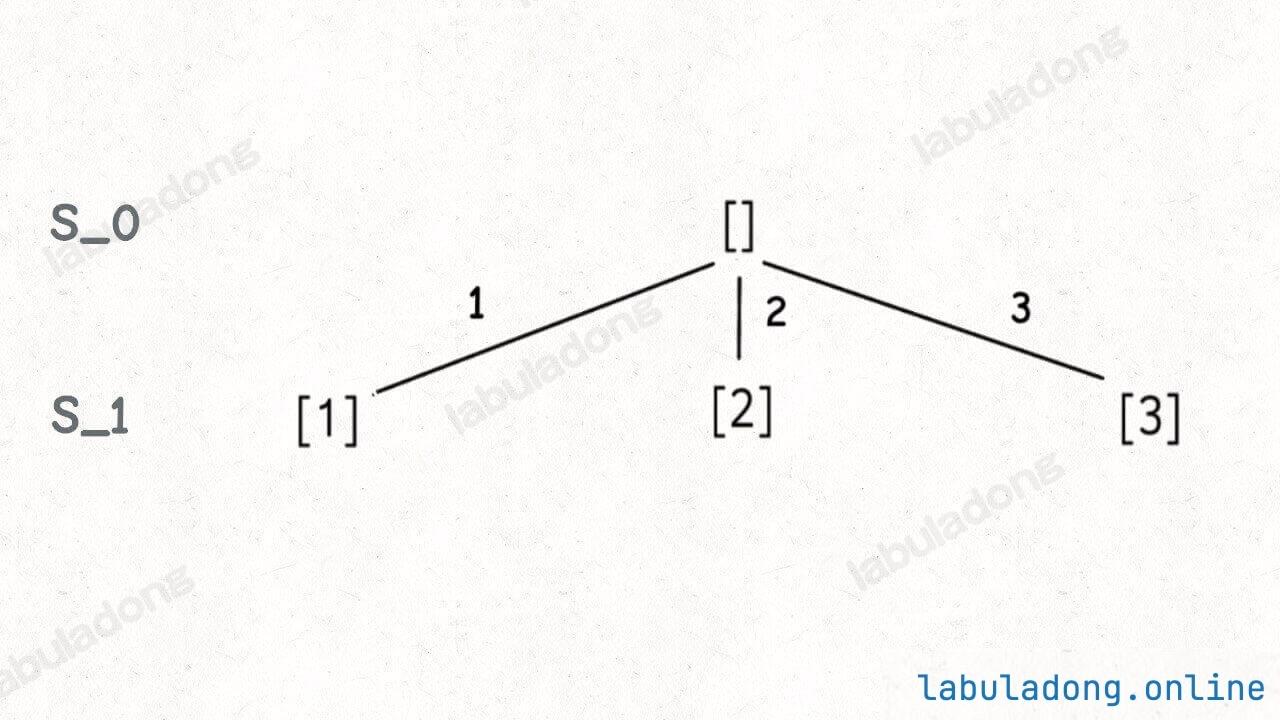
首先，生成元素个数为 0 的子集，即空集 []，为了方便表示，我称之为 S_0。

然后，在 S_0 的基础上生成元素个数为 1 的所有子集，我称为 S_1：

接下来，我们可以在 S_1 的基础上推导出 S_2，即元素个数为 2 的所有子集：

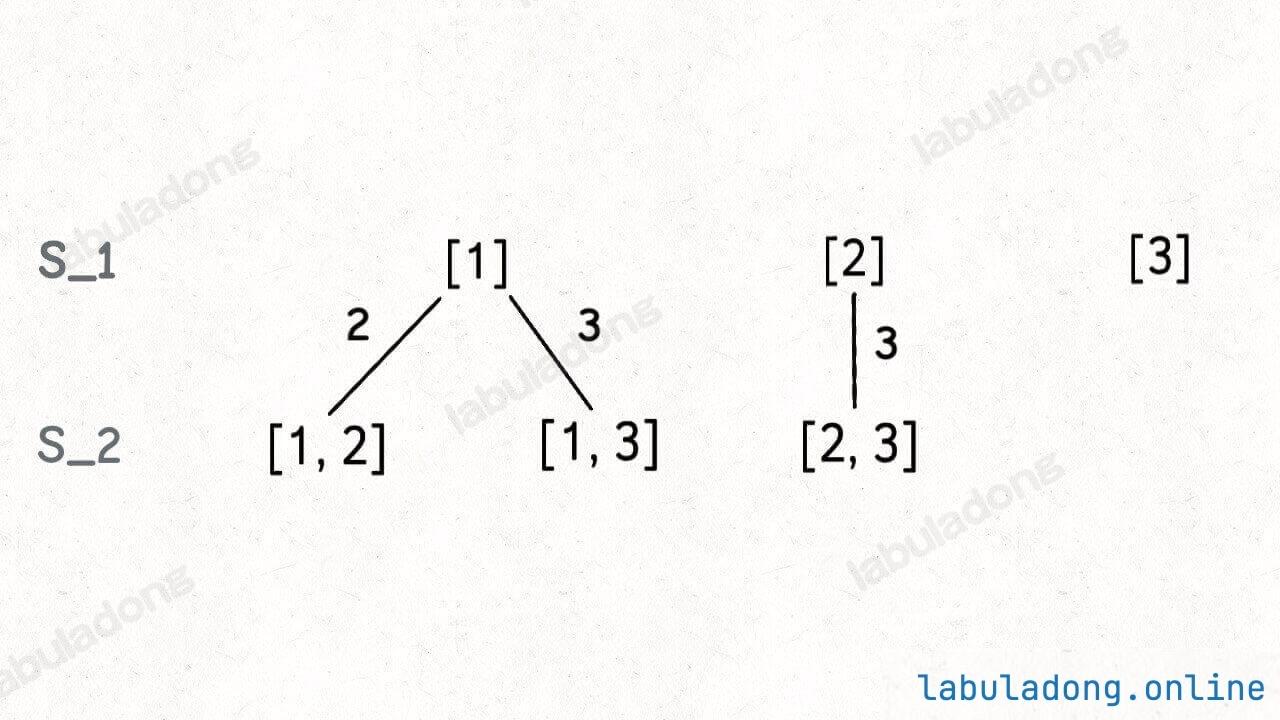
为什么集合 [2] 只需要添加 3，而不添加前面的 1 呢？

因为集合中的元素不用考虑顺序，[1,2,3] 中 2 后面只有 3，如果你添加了前面的 1，那么 [2,1] 会和之前已经生成的子集 [1,2] 重复。

换句话说，我们通过保证元素之间的相对顺序不变来防止出现重复的子集。

接着，我们可以通过 S_2 推出 S_3，实际上 S_3 中只有一个集合 [1,2,3]，它是通过 [1,2] 推出的。

整个推导过程就是这样一棵树：

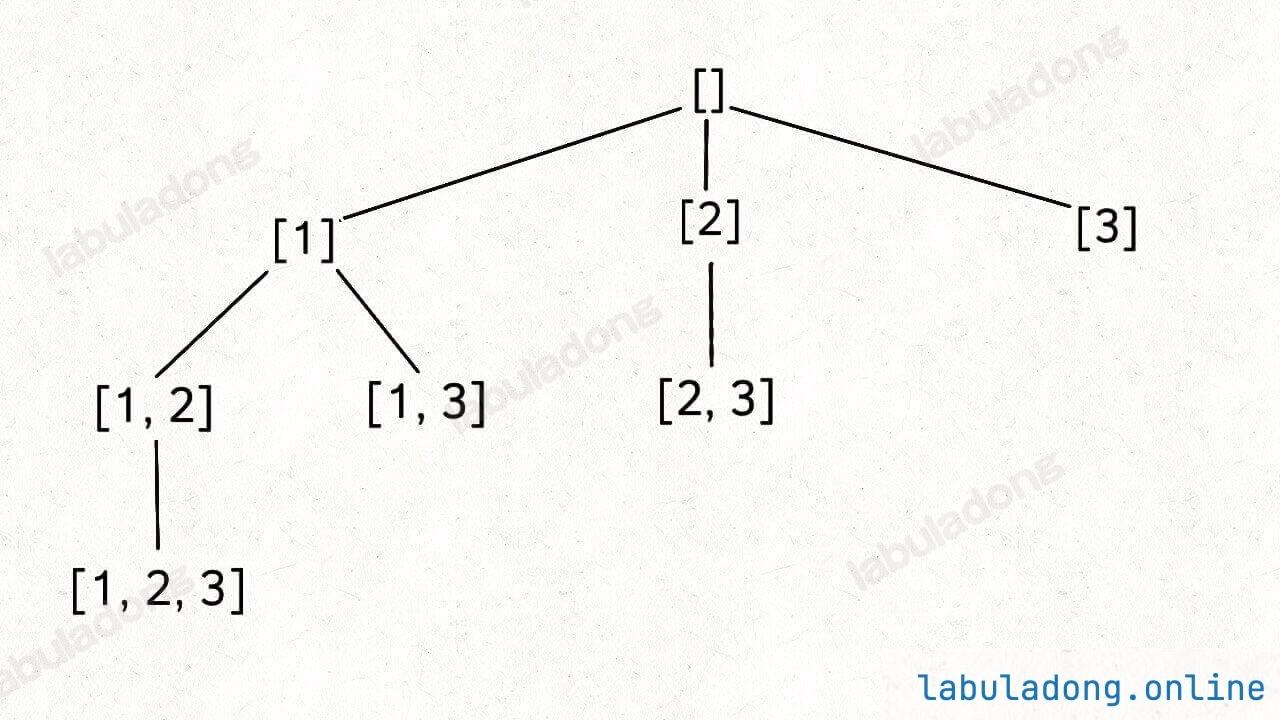
注意这棵树的特性：

如果把根节点作为第 0 层，将每个节点和根节点之间树枝上的元素作为该节点的值，那么第 n 层的所有节点就是大小为 n 的所有子集。

你比如大小为 2 的子集就是这一层节点的值：

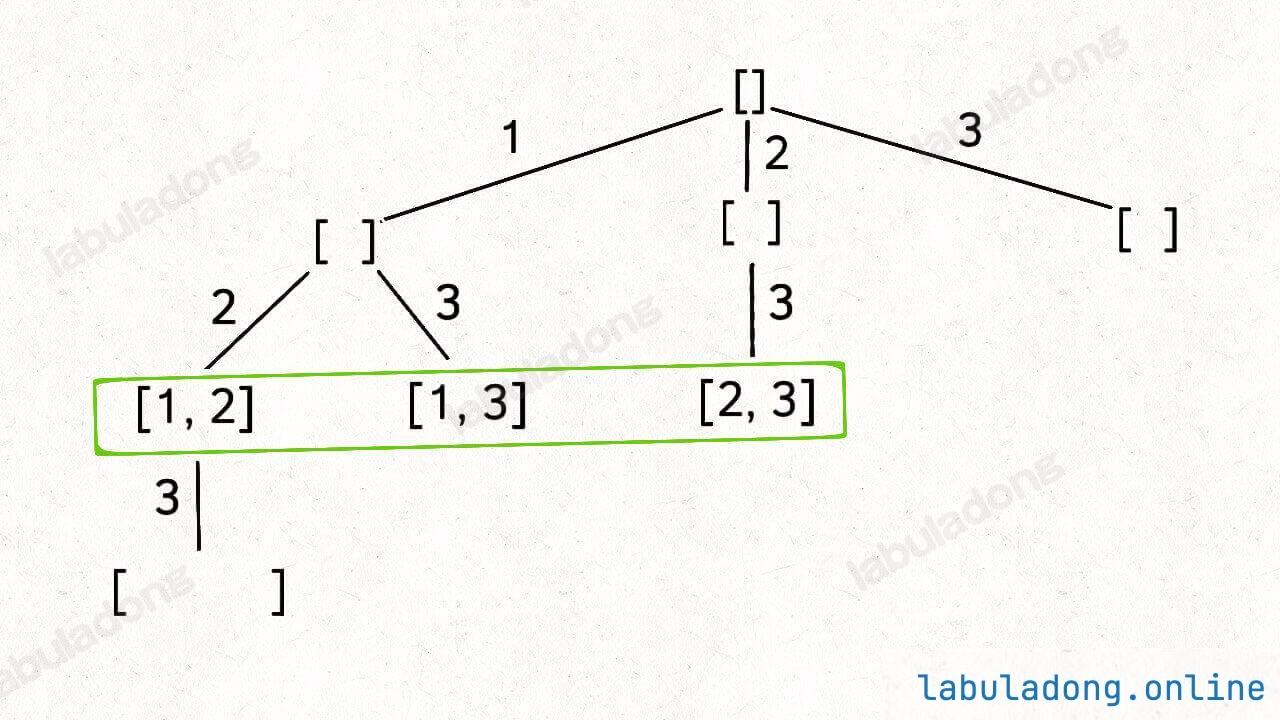
注意，本文之后所说「节点的值」都是指节点和根节点之间树枝上的元素，且将根节点认为是第 0 层。

那么再进一步，如果想计算所有子集，那只要遍历这棵多叉树，把所有节点的值收集起来不就行了？

代码：

class Solution:
    def __init__(self):
        self.res = []
        # 记录回溯算法的递归路径
        self.track = []
    # 主函数
    def subsets(self, nums: List[int]) -> List[List[int]]:
        self.backtrack(nums, 0)
        return self.res
    # 回溯算法核心函数，遍历子集问题的回溯树
    def backtrack(self, nums: List[int], start: int) -> None:
        # 前序位置，每个节点的值都是一个子集
        self.res.append(list(self.track))
        # 回溯算法标准框架
        for i in range(start, len(nums)):
            # 做选择
            self.track.append(nums[i])
            # 通过 start 参数控制树枝的遍历，避免产生重复的子集
            self.backtrack(nums, i + 1)
            # 撤销选择
            self.track.pop()

最后，backtrack 函数开头看似没有 base case，会不会进入无限递归？

其实不会的，当 start == nums.length 时，叶子节点的值会被装入 res，但 for 循环不会执行，也就结束了递归。

1.2 组合问题

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可按任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

如果你能够成功的生成所有无重子集，那么你稍微改改代码就能生成所有无重组合了。

你比如说，让你在 nums = [1,2,3] 中拿 2 个元素形成所有的组合，你怎么做？

稍微想想就会发现，大小为 2 的所有组合，不就是所有大小为 2 的子集嘛。

所以我说组合和子集是一样的：大小为 k 的组合就是大小为 k 的子集。

这是标准的组合问题，但我给你翻译一下就变成子集问题了：

给你输入一个数组 nums = [1,2..,n] 和一个正整数 k，请你生成所有大小为 k 的子集。

还是以 nums = [1,2,3] 为例，刚才让你求所有子集，就是把所有节点的值都收集起来；现在你只需要把第 2 层（根节点视为第 0 层）的节点收集起来，就是大小为 2 的所有组合：

反映到代码上，只需要稍改 base case，控制算法仅仅收集第 k 层节点的值即可。

代码：

class Solution:
    def __init__(self):
        self.res = []
        # 记录回溯算法的递归路径
        self.track = []

    # 主函数
    def combine(self, n: int, k: int) -> List[List[int]]:
        self.backtrack(1, n, k)
        return self.res

    def backtrack(self, start: int, n: int, k: int) -> None:
        # base case
        if k == len(self.track):
            # 遍历到了第 k 层，收集当前节点的值
            self.res.append(self.track.copy())
            return
        
        # 回溯算法标准框架
        for i in range(start, n+1):
            # 选择
            self.track.append(i)
            # 通过 start 参数控制树枝的遍历，避免产生重复的子集
            self.backtrack(i + 1, n, k)
            # 撤销选择
            self.track.pop()

1.3 排列问题

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

刚才讲的组合/子集问题使用 start 变量保证元素 nums[start] 之后只会出现 nums[start+1..] 中的元素，通过固定元素的相对位置保证不出现重复的子集。

但排列问题本身就是让你穷举元素的位置，nums[i] 之后也可以出现 nums[i] 左边的元素，所以之前的那一套玩不转了，需要额外使用 used 数组来标记哪些元素还可以被选择。

标准全排列可以抽象成如下这棵多叉树：

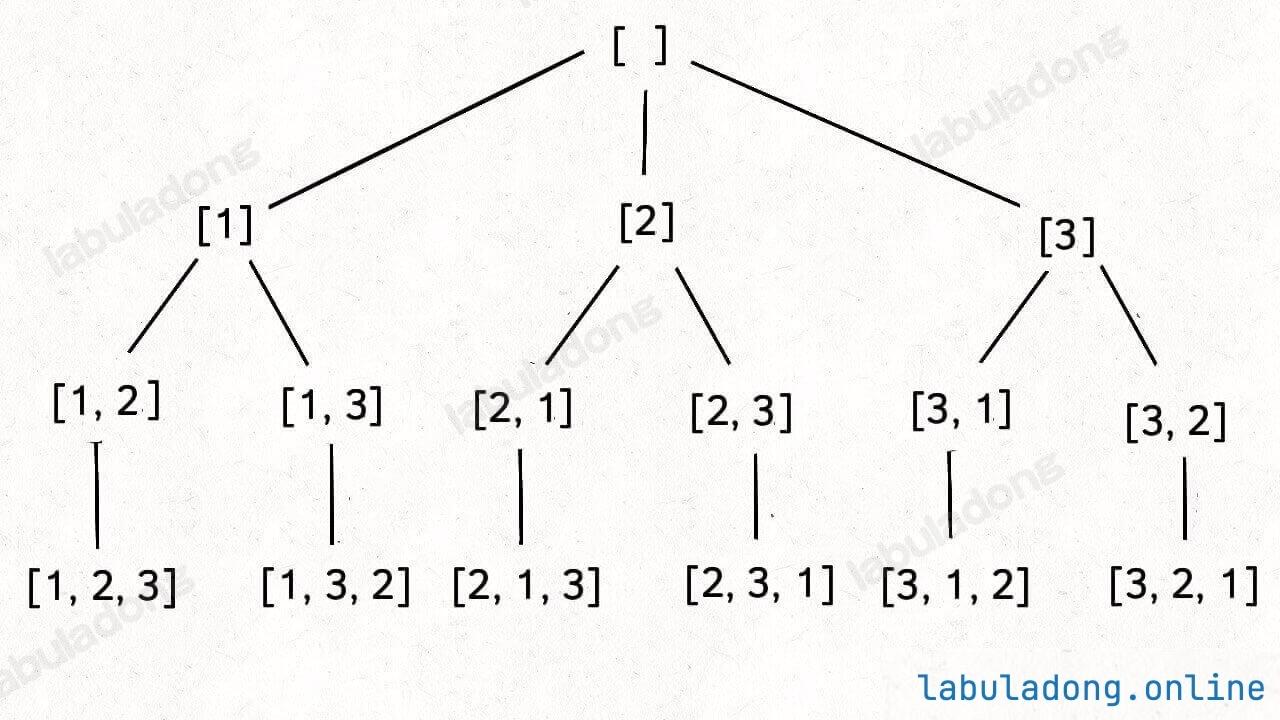
我们用 used 数组标记已经在路径上的元素避免重复选择，然后收集所有叶子节点上的值，就是所有全排列的结果。

代码：

class Solution:
    def __init__(self):
        # 存储所有排列结果的列表
        self.res = []
        # 记录回溯算法的递归路径
        self.track = []
        # track 中的元素会被标记为 true
        self.used = []
    
    # 主函数，输入一组不重复的数字，返回它们的全排列
    def permute(self, nums: List[int]) -> List[List[int]]:
        self.used = [False] * len(nums)
        self.backtrack(nums)
        return self.res
    
    # 回溯算法核心函数
    def backtrack(self, nums: List[int]) -> None:
        # base case，到达叶子节点
        if len(self.track) == len(nums):
            # 收集叶子节点上的值
            self.res.append(self.track[:])
            return
        
        # 回溯算法标准框架
        for i in range(len(nums)):
            # 已经存在 track 中的元素，不能重复选择
            if self.used[i]:
                continue
            # 做选择
            self.used[i] = True
            self.track.append(nums[i])
            # 进入下一层回溯树
            self.backtrack(nums)
            # 取消选择
            self.track.pop()
            self.used[i] = False

但如果题目不让你算全排列，而是让你算元素个数为 k 的排列，怎么算？

也很简单，改下 backtrack 函数的 base case，仅收集第 k 层的节点值即可：

# 回溯算法核心函数
def backtrack(nums: List[int], k: int) -> None:
    # base case，到达第 k 层，收集节点的值
    if len(track) == k:
        # 第 k 层节点的值就是大小为 k 的排列
        res.append(track[:])
        return

    # 回溯算法标准框架
    for i in range(len(nums)):
        # ...
        backtrack(nums, k)
        # ...

2、元素有重不可复选

2.1 子集/组合问题

90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10

当然，按道理说「集合」不应该包含重复元素的，但既然题目这样问了，我们就忽略这个细节吧，仔细思考一下这道题怎么做才是正事。

就以 nums = [1,2,2] 为例，为了区别两个 2 是不同元素，后面我们写作 nums = [1,2,2']。

按照之前的思路画出子集的树形结构，显然，两条值相同的相邻树枝会产生重复：

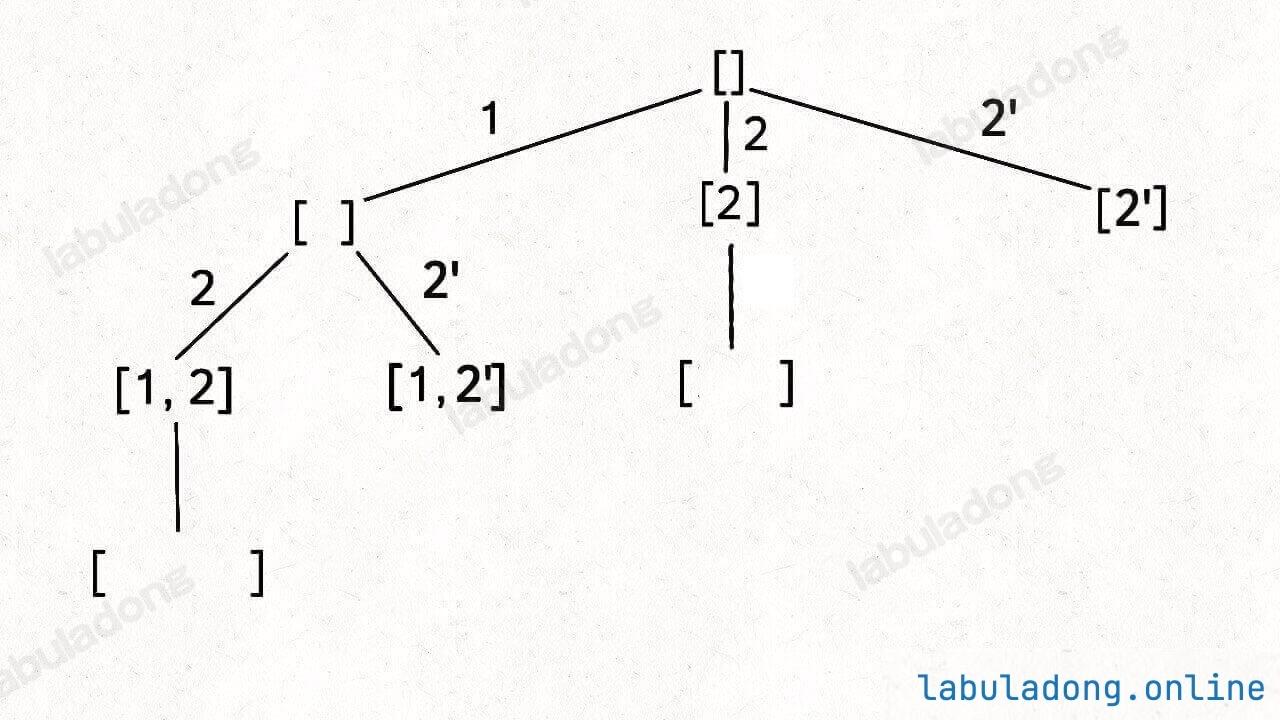
[ [],[1],[2],[2'],[1,2],[1,2'],[2,2'],[1,2,2']]

你可以看到，[2] 和 [1,2] 这两个结果出现了重复，所以我们需要进行剪枝，如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉，不要去遍历：

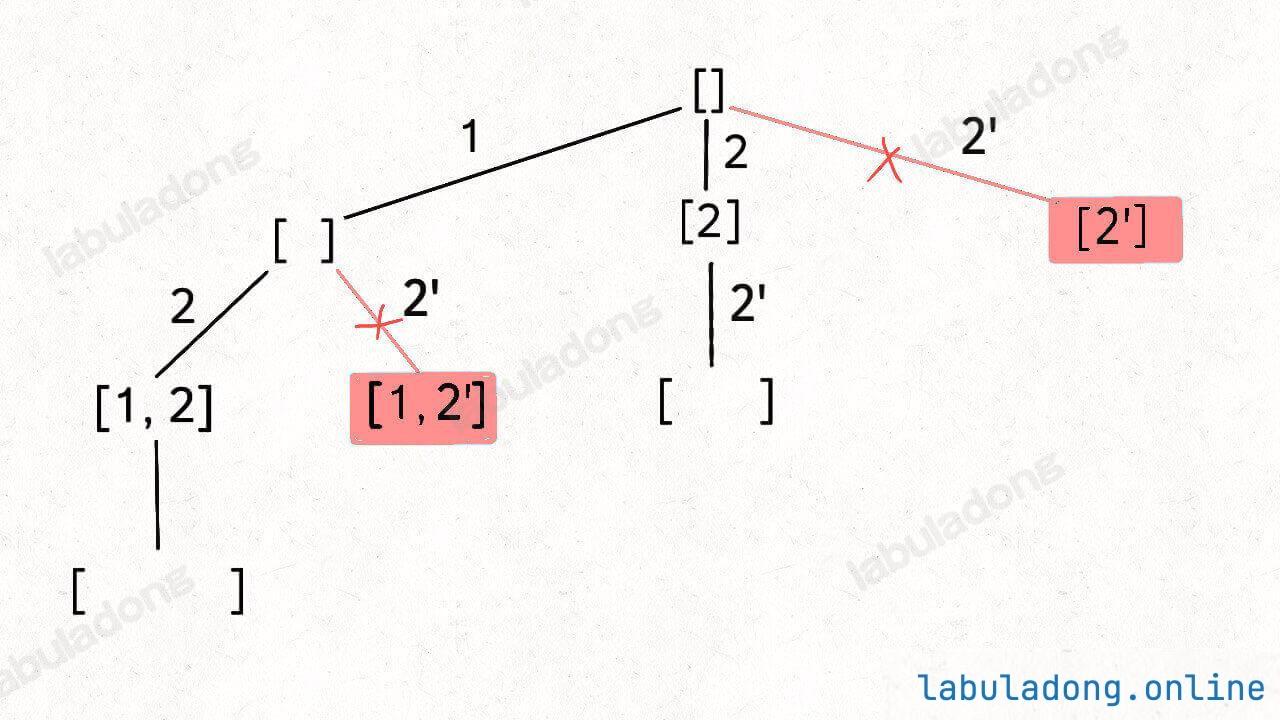
体现在代码上，需要先进行排序，让相同的元素靠在一起，如果发现 nums[i] == nums[i-1]，则跳过。

代码：

class Solution:
    def __init__(self):
        self.res = []
        self.track = []
    
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        # 先排序，让相同的元素靠在一起
        nums.sort()
        self.backtrack(nums, 0)
        return self.res
    
    def backtrack(self, nums: List[int], start: int) -> None:
        # 前序位置，每个节点的值都是一个子集
        self.res.append(self.track[:])
        
        for i in range(start, len(nums)):
            # 剪枝逻辑，值相同的相邻树枝，只遍历第一条
            if i > start and nums[i] == nums[i - 1]:
                continue
            self.track.append(nums[i])
            self.backtrack(nums, i + 1)
            self.track.pop()

40. 组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[[1,1,6], [1,2,5], [1,7], [2,6]]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[[1,2,2],[5]]

提示:

1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30

我们说了组合问题和子集问题是等价的。

对比子集问题的解法，只要额外用一个 trackSum 变量记录回溯路径上的元素和，然后将 base case 改一改即可解决这道题。

代码：

class Solution:
    def __init__(self):
        self.res = []
        # 记录回溯的路径
        self.track = []
        # 记录 track 中的元素之和
        self.trackSum = 0
    
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        if not candidates:
            return self.res
        # 先排序，让相同的元素靠在一起
        candidates.sort()
        self.backtrack(candidates, 0, target)
        return self.res
    
    # 回溯算法主函数
    def backtrack(self, nums: List[int], start: int, target: int):
        # base case，达到目标和，找到符合条件的组合
        if self.trackSum == target:
            self.res.append(self.track[:])
            return
        # base case，超过目标和，直接结束
        if self.trackSum > target:
            return
        
        # 回溯算法标准框架
        for i in range(start, len(nums)):
            # 剪枝逻辑，值相同的树枝，只遍历第一条
            if i > start and nums[i] == nums[i - 1]:
                continue
            # 做选择
            self.track.append(nums[i])
            self.trackSum += nums[i]
            # 递归遍历下一层回溯树
            self.backtrack(nums, i + 1, target)
            # 撤销选择
            self.track.pop()
            self.trackSum -= nums[i]

2.2 排列问题

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8
-10 <= nums[i] <= 10

代码：

class Solution:
    def __init__(self):
        self.res = []
        self.track = []
        self.used = []
    
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        # 先排序，让相同的元素靠在一起
        nums.sort()
        self.used = [False] * len(nums)
        self.backtrack(nums)
        return self.res
    
    def backtrack(self, nums: List[int]) -> None:
        if len(self.track) == len(nums):
            self.res.append(self.track[:])
            return

        for i in range(len(nums)):
            if self.used[i]:
                continue
            # 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
            if i > 0 and nums[i] == nums[i - 1] and not self.used[i - 1]:
                continue
            self.track.append(nums[i])
            self.used[i] = True
            self.backtrack(nums)
            self.track.pop()
            self.used[i] = False

你对比一下之前的标准全排列解法代码，这段解法代码只有两处不同：

1、对 nums 进行了排序。

2、添加了一句额外的剪枝逻辑。

但是注意排列问题的剪枝逻辑，和子集/组合问题的剪枝逻辑略有不同：新增了 !used[i - 1] 的逻辑判断。

假设输入为 nums = [1,2,2']，标准的全排列算法会得出如下答案：

[
    [1,2,2'],[1,2',2],
    [2,1,2'],[2,2',1],
    [2',1,2],[2',2,1]
]

显然，这个结果存在重复，比如 [1,2,2'] 和 [1,2',2] 应该只被算作同一个排列，但被算作了两个不同的排列。

所以现在的关键在于，如何设计剪枝逻辑，把这种重复去除掉？

答案是，保证相同元素在排列中的相对位置保持不变。

比如说 nums = [1,2,2'] 这个例子，我保持排列中 2 一直在 2' 前面。

这样的话，你从上面 6 个排列中只能挑出 3 个排列符合这个条件：

[ [1,2,2'],[2,1,2'],[2,2',1] ]

这也就是正确答案。

进一步，如果 nums = [1,2,2',2'']，我只要保证重复元素 2 的相对位置固定，比如说 2 -> 2' -> 2''，也可以得到无重复的全排列结果。

仔细思考，应该很容易明白其中的原理：

标准全排列算法之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的；而如果固定相同元素形成的序列顺序，当然就避免了重复。

所以当同一层前面的数和自身相等，且为False时，如果自身先加入path则破坏了这种相对顺序。

那么反映到代码上，你注意看这个剪枝逻辑：

// 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
    // 如果前面的相邻相等元素没有用过，则跳过
    continue;
}
// 选择 nums[i]

当出现重复元素时，比如输入 nums = [1,2,2',2'']，2' 只有在 2 已经被使用的情况下才会被选择，同理，2'' 只有在 2' 已经被使用的情况下才会被选择，这就保证了相同元素在排列中的相对位置保证固定。

这里拓展一下，如果你把上述剪枝逻辑中的 !used[i - 1] 改成 used[i - 1]，其实也可以通过所有测试用例，但效率会有所下降，这是为什么呢？

之所以这样修改不会产生错误，是因为这种写法相当于维护了 2'' -> 2' -> 2 的相对顺序，最终也可以实现去重的效果。

但为什么这样写效率会下降呢？因为这个写法剪掉的树枝不够多。

比如输入 nums = [2,2',2'']，产生的回溯树如下：

如果用绿色树枝代表 backtrack 函数遍历过的路径，红色树枝代表剪枝逻辑的触发，那么 !used[i - 1] 这种剪枝逻辑得到的回溯树长这样：

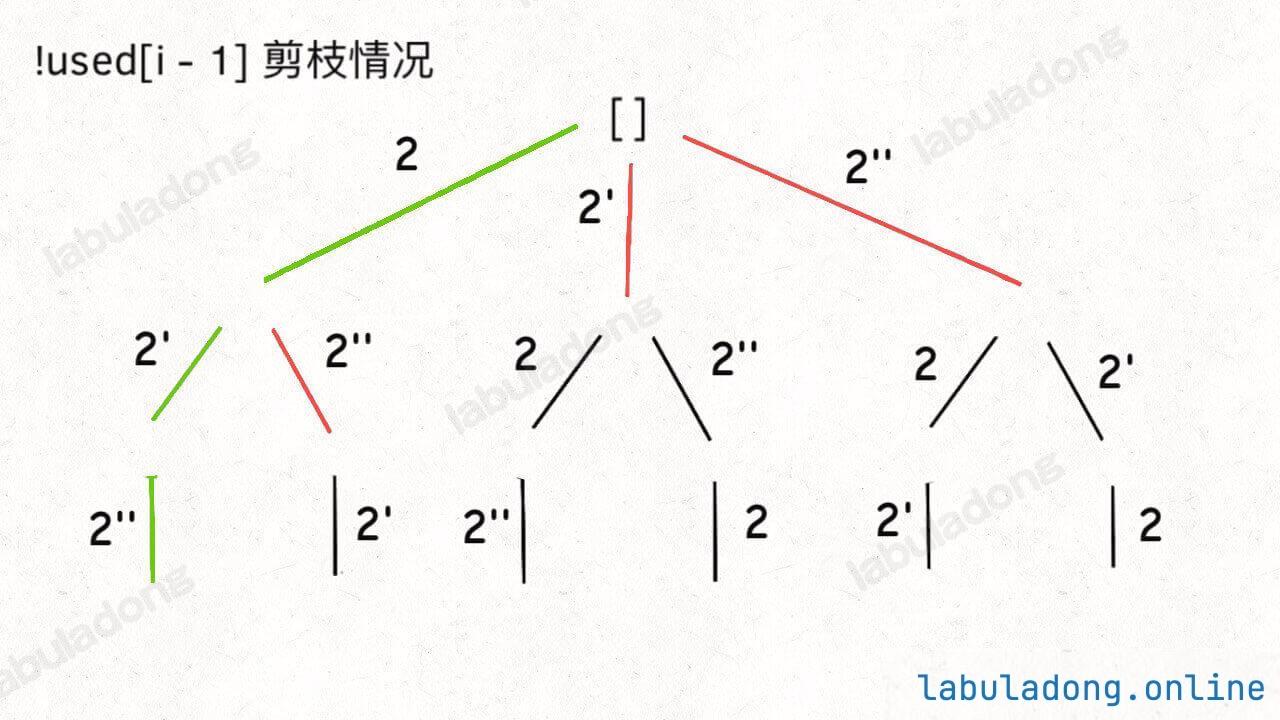
而 used[i - 1] 这种剪枝逻辑得到的回溯树如下：

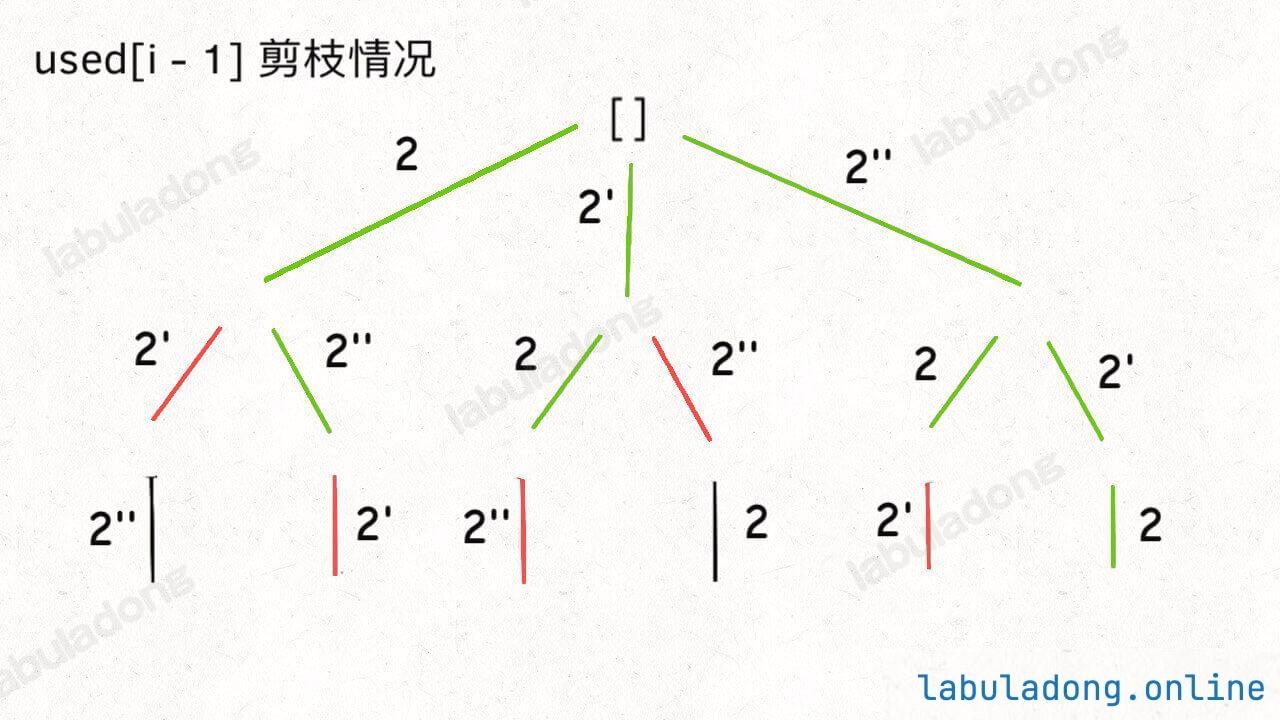
可以看到，!used[i - 1] 这种剪枝逻辑剪得干净利落，而 used[i - 1] 这种剪枝逻辑虽然也能得到无重结果，但它剪掉的树枝较少，存在的无效计算较多，所以效率会差一些。

3、元素无重可复选

3.1 子集/组合问题

终于到了最后一种类型了：输入数组无重复元素，但每个元素可以被无限次使用。

39. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40

这道题说是组合问题，实际上也是子集问题：candidates 的哪些子集的和为 target？

想解决这种类型的问题，也得回到回溯树上，我们不妨先思考思考，标准的子集/组合问题是如何保证不重复使用元素的？

答案在于 backtrack 递归时输入的参数 start：

这相当于给之前的回溯树添加了一条树枝，在遍历这棵树的过程中，一个元素可以被无限次使用：

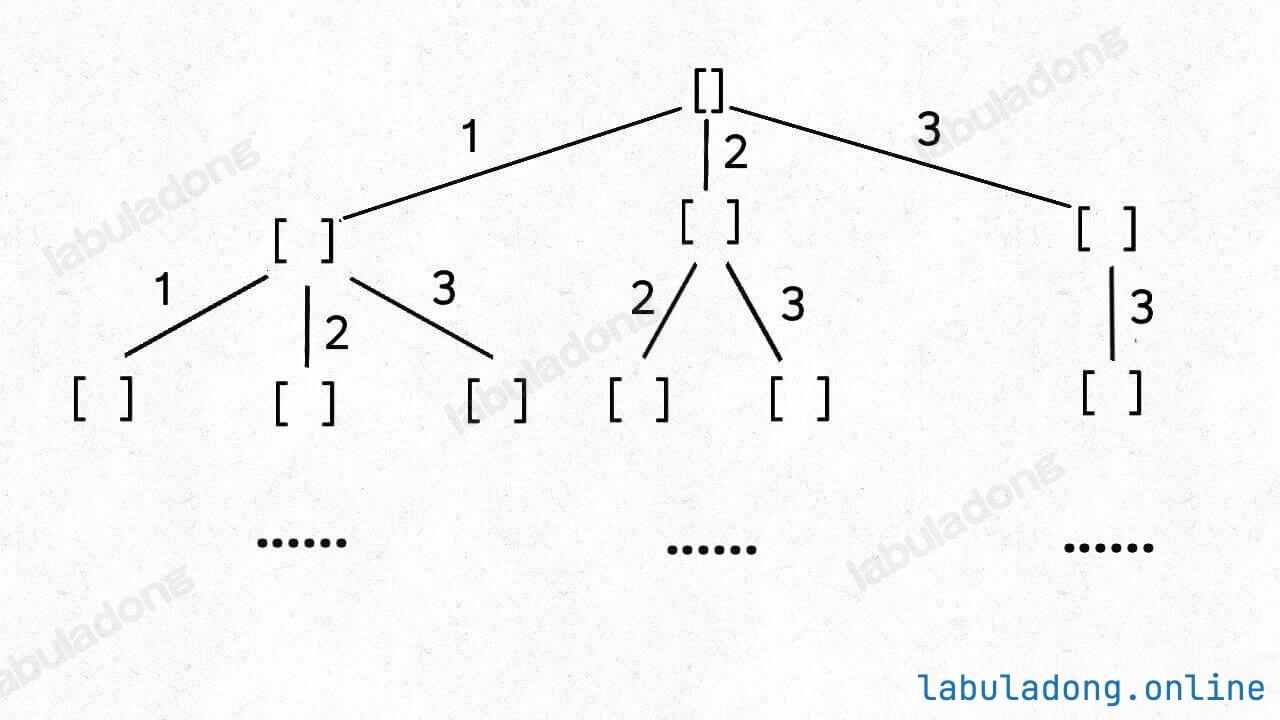
当然，这样这棵回溯树会永远生长下去，所以我们的递归函数需要设置合适的 base case 以结束算法，即路径和大于 target 时就没必要再遍历下去了。

# 无重组合的回溯算法框架
def backtrack(nums: List[int], start: int) -> None:
    for i in range(start, len(nums)):
        # ...
        # 递归遍历下一层回溯树，注意参数
        backtrack(nums, i + 1)
        # ...

这个 i 从 start 开始，那么下一层回溯树就是从 start + 1 开始，从而保证 nums[start] 这个元素不会被重复使用：

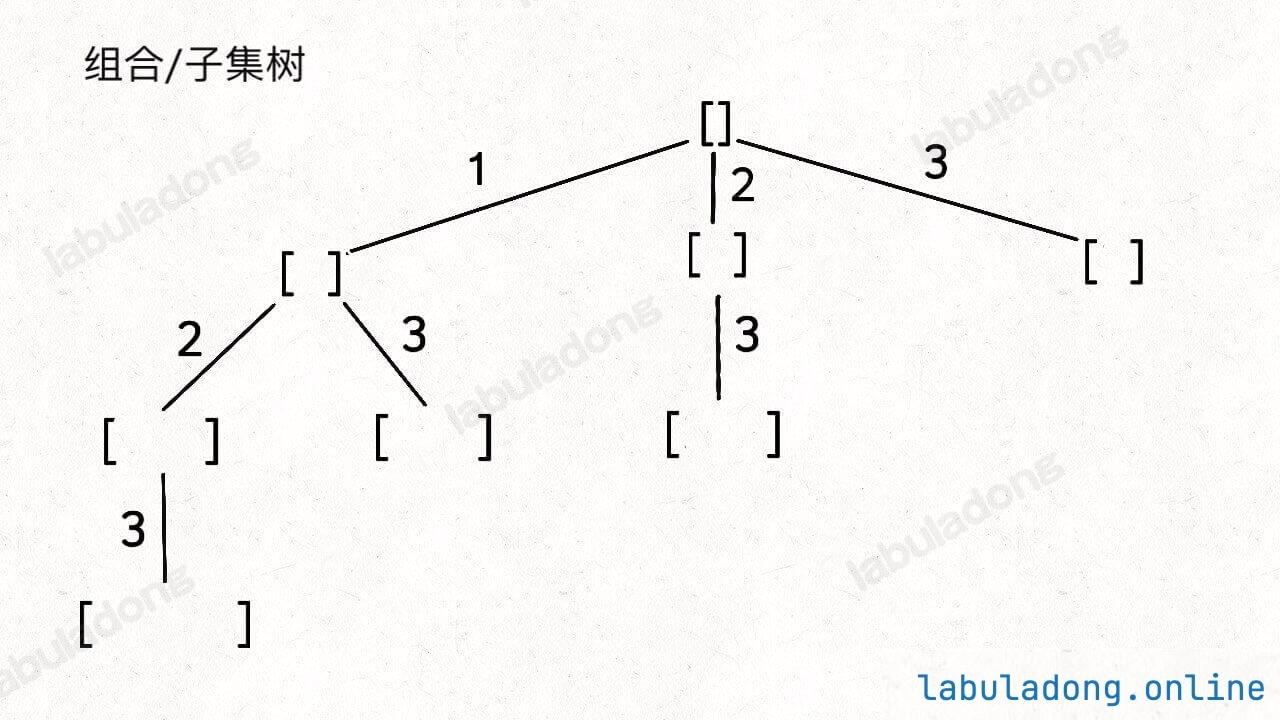
那么反过来，如果我想让每个元素被重复使用，我只要把 i + 1 改成 i 即可：

# 可重组合的回溯算法框架
def backtrack(nums: List[int], start: int):
    for i in range(start, len(nums)):
        # ...
        # 递归遍历下一层回溯树，注意参数
        backtrack(nums, i)
        # ...

这相当于给之前的回溯树添加了一条树枝，在遍历这棵树的过程中，一个元素可以被无限次使用：

当然，这样这棵回溯树会永远生长下去，所以我们的递归函数需要设置合适的 base case 以结束算法，即路径和大于 target 时就没必要再遍历下去了。

代码：

class Solution:
    def __init__(self):
        self.res = []
        # 记录回溯的路径
        self.track = []
        # 记录 track 中的路径和
        self.trackSum = 0

    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        if len(candidates) == 0:
            return self.res
        self.backtrack(candidates, 0, target)
        return self.res

    # 回溯算法主函数
    def backtrack(self, nums: List[int], start: int, target: int) -> None:
        # base case，找到目标和，记录结果
        if self.trackSum == target:
            self.res.append(list(self.track))
            return
        # base case，超过目标和，停止向下遍历
        if self.trackSum > target:
            return

        # 回溯算法标准框架
        for i in range(start, len(nums)):
            # 选择 nums[i]
            self.trackSum += nums[i]
            self.track.append(nums[i])
            # 递归遍历下一层回溯树
            # 同一元素可重复使用，注意参数
            self.backtrack(nums, i, target)
            # 撤销选择 nums[i]
            self.trackSum -= nums[i]
            self.track.pop()

3.2 排列

力扣上没有题目直接考察这个场景，我们不妨先想一下，nums 数组中的元素无重复且可复选的情况下，会有哪些排列？

比如输入 nums = [1,2,3]，那么这种条件下的全排列共有 3^3 = 27 种：

[
  [1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],
  [2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],
  [3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]
]

标准的全排列算法利用 used 数组进行剪枝，避免重复使用同一个元素。如果允许重复使用元素的话，直接放飞自我，去除所有 used 数组的剪枝逻辑就行了。

那这个问题就简单了，代码如下：

class Solution:
    
    def __init__(self):
        self.res = []
        self.track = []
    
    def permuteRepeat(self, nums: List[int]) -> List[List[int]]:
        self.backtrack(nums)
        return self.res

    # 回溯算法核心函数
    def backtrack(self, nums: List[int]) -> None:
        # base case，到达叶子节点
        if len(self.track) == len(nums):
            # 收集叶子节点上的值
            self.res.append(self.track[:])
            return

        # 回溯算法标准框架
        for i in range(len(nums)):
            # 做选择
            self.track.append(nums[i])
            # 进入下一层回溯树
            self.backtrack(nums)
            # 取消选择
            self.track.pop()

至此，排列/组合/子集问题的九种变化就都讲完了。

最后总结

来回顾一下排列/组合/子集问题的三种形式在代码上的区别。

由于子集问题和组合问题本质上是一样的，无非就是 base case 有一些区别，所以把这两个问题放在一起看。

形式一、元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，backtrack 核心代码如下：

# 组合/子集问题回溯算法框架
def backtrack(nums: List[int], start: int):
    # 回溯算法标准框架
    for i in range(start, len(nums)):
        # 做选择
        track.append(nums[i])
        # 注意参数
        backtrack(nums, i + 1)
        # 撤销选择
        track.pop()

# 排列问题回溯算法框架
def backtrack(nums: List[int]):
    for i in range(len(nums)):
        # 剪枝逻辑
        if used[i]:
            continue
        # 做选择
        used[i] = True
        track.append(nums[i])

        backtrack(nums)
        # 撤销选择
        track.pop()
        used[i] = False

形式二、元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次，其关键在于排序和剪枝，backtrack 核心代码如下：

nums.sort()
# 组合/子集问题回溯算法框架
def backtrack(nums: List[int], start: int):
    # 回溯算法标准框架
    for i in range(start, len(nums)):
        # 剪枝逻辑，跳过值相同的相邻树枝
        if i > start and nums[i] == nums[i - 1]:
            continue
        # 做选择
        track.append(nums[i])
        # 注意参数
        backtrack(nums, i + 1)
        # 撤销选择
        track.pop()


nums.sort()
# 排列问题回溯算法框架
def backtrack(nums: List[int]):
    for i in range(len(nums)):
        # 剪枝逻辑
        if used[i]:
            continue
        # 剪枝逻辑，固定相同的元素在排列中的相对位置
        if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:
            continue
        # 做选择
        used[i] = True
        track.append(nums[i])

        backtrack(nums)
        # 撤销选择
        track.pop()
        used[i] = False

形式三、元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次，只要删掉去重逻辑即可，backtrack 核心代码如下：

# 组合/子集问题回溯算法框架
def backtrack(nums: List[int], start: int):
    # 回溯算法标准框架
    for i in range(start, len(nums)):
        # 做选择
        track.append(nums[i])
        # 注意参数
        backtrack(nums, i)
        # 撤销选择
        track.pop()


# 排列问题回溯算法框架
def backtrack(nums: List[int]):
    for i in range(len(nums)):
        # 做选择
        track.append(nums[i])
        backtrack(nums)
        # 撤销选择
        track.pop()

只要从树的角度思考，这些问题看似复杂多变，实则改改 base case 就能解决，这也是为什么我在学习算法和数据结构的框架思维和手把手刷二叉树（纲领篇）中强调树类型题目重要性的原因。

风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。