您现在的位置是：首页 >技术教程 >CF 868 div2 A—C网站首页技术教程

A 题就是一个预处理然后进行枚举

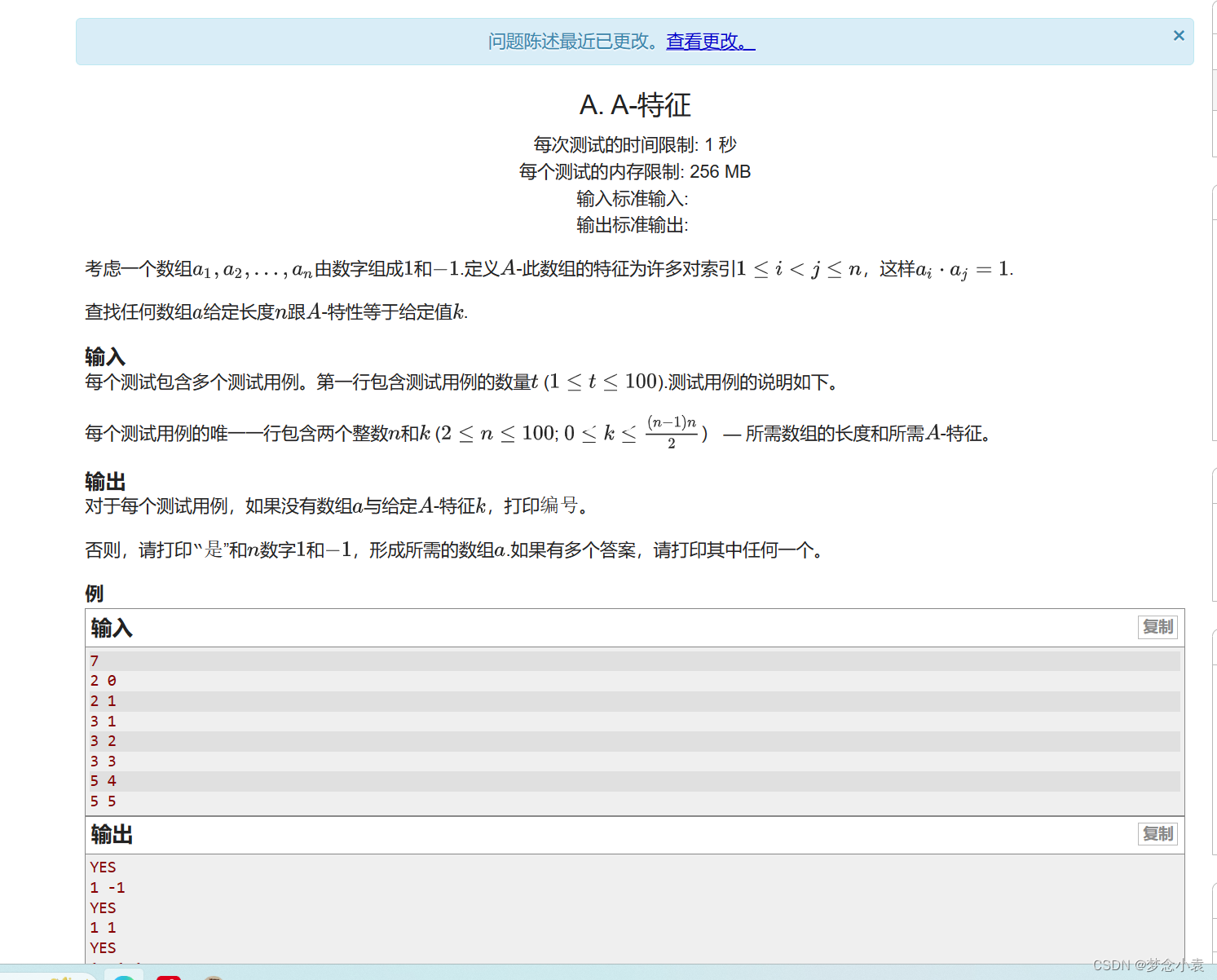
首先数据范围不是很大

 然后我们依照题意看看如何构造出对应的要求，也就是说我们需要在不同的下标下使得 ai*aj=1 那么只有1 1 或者-1 -1 那么这个不管是1 1 还是-1 -1  必然是对称的    那么要多少个1 可以组成对应要求 我们可以发现（简单数学）

如果是一个1 那么就是0 

两个1  就是1

3 个1 就是 2

也就是从 2 之后每次出现的1 都可以和前面的所有的1 组合

那么对应每个1 的个数我们就可以预处理出可以组成多少不同下标乘积是1 （ai*aj==1）

那么对于 -1 是同理

void intn()
{
    f[2]=1;
    for(int i=3;i<=111;i++) f[i]=f[i-1]+i-1;
}

那么由于我们可以使用1 的组合以及-1 的组合那么所有的组合的答案就是

1 的答案加上-1 的答案

for(int i=1;i<=n;i++)
    {
        if(f[i]+f[n-i]==m)
        {
            cout<<"YES"<<endl;
            for(int j=1;j<=i;j++) cout<<1<<" ";
            for(int j=1;j<=n-i;j++) cout<<-1<<" ";
            cout<<endl;
            return ;
        }
    }

AC 代码如下捏 

// 数学公式要变形
// 莫急莫急先读题
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&(-x))
#define endl "
"
#define ios ios::sync_with_stdio(0); cin.tie(0),cout.tie(0);
#define LF(x)   fixed<<setprecision(x)// c++ 保留小数
typedef long long LL;
typedef pair<int,int> PII;
const int N=1000010,M=1010,F=2*N,INF=0x3f3f3f3f;
const double pai=acos(-1.0);// pai
map<int,int> q;
int t,n,m;
int f[N],ans[N];
void intn()
{
    f[2]=1;
    for(int i=3;i<=111;i++) f[i]=f[i-1]+i-1;
}
void solve()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        if(f[i]+f[n-i]==m)
        {
            cout<<"YES"<<endl;
            for(int j=1;j<=i;j++) cout<<1<<" ";
            for(int j=1;j<=n-i;j++) cout<<-1<<" ";
            cout<<endl;
            return ;
        }
    }
    cout<<"NO"<<endl;
        return ;
}

int main ()
{
    ios// 不能有printf puts scanf
    intn();
    cin>>t;
    while(t--)
    solve();
    return 0;
}

B题就是一个类似模拟的位置变化要找到核心

1.首先我们要搞清楚一个元素会被如何交换一个元素只能被交换到 现在的位置和m差值的倍数的位置那么如果一个数没办法通过m的交换到达自己的位置那必然药进行初步交换，到这里答案就出来的

比如   一个数的下标是1 m=3 那么1 只会移动到 4  7 10.....

2.有人说为什么会这样想 其实你要发掘题目给的性质 要深入去思考 然后自己模拟一下 这个有些题就很快能思考到

3。那么如果错位的也就是没办法通过m交换达到的如果要初次交换 那么一定是两个  （有人会问会不会是一个呢？） 你可以试试或者再思考一下是不会的

那么多余2的就是不可以通过初次交换的咯 

// 数学公式要变形
// 莫急莫急先读题
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&(-x))
#define endl "
"
#define ios ios::sync_with_stdio(0); cin.tie(0),cout.tie(0);
#define LF(x)   fixed<<setprecision(x)// c++ 保留小数
typedef long long LL;
typedef pair<int,int> PII;
const int N=1000010,M=1010,F=2*N,INF=0x3f3f3f3f;
const double pai=acos(-1.0);// pai
map<int,int> q;
int t,n,m;
int a[N];
void solve()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(abs(a[i]-i)%m!=0) ans++; 
    }
    if(!ans) cout<<0<<endl;
    else if(ans==2) cout<<1<<endl;
    else cout<<-1<<endl;
        return ;
}

int main ()
{
    ios// 不能有printf puts scanf
    cin>>t;
    while(t--)
    solve();
    return 0;
}

C题是一个模拟？思考思考其实不难

1. 首先要知道啥是强复合 然后思考如何组成强复合

2. 题目意思是要通过a1*a2*a3*....*ai 而且a的范围是2-1e7 那么连乘会爆 这是一种算是提醒必然是对每一个数单独处理    题目要求构造强复合数去和a的连乘相等要让b数组的长度最大

3. 那么我们就要利用a的元素去构造b那么由于和质数有关那么我们就想是不是要把a分解质数？

还有何如构造使得b最长呢？ b最长那就是使得每个b的元素越小并且满足要求越好 也就是如何构造最小的强复合数   所有的答案都指向了质数 那么我们就开始看 如何变 我们可以发现如果是一个质数和他自己配对的话直接就是强复合

（1）比如 2    2*2=4  4是强复合

也就是如果a是质数  那么b=a*a    b 的约数是1 a b 那么b就是强复合  所以对于每一个质数和自己的乘积都是强复合

（2）如果不是自己呢？ 我们可以试一下  2  3 乘积是6 那么6 的约数是  1 2 3 6 不是

但是如果是3 个不同的呢  2 3 5     30  的约数是1 2 3 5 6 1015 30 是强复合为啥呢？因为每两个不同质数可以构造一个合数  那么3 个不同的就可以构造  3 个加上3个数连乘 就是4 个了那么此时也可以    对于以上我们就 不用考虑了

那么如何把ai同质数连续起来呢？ 我的上一篇博客也提到了就是质数分解定理时间复杂度根号n

int x; cin>>x;
        for(int i=2;i*i<=x;i++)
        {
            if(x%i==0)
            {
                while(x%i==0) x/=i,q[i]++;
            }
        }
        if(x>1) q[x]++;

 为要判断x>1 呢？ 因为可能是一个大质数

如果有小伙伴有疑惑于质数分解定理可以自己用线性筛的思维去思考一下就会理解了

然后你当然要把每一个数的算在一起可不能每个数单独用一个数组存起来 这样就会少算

把2 的加起来  3 的加起来   依次类推（map大法）

for(auto &[k,v]:q) 
    {
        ans+=v/2;
        m+=v%2;
    }
    ans+=m/3;

然后取出来每一个数的数量然后把多的加起来最后除以3 就好了

当然写之前要自己看一下时间复杂度 当然是稳的再开始写不然就自己再思考优化一下不然被tle哦

// 数学公式要变形
// 莫急莫急先读题
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&(-x))
#define endl "
"
#define ios ios::sync_with_stdio(0); cin.tie(0),cout.tie(0);
#define LF(x)   fixed<<setprecision(x)// c++ 保留小数
typedef long long LL;
typedef pair<int,int> PII;
const int N=10000010,M=1010,F=2*N,INF=0x3f3f3f3f;
const double pai=acos(-1.0);// pai
map<LL,int> q;
int t,n;
void solve()
{
    cin>>n;
    LL cnt=0,ans=0,m=0;
    for(int i=1;i<=n;i++) 
    {
        int x; cin>>x;
        for(int j=2;j*j<=x;j++)
        {
            if(x%j==0)
            {
                while(x%j==0) x/=j,q[j]++;
            }
        }
        if(x>1) q[x]++;
    }
    for(auto &[k,v]:q) 
    {
        ans+=v/2;
        m+=v%2;
    }
    ans+=m/3;
    cout<<ans<<endl;
    q.clear();
        return ;
}

int main ()
{
    ios// 不能有printf puts scanf
    cin>>t;
    while(t--)
    solve();
    return 0;
}

后面的题由于本人实力不够就没啦，一起进步吧，如有问题欢迎读者指正，觉得还行就给一个免费的赞支持一下吧嘻嘻🤭