【LeetCode】HOT 100（11）网站首页 技术交流

【LeetCode】HOT 100（11）

戊子仲秋 2024-10-26 12:01:04

简介【LeetCode】HOT 100（11）

题单介绍：

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。

题单介绍：

题目：64. 最小路径和 - 力扣（Leetcode）

题目：72. 编辑距离 - 力扣（Leetcode）

题目：64. 最小路径和 - 力扣（Leetcode）

题目的接口：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {

    }
};

解题思路：

这道题也是简单dp，

主要思路就是：（三种情况）

1. 第一行的值就是自己的值加上左边数的值

2. 第一列的值就是自己的值加上上面数的值

3. 其它位置就是自己的值加上min(左边数的值，上面数的值)（因为是找最小值路径）

代码：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        for(int i = 0; i < grid.size(); i++) {
            for(int j = 0; j < grid[0].size(); j++) {
                if(i == 0 && j == 0) continue; //第一行第一列就是自己本身
                else if(i == 0) grid[i][j] = grid[i][j - 1] + grid[i][j]; //情况1
                else if(j == 0) grid[i][j] = grid[i - 1][j] + grid[i][j]; //情况2
                else grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j]; //情况3
            }
        }
        return grid[grid.size() - 1][grid[0].size() - 1];
    }
};

过过过过啦！！！！

题目：72. 编辑距离 - 力扣（Leetcode）

题目的接口：

class Solution {
public:
    int minDistance(string word1, string word2) {

    }
};

解题思路：

这道题也是dp问题，算是不怎么基础的基础dp问题吧，

这道题的状态转移方程我也是看了很久才看明白，

具体思路是这样子的：

1. 我们将操作一个单词分成三种情况：插入、删除、替换

2. 初始化用于动态规划的二维数组，将第一行作为插入操作，第一列作为删除操作初始化其操作数

3. 三种操作分别对应上，左，左上。（左上对应的是替换操作）

然后我们列出状态转移方程：（因为要求的是最小的步数）

1. 如果单词需要操作，找出三种操作中最小一步 + 1次操作

2. 如果单词不需要操作，就不操作（返回之前的样子）

代码如下：

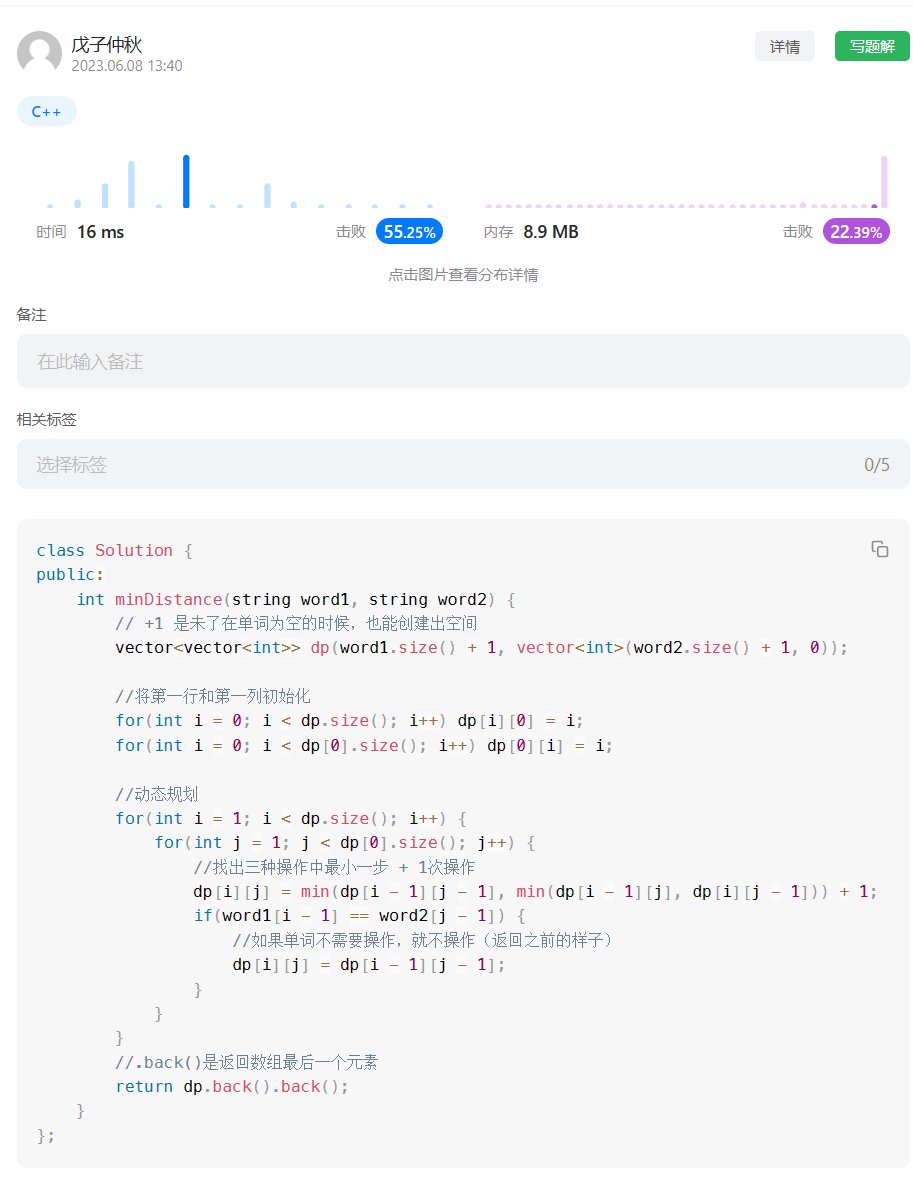
代码：

class Solution {
public:
    int minDistance(string word1, string word2) {
        // +1 是未了在单词为空的时候，也能创建出空间
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));

        //将第一行和第一列初始化
        for(int i = 0; i < dp.size(); i++) dp[i][0] = i;
        for(int i = 0; i < dp[0].size(); i++) dp[0][i] = i;

        //动态规划
        for(int i = 1; i < dp.size(); i++) {
            for(int j = 1; j < dp[0].size(); j++) {
                //找出三种操作中最小一步 + 1次操作
                dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
                if(word1[i - 1] == word2[j - 1]) {
                    //如果单词不需要操作，就不操作（返回之前的样子）
                    dp[i][j] = dp[i - 1][j - 1];
                }
            }
        }
        //.back()是返回数组最后一个元素
        return dp.back().back();
    }
};