栈的应用

递归的实现是栈：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。栈在计算机领域中应用是非常广泛的。像我们经常用的可视化软件例如APP、网站之类的，其底层很多功能的实现都是基础的数据结构和算法。

一、栈在系统中的应用

根据编译原理，编译器在词法分析的过程中处理括号、花括号等这个符号的逻辑，就是使用了栈这种数据结构。

简化路径(leetcode. 71)

class Solution:
    def simplifyPath(self, path: str) -> str:
        #对于路径中出现两个点或者目录名，我们则可以用一个栈来维护路径中的每一个目录名
        #当我们遇到两个点时，需要将目录切换到上一级，因此只要栈不为空，我们就弹出栈顶的目录
        #当我们遇到目录名，就把它放入栈
        #这样一来，我们只需要遍历names中的每个字符串并进行上述操作即可。
        #在所有的操作完成后，我们将从栈底到栈顶的字符串用/进行连接，再在最前面加上/表示根目录，就可以得到简化后的规范路径
        names=path.split("/")#通过分隔符对字符串路径切片，并返回分割后的字符串列表（list）
        stack=list()#创建一个空列表
        for name in names:
            if name == "..":
                if stack:
                    stack.pop()
            elif name and name!=".":
                stack.append(name)
        return "/"+"/".join(stack)#以分隔符/开头，并且列表stack元素之间以字符/连接

复杂度分析:时间复杂度O(n) ，其中n是字符串path的长度；空间复杂度O(n)我们需要O(n)的空间存储names中的所有字符串。

二、扩号匹配问题

思路：在写代码之前，我们需要先分析问题，有哪几种不匹配情况，如果不分析清楚，写出来的代码容易出问题！
大概有三种不匹配的情况：

1. 字符串里左方向的括号多余了，所以不匹配。
   左括号多余了，是说右边没有出现与之匹配的右括号直接只出现左括号。这里只是做了个简单的举例供大家参考。
   

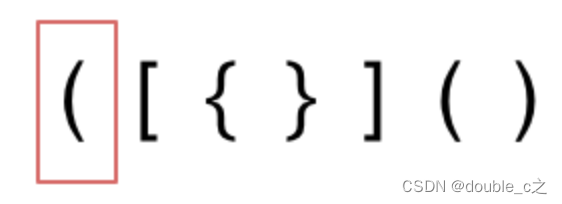
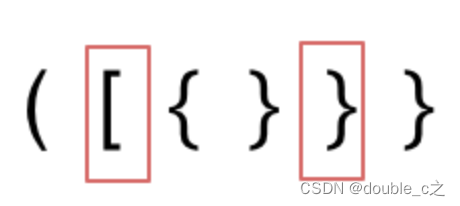
2. 括号没有多余，但是括号的类型没有匹配上。
   

3. 字符串里右方向的括号多余了，所以不匹配。
   右括号多余了，是说左边没有出现与之匹配的左括号直接只出现右括号。这里只是做了个简单的举例供大家参考。
   

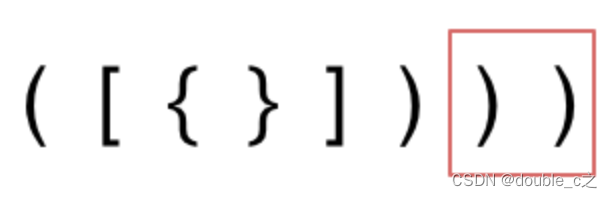
注意：在匹配左括号的时候，右括号先入栈，就只需比较当前元素和栈顶相不相等就可以了，比左括号先入栈代码实现要简单许多！具体来说就是，当遇到左括号时，我们是把对应的右括号入栈，而不是直接把左括号入栈，不断遍历，直到我们遍历到右方向元素遇到一个右括号，判断当前右括号元素是否与栈顶元素相等，相等就把该栈顶元素pop出去。如果我们字符串遍历完了，但是栈不为空，此时说明不匹配，左括号多了。 或者字符串还没遍历完，栈就为空了，此时说明不匹配，右括号多了。或者字符串没遍历完，元素与栈顶元素不匹配，此时说明括号类型不匹配。
类似于C++的伪代码：

stack<char> st;
if (s.size()%2!=0)
	return false;
#遍历字符串
for (i=0;i<s.size();i++){
#先处理左括号的场景
	if (s[i]=='(')
		st.push(')');
	elseif(s[i]=='{')
		st.push('}');
	elseif(s[i]=='[')
		st.push(']');
#再来处理右括号的场景
	elseif(st.empty() || st.top()!=s[i]):#第二种、三种不匹配情况处理了
		return false;
	else:
		st.pop();		
}
return st.empty();#处理第一种不匹配情况
	

有效的括号(leetcode. 20)

代码如下（示例）：

# 仅使用栈，更省空间
class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        for item in s:
            if item == '(':
                stack.append(')')
            elif item == '[':
                stack.append(']')
            elif item == '{':
                stack.append('}')
            elif not stack or stack[-1] != item:
                return False
            else:
                stack.pop()
        
        return True if not stack else False

还可使用字典去做这道题

class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        mapping = {
            '(': ')',
            '[': ']',
            '{': '}'
        }
        for item in s:
            if item in mapping.keys():
                stack.append(mapping[item])
            elif not stack or stack[-1] != item: 
                return False
            else: 
                stack.pop()
        return True if not stack else False

三、字符串去重

思路：用栈来存我们遍历过的元素，当遍历到的元素与栈顶元素相同则pop栈顶元素，消除重复项，否则就压入栈，继续遍历，最后我们从栈中弹出剩余元素，因为从栈里弹出的元素是倒序的，所以再对字符串进行反转一下，就得到了最终的结果。
没有必要真的用一个栈去做，可以用字符串去模拟这个栈的行为。用栈顶作为字符串的尾部，栈的另一端作为字符串的头部。

伪代码

string result;
for(char s:S){
	if (result.empty()||s!=result.back())
		result.push_back(s);
	else:
		result.pop_back();
}
	return result;#返回字符串自然就是正确的答案，不用再反转。

时间复杂度: O(n)
空间复杂度: O(1)，返回值不计空间复杂度

删除字符串中的所有相邻重复项(leetcode. 1047)

代码如下（示例）：

class Solution:
    def removeDuplicates(self, s: str) -> str:
        res = list()
        for item in s:
            if res and res[-1] == item:
                res.pop()
            else:
                res.append(item)
        return "".join(res)  # 字符串拼接

时间复杂度: O(n)
空间复杂度: O(n)

四、逆波兰表达式问题

思路：逆波兰表达式就是后缀表达式RPN，比如中缀表达式(1+2)x(3+4)，表示成二叉树的后续遍历。后缀表达式为(12+34+x). 遍历元素1、2入栈，再遍历+号，弹出元素1、2进行+运算，并把运算结果放入栈内，继续遍历元素加入栈，重复上述过程！整个表达式的结果就是栈里最后一个元素。


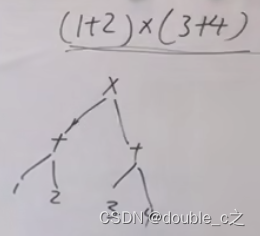
所以后缀表达式对计算机来说是非常友好的。本题也展现出计算机的思考方式，计算机可以利用栈来顺序处理，不需要考虑优先级了，也不用回退了。在1970年代和1980年代，惠普在其所有台式和手持式计算器中都使用了RPN（后缀表达式），直到2020年代仍在某些模型中使用了RPN。(参考自维基百科)

逆波兰表达式求值(leetcode. 150)

代码如下

from operator import add, sub, mul

class Solution:
    op_map = {'+': add, '-': sub, '*': mul, '/': lambda x, y: int(x / y)}
    
    def evalRPN(self, tokens: List[str]) -> int:
        stack = []
        for token in tokens:
            if token not in {'+', '-', '*', '/'}:
                stack.append(int(token))
            else:
                op2 = stack.pop()
                op1 = stack.pop()
                stack.append(self.op_map[token](op1, op2))  # 第一个出来的在运算符后面
        return stack.pop()
        

时间复杂度: O(n)
空间复杂度: O(n)

总结

本文介绍了栈在计算机领域的应用。让我们看到了不一样的栈，原来还有这么多的应用，不可小觑！数据结构与算法的应用往往隐藏在我们看不到的地方！
(ps:近期都是关于数据结构基础知识分享，感兴趣的同学可以关注本人公众号：HEllO算法笔记）