您现在的位置是:首页 >技术教程 >【OTFS与信号处理:论文阅读】:考虑分数多普勒的OTFS系统有效信道估计网站首页技术教程
【OTFS与信号处理:论文阅读】:考虑分数多普勒的OTFS系统有效信道估计
2023.06.05 最近在研究OTFS考虑分数多普勒时信道估计与信号检测相关问题,最近精读了一篇论文,并针对论文中部分公式进行推导,故记录一下学习过程。
【OTFS与信号处理:论文阅读】Efficient Channel Estimation for OTFS Systems in the Presence of Fractional Doppler
前言
论文题目: Efficient Channel Estimation for OTFS Systems in the Presence of Fractional Doppler
论文地址: https://ieeexplore.ieee.org/document/10118609/
论文来源:2023 IEEE Wireless Communications and Networking Conference (WCNC)
论文主要研究了OTFS考虑分数多普勒的信道估计问题,分别考虑单径和多径两种情况,引入线性系统去恢复不同可分解路径的多普勒频移以及信道增益。
一、摘要及背景
摘要
论文提出了一个考虑分数多普勒的有效的信道估计算法。该算法首先设置了一个基于现有阈值的估计器以获得有效的(初步)信道响应。由于有效的信道矩阵已知(可能翻译的不准确),然后使用线性系统去恢复不同可分解路径的多普勒频移以及信道增益。在这一过程中,考虑了不同路径间的干扰。仿真表明,通过在有效信道矩阵中选择最优采样值,可以在低信噪比条件下实现多普勒频移和信道增益的鲁棒估计。
分数多普勒的引入
准确的信道估计对于获取用于可靠检测的信道状态信息 (CSI) 至关重要。 在OTFS中,信道信息即时延偏移和多普勒偏移在 DD 网格上是离散的。 时延分辨率和多普勒分辨率分别取决于带宽和持续时间。 实际通信场景中,带宽足够大以提供足够的时延分辨率,而由于未来通信中的低时延要求,持续时间可能相对较小。(此时解释了为什么不会特别考虑分数时延的问题) 因此,需要考虑分数多普勒。 在整数多普勒的情况下,DD域的有效通道是稀疏的。 相反,对于分数多普勒情况,有效DD主信道分布在所有多普勒指数上,这牺牲了有效信道的稀疏性,因此可能会降低信道估计性能 。 针对这一挑战,为分数多普勒情况开发一种有效的信道估计算法至关重要。
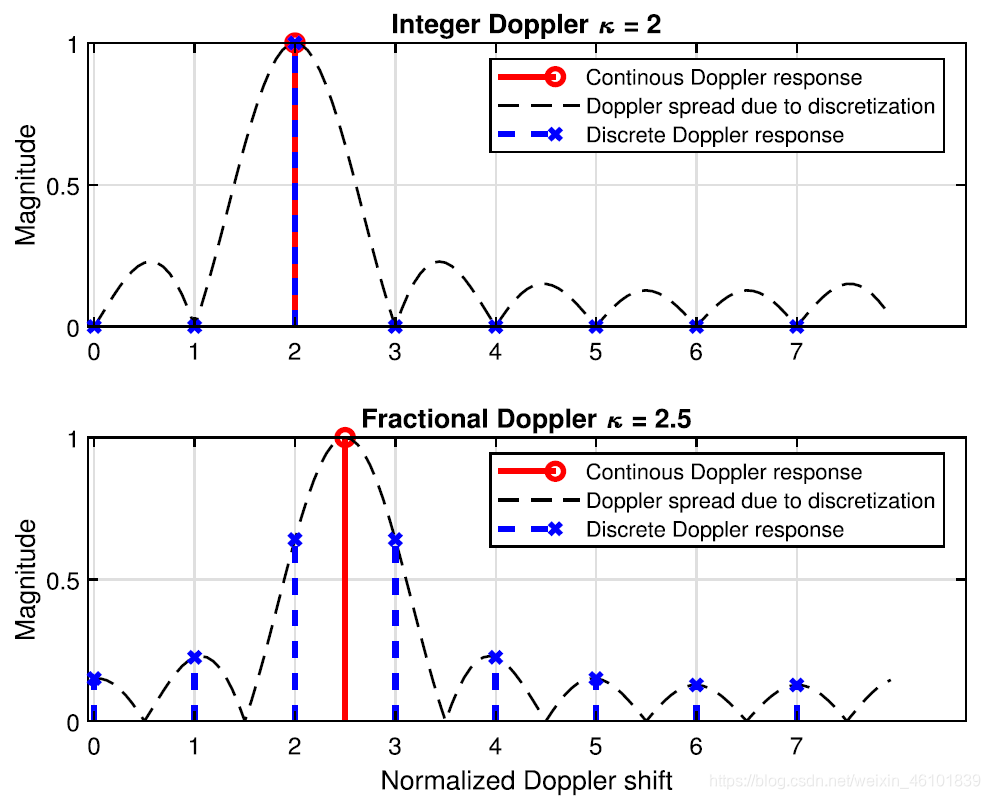
估计分数多普勒的意义
i)使我们能够通过使用估计的多普勒频移,重建有效的DD域信道来改进信道估计,这对于可靠检测是必不可少。
ii)提高了定位的精度:当OTFS辅助传感时,因为可以通过多普勒频移的准确估计来获得移动用户速度的准确估计。
研究现状
目前已有许多信道估计方面的论文([5]-[10])针对分数多普勒场景下做出研究。论文[5]提出了一种嵌入式导频设计,并引入一个简单的基于门槛的估计器用来恢复DD域有效信道,该论文的缺点在于该方法并未提供多普勒频移和信道增益方面的估计(具体细节需要参考论文[5])。论文[6]提出一个三维正交匹配追踪算法结构,以实现三维稀疏性结构在时延-多普勒-角度域信道的有效估计。论文[7]提出了一个改进的导频图案,在导频和符号间不再需要保护间隔,此外引入系数贝叶斯(后文简称为SBL)算法解决稀疏信号恢复的问题。论文[11]通过引入块重组,提出块SBL算法。实现该论文的基础上进行改进。论文[7][11]由于使用SBL算法复杂度较高,特别不适用于OTFS帧较大的场景。论文[12]研究了多导频方案也将信道估计问题建模为稀疏信号恢复问题进行求解,引入基于因子图表示的消息传递算法直接实现信道增益以及多普勒频移的估计。论文[9]提出无格点的信道估计方案实现原始DD域的估计而非有效DD域估计(此处不太理解原始和有效DD域估计的区别是什么?为什么这里要特别强调?),该方法将信道估计问题建模为1D和2D无格点稀疏恢复问题(此处也不太理解从信道估计到稀疏信号恢复问题间的转换关系?),并引入SBL算法来解决以上问题(1D和2D无格点稀疏恢复问题)。
本节参考文献
[5] P. Raviteja, K. T. Phan, and Y. Hong, “Embedded pilot-aided channel estimation for OTFS in delay-doppler channels,” IEEE Transactions on Vehicular Technology, vol. 68, no. 5, pp. 4906-4917, 2019.
[6] W. Shen, L. Dai, J. An, P. Fan, and R. W. Heath, “Channel estimation for orthogonal time frequency space (OTFS) massive MIMO,” IEEE Transactions on Signal Processing, vol. 67, no. 16, pp. 4204-4217, 2019.
[7] L. Zhao, W. Gao, and W. Guo, “Sparse bayesian learning of delay- doppler channel for OTFS system,” IEEE Communications Letters, vol. 24, no. 12, pp. 2766-2769, 2020.
[8] W. Yuan, S. Li, Z. Wei, J. Yuan, and D. W. K. Ng, “Data-aided channel estimation for OTFS systems with a superimposed pilot and data transmission scheme,” IEEE Wireless Communications Letters, vol. 10, no. 9, pp. 1954-1958, 2021.
[9] Z. Wei, W. Yuan, S. Li, J. Yuan, and D. W. K. Ng, “Off-grid channel estimation with sparse bayesian learning for OTFS systems,” IEEE Transactions on Wireless Communications, pp. 1-1, 2022.
[10] Z. Li, W. Yuan, and L. Zhou, “UAMP-based channel estimation for OTFS in the presence of the fractional doppler with HMM prior,” in 2022 IEEE/CIC International Conference on Communications in China (ICCC Workshops), 2022, 304-308.
[11] L. Zhao, J. Yang, Y. Liu, and W. Guo, “Block sparse bayesian learning- based channel estimation for mimo-OTFS systems,” IEEE Communica- tions Letters, vol. 26, no. 4, pp. 892-896, 2022.
[12] F. Liu, Z. Yuan, Q. Guo, Z. Wang, and P. Sun, “Message passing-based structured sparse signal recovery for estimation of OTFS channels with fractional doppler shifts,” IEEE Transactions on Wireless Communica- tions, vol. 20, no. 12, pp. 7773-7785, 2021.
二、系统模型
OTFS在DD域的输入输出关系可以表述为:
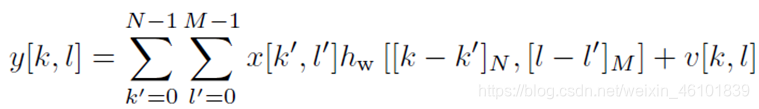
其中,x和y分别表示在DD域上的发送和接收符号,h_w表示有效DD域信道,其中,采样后信道的响应可以表示为:
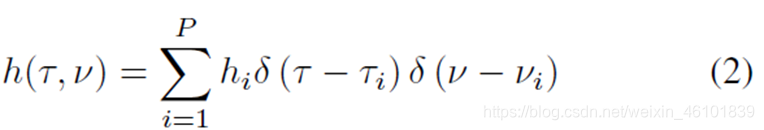
考虑分数多普勒后,时延和多普勒为τi和vi分别表示为:
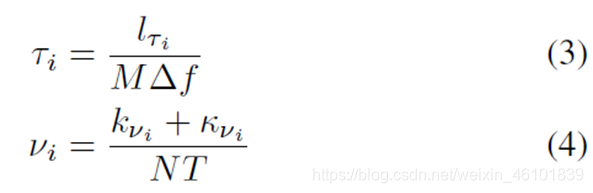
κ
kappa
κvi∈[-1/2,1/2]为分数多普勒。
因此,整数时延和分数多普勒信道可以表示为:
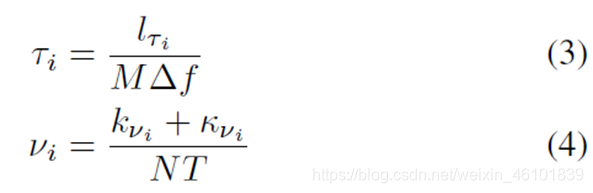
若只考虑一条路径,可以将上式简化为:
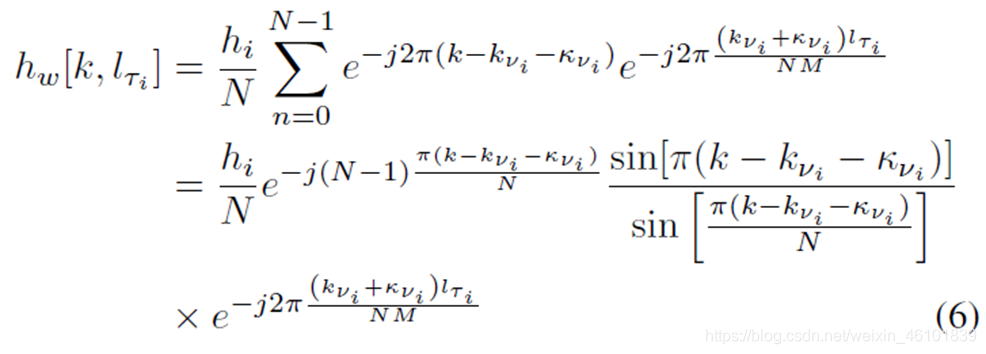
补充其推导过程(特别注意这里原文中的公式存在笔误):

简化为:
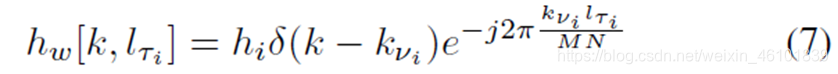
分数多普勒时(即
κ
kappa
κvi≠0),可以将DD域信道响应的幅度为:
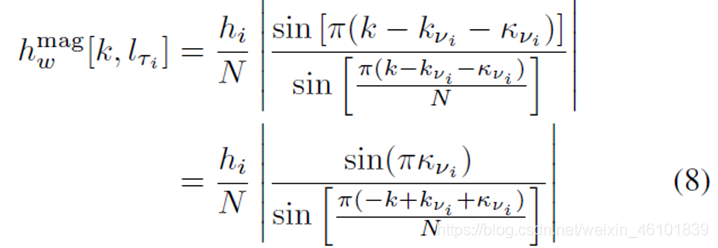
从上式可以看出,分数多普勒降低了信道估计的性能,增加了符号检测的复杂度。
三、论文算法
概述
提出一个用于OTFS系统的基于线性系统信道估计算法,该算法可以提取多普勒频移和信道增益,即使不同路径间存在明显的干扰;在低信噪比下,通过从有效信道向量中选择合适的样本,可以初步估计多普勒频移和信道增益。
导频设计
采用嵌入式导频设计,具体细节参考[1]。
算法细节
导频处实际接收到的符号包括三部分:导频处接收符号(该项通过阈值法实现初步接收,具体操作见[1])+分数多普勒产生的干扰+噪声。对于接收信号的进一步准确估计主要分为两种情况分析:
A .单径(路径间无干扰) B. 多径。
A. 单一路径下的精确估计(相当于给定时延)
由式6可知,给定时延的信道响应为:

由上式可知,通过信道响应gi(k)
α
alpha
αizi(得到这两项后,容易得到路径增益和多普勒频移),即
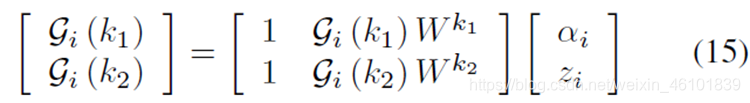
因此,路径增益和多普勒频移的精确估计就可以转化为求信道响应gi(k)的最优采样值;最优采样值的选取即找到能量最大的信道响应即可:
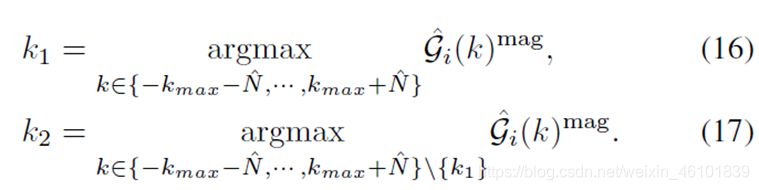
B. 多路径下的精确估计
当多普勒索引可以明显分离时,多径多普勒估计问题可以简化为单径问题处理,当多普勒索引彼此很近时,需要引入多径场景单独处理,因此将问题建模成:
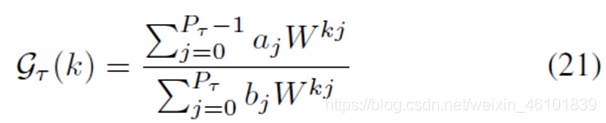
与单径场景类似:
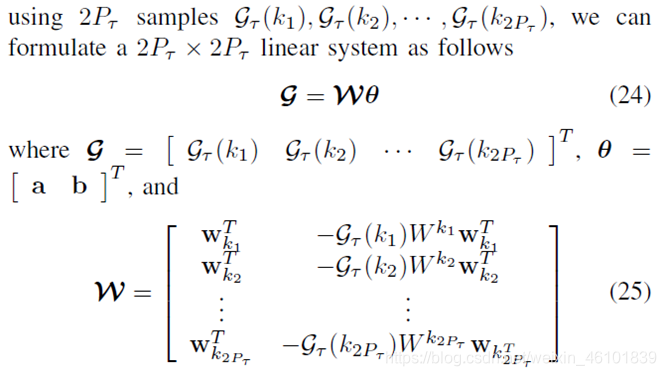
将该问题用线性系统进行表示,通过选择幅度最大的Pτ从而恢复出系数a和b,在这一基础上,通过下式恢复出多普勒频移和信道增益:

四、仿真结果
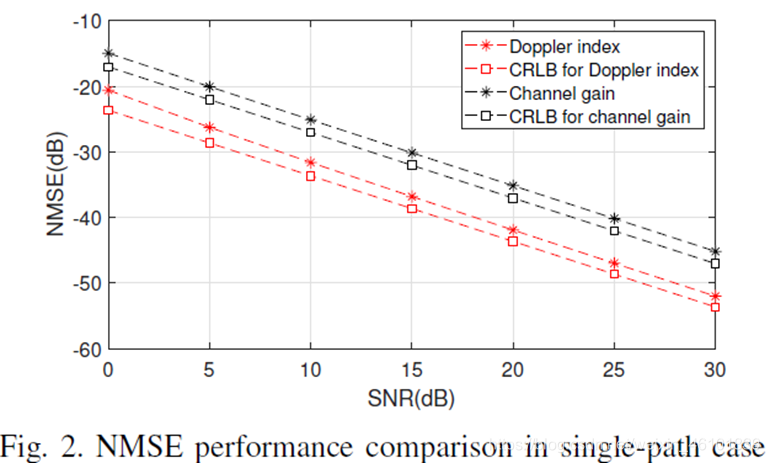
参数设置:OTFS帧尺寸M=N=32,子载波间隔为7.5kHz,载波频率为3GHz,路径数P=5,归一化最大时延和多普勒为5和4,QPSK调制。
A. 单径:
B. 多径:
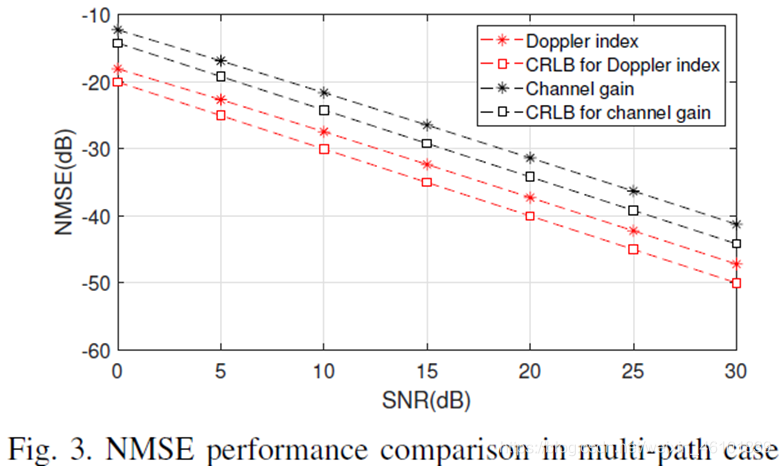
从上述仿真结果可以看出,无论是再单径还是多径场景下,该算法估计的信道增益与多普勒频移与CRLB很接近。由于不同路径间存在干扰,多径下的CRLB与单径相比NMSE更高(关于CRLB的推导过程见[3])。
五、总结
以上为对于该论文的整理与串联,关于与本人目前研究非强相关的内容未作详细推导,建议辅助原文阅读效果最佳。
参考文献
[1] P. Raviteja, K. T. Phan, and Y. Hong, “Embedded pilot-aided channel estimation for OTFS in delay–doppler channels,” IEEE Transactions on Vehicular Technology, vol. 68, no. 5, pp. 4906–4917, 2019.
[2] A. F. Molisch, “Delay-Doppler Communications: Principles and Applications,” in IEEE Communications Magazine, vol. 61, no. 3, pp. 10-10, March 2023, doi: 10.1109/MCOM.2023.10080900.https://ieeexplore.ieee.org/document/10080900
[3] F. Liu, Z. Yuan, Q. Guo, Z. Wang, and P. Sun, “Message passing-based structured sparse signal recovery for estimation of OTFS channels with fractional doppler shifts,” IEEE Transactions on Wireless Communications, vol. 20, no. 12, pp. 7773–7785, 2021.
[4] 知乎:OFDM同步技术(2)——小数倍载波频率偏差估计https://zhuanlan.zhihu.com/p/337633382
(本文并未引用,但是若想要学习分数多普勒问题建议看看。此外,可以将OTFS分数多普勒的问题转到OFDM中小数CFO中研究,这样资料和公式推导都会完善许多。)






 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结