?博主CSDN主页:杭电码农-NEO?
 
⏩专栏分类:八大排序专栏⏪
 
?代码仓库:NEO的学习日记?
 
?关注我?带你学习排序知识
  ??

1. 前言?

博主第一次听见这个排序的时候
只觉得它很嚣张.别人都叫:
插入,希尔,归并排序,凭什么你叫快排
你到底有多快?心里是这个表情

但是当我学习完快排的思想
并且用三种方法写出代码后
博主只想说这是什么神仙思想
想出此方法的人定非 常人也!

废话不多说,上硬菜!

2. 快速排序基本思想?

基本思想:

• 从待排序的数组中选取一个基准值.
  (我们把基准值记为key)

• 再将数组分为两部分:
  1. 左子数组所有元素小于基准值
  2. 右子数组所有元素大于基准值

• 左右子数组再选基准值重复这个过程

对基准值选取的思考:

一般把数组第一个或
最后一个元素作为基准值
但是这样做有一定的缺陷
后面遇见问题了再修正

3. 快排思想实现(hoare版本)?

hoare版本:(发明者叫:C. A. R. Hoare )
也就是发明快排的人想出的方法

我们先定义一个无序数组:

int a[10]={6,1,2,7,9,3,4,5,10,8};

思路详解:

1. 将第一个元素6作为基准值
2. 定义两个指针指向:第一和最后的位置
3. 左边的指针(L)找比基准值大的值
4. 右边的指针( R)找比基准值小的值
5. R先走.R找到满足要求的值后停下
6. L再走,找到满足要求的值后停下
7. 当L和R都停下,交换两个位置数据
8. 当L和R相等时:
交换当前位置与基准值的值.

听起来比较抽象,我们画图理解一下:

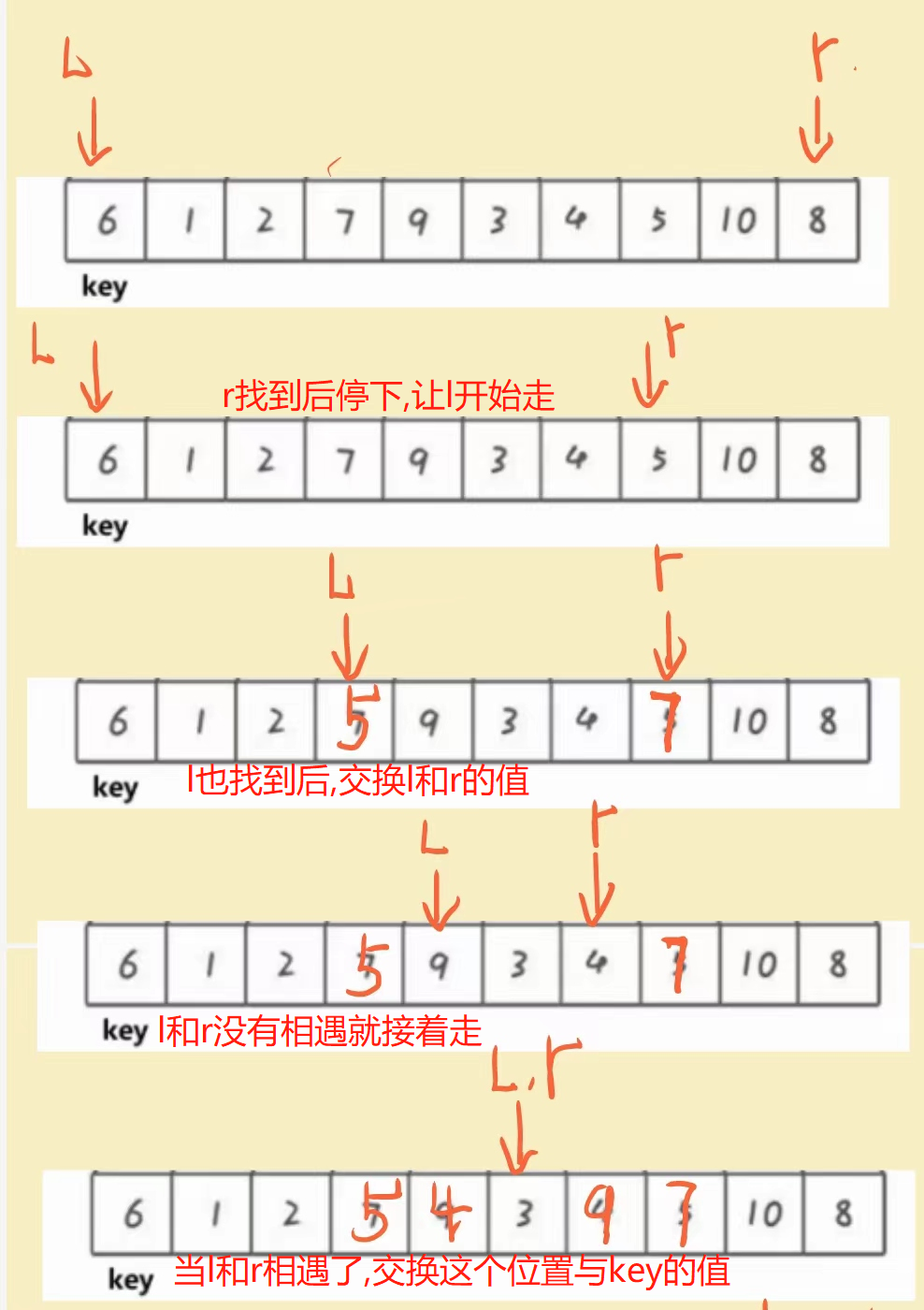
走完一次循环后,数组变成了这样:

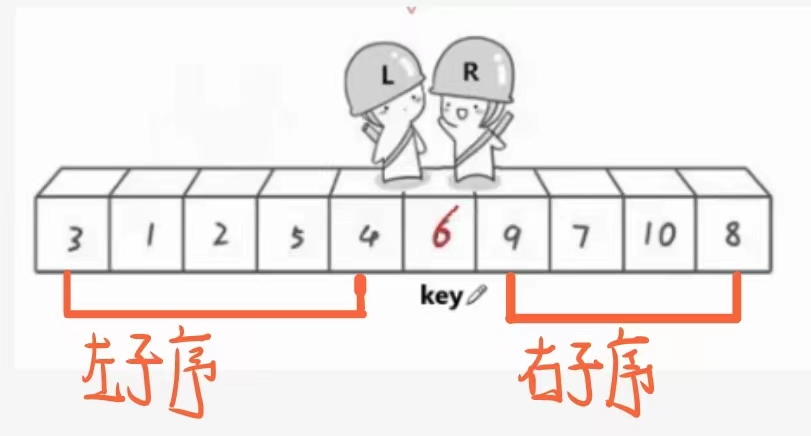
基准值的左边全部小于它
基准值的右边全部大于它

这说明这个基准值6
已经放在了数组中的正确位置!
也就是最终排好序的位置

我们只要不断递归左右子数组
最终这个数组就会变成有序!

4. 对hoare版本思路的解释?

思考:

1. l 和 r 相遇点的值会不会比key大?
   (这样交换后,key的左子序有值大于key了)
2. 最右的元素做key的步骤是什么?

解释:

1. 左边当基准值,右边先走

r 会寻找到比key小的值后停下来
停下来后 l 再走.当 l 和 r 都停下
并且 l 不等于 r时会交换它们的值
 
所以 l 和 r相遇的地方
只有两种可能

1. r 停下的位置,值比key小
2. 初始位置,值与key相同
   (当数组中所有值都比key大时)
   ( l 和 r会在初始位置相遇)

2. 步骤: 右边当基准值,左边先走

步骤和左边做基准值很像
左边先走,l 找大于key的值
找到后停下来右边再走
当 l 和 r 都停下并且它们不相等时
交换 l 和 r 所在位置的值
 
注意不一样的来了:
当 l 和 r 相遇后:
将当前位置的下一个位置的值
与基准值交换

拓展:
上面同时也解释了为什么:
左边做key要右边先走
右边做key要左边先走

5. 单趟快排代码实现?

void Partion(int* a, int left, int right)
{
	int key = left;
	while (left < right)
	{
		//右边先走,找小
		while (left < right && a[right] >= a[key])
		{
			right--;
		}
		//左边再走,找大
		while (left < right && a[left] <= a[key])
		{
			left++;
		}
		//左右都停下了,交换
		Swap(&a[left], &a[right]);
	}
	//当left和right相遇,交换此位置和key的值
	Swap(&a[left], &a[right]);
}

这里需要注意的是:

内层的while循环条件要加上:
left < right.不加上可能会越界

6. 快排递归实现?

因为实现单趟快排的函数
不好自身递归,所以我们需要
重新写一个函数来包含这个递归过程:

//快速排序
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	int key = Partion(a, left, right);
	QuickSort(a, left, key - 1);//递归左子序列
	QuickSort(a, key + 1, right);//递归右子序列
}

这里单趟快排函数Partion
需要个返回值返回l和r的相遇点

int Partion(int* a, int left, int right)
{
	int key = left;
	while (left < right)
	{
		//左边为key,那么右边先走,找小
		while (a[right] >= a[key] && left < right)
		{
			right--;
		}
		//左边后走,找大
		while (a[left] <= a[key] && left < right)
		{
			left++;
		}
		swap(&a[left], &a[right]);
	}
	swap(&a[left], &a[key]);//将key位置和左右相遇的位置交换
	return left;//将左或者右的值返回去当下一次递归的头或尾
}

7. 快排缺陷以及优化?

快排缺陷:

当原数组已经有序时
再使用快排可能会导致栈溢出
(报错为:StackOverflow)

因为指针 r 每次都走完了全部元素

一共要走:N+(N-1)+(N-2)+...+1次

时间复杂度为: O(N^2)

快排面对有序数组的问题
实际上是选取的key是数组的
最大值或最小值产生的.

快排优化:

要解决快排面对有序序列
递归次数过多的问题.
实际上就是解决在有序序列
选基准值key的问题

解决方法:

三数取中法:

从最左,最右和中间的元素中
选取一个既不是最大也不是最小的
元素做基准值key.
选好后都将它与最左边的值交换
相当于还是用最左边做key.
只不过这个key不会选到最大或最小数

代码实现:

int GetMidIndex(int* a, int left, int right)//三数取中,返回中间值
{
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

写出快速排序优化后的完整版代码:

//单趟快排(hoare版本)
int Partion(int* a, int left, int right)
{
	//三数取中--面对有序的情况不会栈溢出(key不会选到最大或者最小的数)
	int mini = GetMidIndex(a, left, right);
	swap(&a[left], &a[mini]);//交换三数取中的值与最左边的值
	int key = left;//基准值还是最左边的元素
	while (left < right)
	{
		//左边为key,那么右边先走,找小
		while (a[right] >= a[key] && left < right)
		{
			right--;
		}
		//左边后走,找大
		while (a[left] <= a[key] && left < right)
		{
			left++;
		}
		swap(&a[left], &a[right]);
	}
	swap(&a[left], &a[key]);//将key位置和左右相遇的位置交换
	return left;//将左或者右的值返回去当下一次递归的头或尾
}

//快速排序
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	int key = Partion(a, left, right);
	QuickSort(a, left, key - 1);
	QuickSort(a, key + 1, right);
}

8. 效率分析以及拓展?

时间复杂度分析:

1. 单趟次数:

单趟快排的时间复杂度比较好算:
指针 l 和 r走遍数组也就是走 n 次
时间复杂度为: O(N)

2. 总共趟数

在理想情况下,理想情况指:
每次选基准值key都接近中位数.
这种情况下类似于二叉树拆分
一共要走 log₂n趟.
时间复杂度为: O(logn)

3. 快排总的效率:

时间复杂度为: O(N*log₂N)

拓展:

既然快排有hoare版本
那肯定就有其他版本:

1. 挖坑法
2. 前后指针法

这都是国内的大佬想出来的办法

然而不管是hoare,挖坑,前后指针法
都是使用递归的手段解决问题
还有一种方法:
快排非递归法它可以解决栈溢出的问题

前面所有的方法都会一一给大家分享?

快排不能使用的场景:

就算快排再快,并且做了三数取中优化
但遇见全是重复数字的数组效率也非常低!
如果你提前知道待排序序列中
很多都是重复的数字,那么
你应该避免使用快速排序.

快速排序再快
也有排不了的序列
就像:
再快的AE86也追不回
坐在奔驰车上的夏树