您现在的位置是:首页 >技术教程 >模拟退火算法(SA)解决函数极值和TSP问题(matlab和python代码)网站首页技术教程
模拟退火算法(SA)解决函数极值和TSP问题(matlab和python代码)
模拟退火算法
模拟退火算法 (SA)的思想最早由Metropolis等人于1953年提出。Kirkpatrick等人于1983年第一次使用模拟退火算法求解组合最优化问题。模拟退火算法是一种基于Monte Carlo迭代求解策略的随机寻优算法,基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。其目的在于:为具有NP-hard复杂性的问题提供有效的近似求解算法,克服传统算法优化过程容易陷入局部极值的缺陷和对初值的依赖性(如爬山法)。
模拟退火算法是一种通用的智能优化算法,全局搜索性能和局部搜索性能较优,因其用了许多独特的方法和技术:基本不用搜索空间的知识或者其他辅助信息,而只是定义邻域结构,在邻域结构内选取相邻解,再利用目标函数进行评估;采用概率的变迁来指导它的搜索方向,它所采用的概率仅仅是作为一种工具来引导其搜索过程朝着更优化解的区域移动。因此,虽然看起来它是一种盲目的搜索方法,但实际上有着明确的搜索方向。
模拟退火原理
模拟退火算法的优化问题求解过程与物理退火过程之间极其相似,优化的目标函数相当于金属的内能,优化问题的自变量组合状态空间相当于金属的内能状态空间,问题的求解过程就是找一个组合状态,使目标函数值最小。利用Metopolis算法并适当地控制温度的下降过程实现模拟退火,从而达到求解全局优化问题的目的。
模拟退火算法与金属退火过程的关系对比
| 物理退火 | 模拟退火 |
|---|---|
| 粒子状态 | 解 |
| 能量最低态 | 最优解 |
| 溶解过程 | 设定初温 |
| 等温过程 | Metropolis采样过程 |
| 冷却 | 控制参数温度T的下降 |
| 能量 | 目标函数 |
模拟退火算法流程图

模拟退火算法主要思想
在搜索区间随机游走(即随机选择点),再利用Metropolis抽样准则,使随机游走逐渐收敛于局部最优解。而温度是Metropolis算法中的一个重要控制参数,可以认为这个参数的大小控制了随机过程向局部或全局最优解移动的快慢。
Metropolis 是一种有效的重点抽样法,其算法为:系统从一个能量状态变化到另一个状态时,相应的能量从E1变化到E2,其概率为:
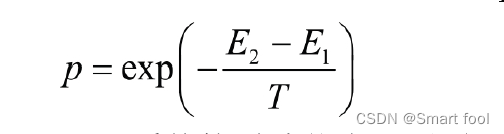
如果E2<E1,系统接受此状态;否则,以一个随机的概率接受或丢弃此状态。状态2被接受的概率为

这样经过一定次数的迭代,系统会逐渐趋于一个稳定的分布状。
模拟算法的特点:
1、以一定的概率接受劣解: 主要是上述两个公式, Metropolis 采样法,将温度作为控制参数,开始时温度T值大,可以接受较差的劣解;随着温度T的减小,只能接受较好的劣解,最后在T趋于0时,就不再接受任何劣解了。
2、引进算法控制参数:引进类似于退火温度的算法控制参数,它将优化过程分成若干阶段,并决定各个阶段下随机状态的取舍标准,接受函数由Metropolis算法给出一个简单的数学模型。模拟退火算法有两个重要的步骤:是在每个控制参数下,由前迭代点出发,产生邻近的随机状态,由控制参数确定的接受准则决定此新状态的取舍,并由此形成一定长度的随机Markov链;二是缓慢降低控制参数,提高接受准则,直至控制参数趋于零,状态链稳定于优化问题的最优状态,从而提高模拟退火算法全局最优解的可靠性。
3、对目标函数要求较少:而模拟退火算法不需要其他的辅助信息,而只是定义邻域结构,在其邻域结构内选取相邻解,再用目标函数进行评估。
算法理解:
SA算法最主要的过程和理解就是Metropolis采样。求函数极值问题时将函数值作为物理退火中的能量问题。在解决TSP问题时,主要是随机选择置换两个不同的城市的坐标。算法可以从以下几个方面改进: 增加记忆存储环节,迭代过程中将目前为止最好的状态存储下来;增加升温和重升温过程,避免算法在局部极小值解解处停滞不前;由于SA算法采用双循环,算法运行效率较低,可以与其余算法如GA和免疫算法结合,提高运行效率和求解质量。
本文主要是为了学习SA算法解决函数极值和TSP问题,了解SA算法运行原理,并通过借鉴和参考其余博主代码和博客内容,提高自身编程能力和算法知识水平。若有错误还望大家批评指正!
资料来源:
1、https://zhuanlan.zhihu.com/p/609164889#%E6%A8%A1%E6%8B%9F%E9%80%80%E7%81%AB%E7%AE%97%E6%B3%95%E8%A7%A3%E5%86%B3TSP%E9%97%AE%E9%A2%98
2、包子阳,余继周,等,智能优化算法及其MATLAB实例(第二版),电子工业出版社。
3、https://blog.csdn.net/weixin_43935696/article/details/107045716
4、https://zhuanlan.zhihu.com/p/266874840
为了更好的了解SA算法的Metropolis 采样过程,与爬山法进行对比:
通过代码,发现爬山法能否找到最值和初值选取密切相关,大多数时候只能找到极值,因为迭代是每次向着领域内移动。
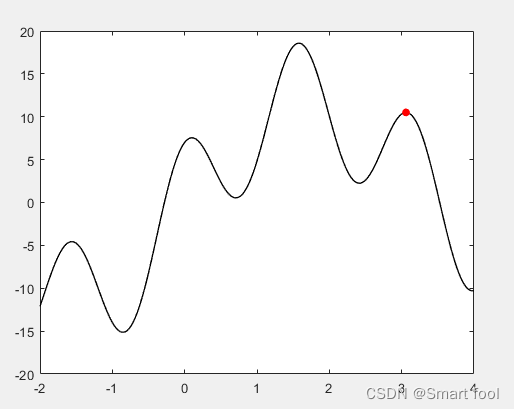
% 爬山法代码
clc;clear ;close all
x=-2:0.01:4;
y=x+10*sin(x)+7*cos(4*x);
plot(x,y,'k','LineWidth',1.5)
title('y=x+10sinx+7cos(4x)')
xlabel('X')
ylabel('Y')
grid on
hold on
%初始化参数
xlim=[min(x),max(x)];%定义域
k=1000;%最大迭代次数
xstar=xlim(1)+(xlim(2)-xlim(1))*rand;%生成初始解并认为是初始最优解
ystar=xstar+10*sin(xstar)+7*cos(4*xstar);%生成初始解的值
for i=1:k
%领域结构设计,这儿领域结构采用的当前最优解向左减去0.1到向右加上0.1的区间
if xstar-0.1>=xlim(1)&&xstar+0.1<=xlim(2)
xnew=xstar+(-0.1)+0.2*rand;
elseif xstar-0.1<xlim(1)
xnew=xstar+0.1*rand;
else
xnew=xstar-0.1*rand;
end
ynew=xnew+10*sin(xnew)+7*cos(4*xnew);
if ynew>ystar
xstar=xnew;
ystar=ynew;%如果生成的领域解的值大于当前最优解,就更新当前最优解
end
% 增加粒子状态动态变化的过程
plot(x,y,'k',xstar,ystar,'r.','LineWidth',1,'MarkerSize',20)
hold off
pause(0.01)
end
SA算法解决函数极值问题,并增加粒子状态动态变化过程
 
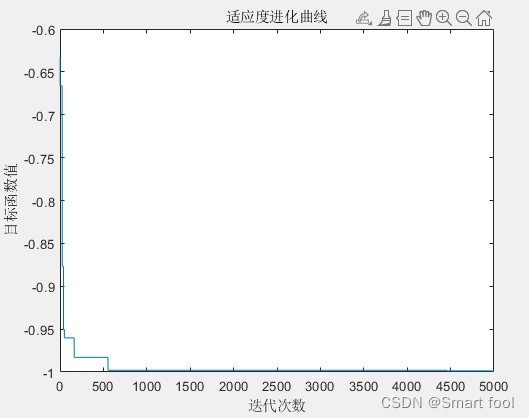
clc;clear ;close all
%%原始数据图像
x=0.5:0.1:2*pi-0.5;
[x,y]=meshgrid(x); %生成平面网格坐标矩阵
z=sin(y).*cos(x);
mesh(x,y,z); %绘制曲面
xlabel('x'); %标明x轴名字
ylabel('y');
zlabel('z');
hold on
%%SA算法
%初始化参数
D = 2; % 变量维度
Xs =2*pi-0.5;%%函数上限
Xx =0.5;%%函数下限
%%%%%%%%%%%%%%%%%%%%冷却表参数%%%%%%%%%%%%%%%%%%%%%%%%%%
L= 100; %马尔可夫链长度
K = 0.9; %衰减参数
S = 0.1; %步长因子,就是每次解变化的大小
T = 100; % 初始温度
YZ = 1e-8; %容差
P = 0; %Metropolis过程接受点
%%%%%%%%%%%%%%%%%随机选点初值设定%%%%%%%%%%%%%%%%%%%5
PreX = rand(D,1)*(Xs-Xx)+Xx;%初始化矩阵D × 1的解
PreBestX = PreX;%用于保存上一个最优的解
PreX = rand(D,1)*(Xs-Xx)+Xx;
BestX = PreX;%用于保存当前最优解
%%%%%%%%%%%%%%%%%每迭代一次退火一次(降温),直到满足迭代条件为止%%%%%%%%%
deta = abs(func1(BestX)-func1(PreBestX));%能量差值,适应度差值
while (deta>YZ) && (T>0.001)
T = K*T;%%降温
%%%%%%%%%%%%在当前温度T下迭代次数%%%%%%%%%%%%
for i = 1:L
%%%%%%%%%%%%在此点附近随机选择下一点%%%%%%%%%%%%%%%
%%%%%%%%%%%%根据当前条件产生一个新解%%%%%%%%%%%%%%%%%
NextX = (rand(D,1) * (Xs-Xx)+Xx);
%%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%
%%%%%%%%%%%%%%因为上一行代码是随机产生的数,判断产生的数,是否超过定义域范围,超过则重新产生一个数%%%%%%
for ii = 1:D
if NextX(ii) > Xs | NextX(ii) < Xx
NextX(ii) = PreX(ii) + S* (rand * (Xs-Xx)+Xx);
end
end
%%%%%%%%%%%%%%是否全局最优解%%%%%%%%%%%%%%%%%%%%
if (func1(BestX) > func1(NextX))
%%%%%%%%%%%%%%%%%%%%保留上一个最优解%%%%%%%%%%%%%%5
PreBestX = BestX;
%%%%%%%%%%%%%%%%%此为新的最优解%%%%%%%%%%%%%%%%%
BestX = NextX;
end
%%%%%%%%%%%%%%%Metropolis过程%%%%%%%%%%%%%%%%%%%
if(func1(PreX) - func1(NextX)>0)
%%%%%%%%%%%%%%接受新解%%%%%%%%%%%%%
PreX = NextX;
P = P+1;
else
%%%%%%%%%%%%%%%%%%%求状态2接受的概率接受新解%%%%
%%%%%%%%%%%%%%%%%%%随着越来越接近最优值的时候,接受较差的状态的概率越低%%%%%
changer = -1 * (func1(NextX)-func1(PreX))/T;
p1 = exp(changer);
%%%%%%%%%%%%%%%%%%以一定概率接受较差的解%%%%%%%%%%%%%%%%%
if p1 >rand
PreX = NextX;
P =P+1;
end
end
trace(P+1) = func1(BestX);
end
deta = abs(func1(BestX) - func1(PreBestX));
scatter3(BestX(1),BestX(2), trace(P+1),'r*');
hold on
pause(0.001)
end
%最小值的解
BestX
%解的适应度
func1(BestX)
figure
plot(trace(2:end))
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
%%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%
function result = func1(x)
result = sin(x(2)).*cos(x(1));
end
SA算法解决TSP问题


; %TSP问题的规模,即城市数目
T=100*n; %初始温度
L=100; %马尔科夫链的长度
K=0.99; %衰减参数
%%%城市坐标结构体%%%%%%%
city=struct([]);
for i=1:n
city(i).x=C(i,1);
city(i).y=C(i,2);
end
l=1; %统计迭代次数
len(l)=func5(city,n); %每次迭代后路线的长度
figure(1);
while T>0.001
%%%%%%%%%%%%%%%多次迭代扰动,温度降低前多次试验%%%%%%%%
for i=1:L
%%%%%%%%%%%%%%%计算原路线总距离%%%%%%%%%
len1=func5(city,n);
%%%%%%%%%%%%%%%产生随机扰动%%%%%%%%%
%%%%%%%%%%%%%%%随机置换两个不同的城市的坐标%%%%%%%%%
p1=floor(1+n*rand);
p2=floor(1+n*rand);
while p1==p2
p1=floor(1+n*rand);
p2=floor(1+n*rand);
end
tmp_city=city;
%%交换元素
tmp=tmp_city(p1);
tmp_city(p1)=tmp_city(p2);
tmp_city(p2)=tmp;
%%%%%%%%%%%%%%%计算新路线总距离%%%%%%%%%
len2=func5(tmp_city,n);
%%%%%%%%%%%%%%%新老距离的差值,相当于能量%%%%%%%%%
delta_e=len2-len1;
%%%%%%%%%%%%%%%新路线好于旧路线,用新路线替代旧路线%%%%%%%%%
if delta_e<0
city=tmp_city;
else
%%%%%%%%%%%%%%%以一定概率选择是否接受%%%%%%%%%
if exp(-abs(delta_e/T))>rand()
city=tmp_city;
end
end
end
l=l+1; %迭代次数加1
%%%%%%%%%%%%%%%计算新路线的距离%%%%%%%%%
len(l)=func5(city,n);
%%%%%%%%%%%%%%%温度不断下降%%%%%%%%%
T=T*K;
for i=1:n-1
plot([city(i).x,city(i+1).x],[city(i).y,city(i+1).y],'bo-');
hold on;
end
plot([city(n).x,city(1).x],[city(n).y,city(1).y],'ro-');
title(['优化最短距离:',num2str(len(l))]);%%num2str将数字转为字符数组
hold off;
pause(0.005);
end
figure(2)
plot(len);
xlabel('迭代次数');
ylabel('目标函数值');
title('适应度进化曲线');
%计算距离的函数
function len=func5(city,n)
len=0;
for i=1:n-1
len=len+sqrt((city(i).x-city(i+1).x)^2+(city(i).y-city(i+1).y)^2);
end
len=len+sqrt((city(n).x-city(1).x)^2+(city(n).y-city(1).y)^2);
end
python代码后续再补充,持续学习中






 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结