目录

1 引言：

1 数据压缩的重要性和应用场景

2 压缩算法的基本原理和分类

2. 无损压缩算法

2.1 哈夫曼编码

2.1.1 哈夫曼编码的原理和步骤

2.1.2 实现一个简单的哈夫曼编码器

2.2 字典编码

2.2.1 LZW算法的原理和步骤

2.2.2 实现一个基于LZW算法的压缩程序

2.3 预测编码

2.3.1 算术编码的原理和实现

2.3.2 差分编码的原理和实现

3. 有损压缩算法

3.1 转换编码

3.1.1 傅里叶变换在图像压缩中的应用

3.1.2 实现一个基于DCT的JPEG压缩程序

3.2 量化

3.2.1 图像颜色深度的降低与压缩

3.2.2 音频采样率的降低与压缩

3.3 基于模型的压缩

3.3.1 视频压缩中的帧间压缩算法

3.3.2 实现一个简单的视频压缩程序

4. 压缩算法的效果评估与比较

4.1 压缩比率、解压速度和质量损失的衡量指标

4.2 常见压缩算法的效果比较

5. 压缩算法的应用和发展趋势

5.1 图像、音频和视频压缩的应用场景

5.2 压缩算法的新进展和研究方向

6. 总结

6.1 对压缩算法的综述和总结

6.2 对未来压缩算法发展的展望

---

1 引言：

1 数据压缩的重要性和应用场景

        数据压缩是计算机领域中一项重要的技术，它可以将数据在占用更小的存储空间或通过更低的传输带宽进行表示和传输。数据压缩的重要性源于以下几个方面：

1. 节省存储空间：随着数据的不断增长，存储空间成为一项宝贵的资源。通过压缩数据，可以显著减少存储设备的使用量，从而降低存储成本并提高数据管理的效率。

2. 提高数据传输效率：在数据通信领域，传输带宽是一个宝贵的资源。通过压缩数据，可以减少传输数据的大小，从而降低传输延迟和成本，并提高数据传输的效率。

3. 数据备份和归档：压缩数据可以减少备份和归档操作所需的存储空间和传输时间。这对于保护和长期保存数据至关重要。

4. 提高系统性能：压缩数据可以降低数据访问和处理的时间，提高系统的响应速度和性能。

2 压缩算法的基本原理和分类

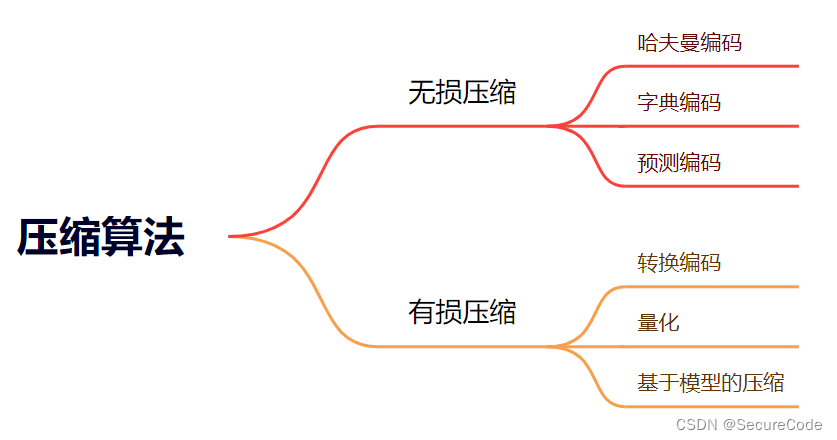
        压缩算法基于对数据的统计特性和重复模式的利用，可以分为两大类：无损压缩算法和有损压缩算法。

1. 无损压缩算法： 无损压缩算法通过消除数据中的冗余和重复部分来压缩数据，同时保持数据的完整性和准确性。常见的无损压缩算法包括：

   • 哈夫曼编码：通过构建变长编码表，将频率高的符号用较短的编码表示，频率低的符号用较长的编码表示，从而实现无损压缩。
   • 字典编码：根据数据中出现的字典词汇进行编码，将连续出现的词汇表示为一个编码，从而实现无损压缩。常见的字典编码算法包括LZW算法和LZ77算法。
   • 预测编码：基于数据的统计特性和预测模型，将数据表示为预测误差和预测模型参数的编码，从而实现无损压缩。常见的预测编码算法包括算术编码和差分编码。

2. 有损压缩算法： 有损压缩算法通过舍弃数据中的一些细节和冗余信息来实现更高的压缩率，但会引入一定程度的信息损失。有损压缩算法主要应用于图像、音频和视频等多媒体数据的压缩。常见的有损压缩算法包括：

   • 转换编码：通过将数据转换到一种新的表示形式，例如傅里叶变换或离散余弦变换，然后舍弃高频部分的细节信息来实现压缩。
   • 量化：通过减少数据的精度或采样率来实现压缩，例如减少图像的颜色深度或音频的采样率。
   • 基于模型的压缩：利用数据的统计模型或预测模型，对数据进行编码和压缩，例如视频压缩中的帧间压缩算法。

        数据压缩在计算机领域中具有重要的应用价值。无损压缩算法可以实现对数据的完整性保持，适用于文本和一些需要保留精确信息的数据。有损压缩算法可以在一定程度上降低数据的质量，但在多媒体数据的压缩和传输中具有广泛的应用。

2. 无损压缩算法

2.1 哈夫曼编码

2.1.1 哈夫曼编码的原理和步骤

        哈夫曼编码是一种常用的无损压缩算法，它通过构建最优前缀编码来实现数据的压缩。哈夫曼编码的原理是根据符号出现的频率来构建一个最优的二叉树（哈夫曼树），并将出现频率高的符号用较短的编码表示，出现频率低的符号用较长的编码表示。

步骤：

1. 统计输入数据中每个符号的出现频率。
2. 根据频率构建哈夫曼树。首先创建一个包含所有符号的叶子节点集合，每个节点的权重为符号的频率。然后重复以下步骤直到只剩下一个根节点：
   • 从节点集合中选择两个权重最小的节点，作为左右子节点创建一个新的父节点。
   • 将新节点的权重设为左右子节点权重之和。
   • 将新节点加入节点集合。
   • 从节点集合中删除原先选出的两个节点。
3. 根据哈夫曼树为每个符号分配唯一的编码。从根节点出发，沿着左子树走为0，沿着右子树走为1，记录下路径上的0和1即为符号的编码。
4. 使用生成的编码对输入数据进行压缩。将每个符号替换为对应的编码。
5. 将压缩后的数据以及编码表（记录每个符号的编码）一起保存，以便解压缩时使用。

2.1.2 实现一个简单的哈夫曼编码器

        实现一个简单的哈夫曼编码器可以按照以上步骤进行编码和解码的过程。具体实现时需要考虑编码表的存储方式、对输入数据进行编码和解码的逻辑等。

以下是一个简单的哈夫曼编码器的示例代码：

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int symbol;           // 符号
    int frequency;        // 频率
    struct Node* left;    // 左子节点
    struct Node* right;   // 右子节点
} Node;

// 创建一个新的节点
Node* createNode(int symbol, int frequency) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->symbol = symbol;
    newNode->frequency = frequency;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// 交换节点
void swapNodes(Node** arr, int i, int j) {
    Node* temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// 将数组转化为最小堆
void heapify(Node** arr, int n, int i) {
    int smallest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;

    if (left < n && arr[left]->frequency < arr[smallest]->frequency)
        smallest = left;

    if (right < n && arr[right]->frequency < arr[smallest]->frequency)
        smallest = right;

    if (smallest != i) {
        swapNodes(arr, i, smallest);
        heapify(arr, n, smallest);
    }
}

// 构建最小堆
void buildMinHeap(Node** arr, int n) {
    int i;
    for (i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
}

// 提取最小节点
Node* extractMin(Node** arr, int* n) {
    Node* minNode = arr[0];
    arr[0] = arr[*n - 1];
    (*n)--;
    heapify(arr, *n, 0);
    return minNode;
}

// 插入节点到最小堆
void insertMinHeap(Node** arr, int* n, Node* newNode) {
    (*n)++;
    int i = *n - 1;
    while (i > 0 && newNode->frequency < arr[(i - 1) / 2]->frequency) {
        arr[i] = arr[(i - 1) / 2];
        i = (i - 1) / 2;
    }
    arr[i] = newNode;
}

// 生成哈夫曼编码
void generateCodes(Node* root, int* codes, int top) {
    if (root->left) {
        codes[top] = 0;
        generateCodes(root->left, codes, top + 1);
    }

    if (root->right) {
        codes[top] = 1;
        generateCodes(root->right, codes, top + 1);
    }

    if (!root->left && !root->right) {
        printf("符号: %d, 编码: ", root->symbol);
        for (int i = 0; i < top; i++) {
            printf("%d", codes[i]);
        }
        printf("
");
    }
}

// 哈夫曼编码的压缩函数
void encode(FILE* inputFile, FILE* outputFile) {
    // 步骤1：统计输入文件中每个符号的频率
    int frequency[256] = {0};
    int symbol;
    while ((symbol = fgetc(inputFile)) != EOF) {
        frequency[symbol]++;
    }

    // 步骤2：构建最小堆
    int n = 0;
    Node* minHeap[256];
    for (int i = 0; i < 256; i++) {
        if (frequency[i] > 0) {
            minHeap[n] = createNode(i, frequency[i]);
            n++;
        }
    }
    buildMinHeap(minHeap, n);

    // 步骤3：构建哈夫曼树
    while (n > 1) {
        Node* left = extractMin(minHeap, &n);
        Node* right = extractMin(minHeap, &n);

        Node* newNode = createNode(-1, left->frequency + right->frequency);
        newNode->left = left;
        newNode->right = right;

        insertMinHeap(minHeap, &n, newNode);
    }

    // 步骤4：生成哈夫曼编码
    int codes[256];
    generateCodes(minHeap[0], codes, 0);

    // 步骤5：使用哈夫曼编码对输入文件进行编码
    fseek(inputFile, 0, SEEK_SET);
    int bitBuffer = 0;
    int bitsInBuffer = 0;

    while ((symbol = fgetc(inputFile)) != EOF) {
        for (int i = 0; i < top; i++) {
            bitBuffer = (bitBuffer << 1) | codes[symbol][i];
            bitsInBuffer++;

            if (bitsInBuffer == 8) {
                fputc(bitBuffer, outputFile);
                bitBuffer = 0;
                bitsInBuffer = 0;
            }
        }
    }

    // 将缓冲区中剩余的位写入文件
    if (bitsInBuffer > 0) {
        bitBuffer = bitBuffer << (8 - bitsInBuffer);
        fputc(bitBuffer, outputFile);
    }
}

// 哈夫曼编码的解压函数
void decode(FILE* inputFile, FILE* outputFile) {
    // 步骤1：从输入文件中读取哈夫曼树
    Node* root = createNode(-1, 0);

    int bit;
    Node* currentNode = root;

    while ((bit = fgetc(inputFile)) != EOF) {
        if (bit == '0') {
            if (!currentNode->left) {
                currentNode->left = createNode(-1, 0);
            }
            currentNode = currentNode->left;
        } else {
            if (!currentNode->right) {
                currentNode->right = createNode(-1, 0);
            }
            currentNode = currentNode->right;
        }

        if (!currentNode->left && !currentNode->right) {
            fputc(currentNode->symbol, outputFile);
            currentNode = root;
        }
    }

    // 步骤2：使用哈夫曼树解码编码的数据
}

int main() {
    FILE* inputFile = fopen("input.txt", "r");
    FILE* encodedFile = fopen("encoded.bin", "wb");

    encode(inputFile, encodedFile);

    fclose(inputFile);
    fclose(encodedFile);

    return 0;
}

        上述代码是一个简单的哈夫曼编码器的实现。它通过统计输入文件中每个符号的出现频率，并根据频率构建哈夫曼树。然后根据哈夫曼树为每个符号生成唯一的编码，并使用编码对输入文件进行压缩。解压缩时，根据保存的哈夫曼树进行解码操作，将编码还原为原始数据。

2.2 字典编码

        LZW（Lempel-Ziv-Welch）算法是一种常用的字典编码算法，用于数据压缩。它通过动态构建和更新字典来实现数据的压缩和解压缩。下面将介绍LZW算法的原理和步骤，并给出一个基于LZW算法的压缩程序的实现。

2.2.1 LZW算法的原理和步骤

        LZW算法的核心思想是利用输入数据中的重复模式来构建字典，并用较短的编码代表较长的模式，从而实现数据的压缩。

LZW算法的步骤如下：

1. 初始化字典：创建一个初始字典，其中包含所有可能的输入符号。

2. 输入处理：读取输入数据，并将第一个输入符号作为当前模式。

3. 模式匹配和字典更新：从输入中读取下一个符号，并将当前模式与已有字典中的模式进行匹配。

   • 如果匹配成功，将当前模式与下一个输入符号拼接，得到一个新的模式，继续进行匹配。
   • 如果匹配失败，将当前模式的编码输出，并将当前模式与下一个输入符号作为新的模式。

4. 编码输出：将最后一个匹配成功的模式的编码输出。

5. 字典更新：将最后一个匹配成功的模式与下一个输入符号拼接，将这个新的模式添加到字典中。

6. 重复步骤3-5，直到所有输入数据被处理完毕。

2.2.2 实现一个基于LZW算法的压缩程序

下面是一个基于LZW算法的压缩程序的简单实现，使用C语言编写：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_DICT_SIZE 4096

typedef struct {
    int code;
    char* pattern;
} Entry;

void compress(FILE* inputFile, FILE* outputFile) {
    Entry dict[MAX_DICT_SIZE];
    int dictSize = 256;  // 初始字典大小为256，表示ASCII字符

    // 初始化字典
    for (int i = 0; i < 256; i++) {
        dict[i].code = i;
        dict[i].pattern = (char*)malloc(2 * sizeof(char));
        dict[i].pattern[0] = (char)i;
        dict[i].pattern[1] = '';
    }

    int currentCode = 0;
    char currentSymbol;
    char nextSymbol;
    char* currentPattern = (char*)malloc(2 * sizeof(char));
    currentPattern[0] = fgetc(inputFile);
    currentPattern[1] = '';

    while ((nextSymbol = fgetc(inputFile)) != EOF) {
        char* nextPattern = (char*)malloc((strlen(currentPattern) + 2) * sizeof(char));
        strcpy(nextPattern, currentPattern);
        strncat(nextPattern, &nextSymbol, 1);

        int found = 0;
        for (int i = 0; i < dictSize; i++) {
            if (strcmp(dict[i].pattern, nextPattern) == 0) {
                currentPattern = nextPattern;
                found = 1;
                break;
            }
        }

        if (!found) {
            fwrite(&dict[currentCode].code, sizeof(int), 1, outputFile);

            if (dictSize < MAX_DICT_SIZE) {
                dict[dictSize].code = dictSize;
                dict[dictSize].pattern = (char*)malloc((strlen(nextPattern) + 1) * sizeof(char));
                strcpy(dict[dictSize].pattern, nextPattern);
                dictSize++;
            }

            currentPattern = (char*)malloc(2 * sizeof(char));
            currentPattern[0] = nextSymbol;
            currentPattern[1] = '';

            currentCode = nextSymbol;
        }
    }

    fwrite(&dict[currentCode].code, sizeof(int), 1, outputFile);

    // 释放内存
    for (int i = 0; i < dictSize; i++) {
        free(dict[i].pattern);
    }
    free(currentPattern);
}

int main() {
    FILE* inputFile = fopen("input.txt", "r");
    FILE* compressedFile = fopen("compressed.bin", "wb");

    compress(inputFile, compressedFile);

    fclose(inputFile);
    fclose(compressedFile);

    return 0;
}

        上述代码实现了一个简单的基于LZW算法的压缩程序。它通过读取输入文件中的字符，并根据LZW算法进行编码，将编码后的数据写入输出文件。压缩程序使用一个字典来存储已有的模式，并根据模式的匹配情况进行编码输出和字典的更新。需要注意的是，上述代码中的字典大小限定为最大4096个条目，当字典达到这个大小时，压缩程序不再更新字典，而是继续进行编码输出。

2.3 预测编码

        预测编码是一种无损压缩算法，它利用数据的统计特性和预测模型来减少数据的冗余。预测编码算法会根据已有的数据进行预测，并根据预测结果进行编码。常见的预测编码算法包括算术编码和差分编码。

2.3.1 算术编码的原理和实现

        算术编码是一种基于数据统计概率的预测编码算法，它将整个输入序列视为一个符号流，并根据每个符号出现的概率进行编码。算术编码的基本原理是将输入符号映射到一个区间，每个区间表示一个概率范围，然后根据输入符号的概率进行区间的缩放和更新。最后，编码器将输入序列映射到最终的编码区间。

算术编码的实现步骤如下：

1. 统计符号概率：通过分析输入数据，统计每个符号出现的概率。

2. 构建编码区间：将符号的概率映射到一个区间，通常使用累积概率分布来确定区间的大小和位置。例如，可以使用区间的上界和下界来表示编码区间。

3. 编码输入序列：对于输入的每个符号，根据符号的概率缩放和更新编码区间。可以根据符号的累积概率分布来确定缩放因子，并根据缩放后的区间更新编码区间。

4. 输出编码结果：最终的编码结果是输入序列对应的编码区间。可以使用二进制表示编码区间的上界或下界，并将编码结果输出。

2.3.2 差分编码的原理和实现

        差分编码是一种基于数据差分的预测编码算法，它利用当前数据与前一个数据之间的差异来进行编码。差分编码的基本原理是将每个数据与前一个数据进行差分运算，然后将差值进行编码。通过利用数据之间的相关性，差分编码可以减少数据的冗余。

差分编码的实现步骤如下：

1. 初始化：将前一个数据初始化为一个已知值，例如0或者输入数据的某个特定值。

2. 编码输入序列：对于输入的每个数据，计算当前数据与前一个数据的差值，并将差值进行编码。可以使用任何合适的编码方法来表示差值，例如二进制编码。

3. 更新前一个数据：将当前数据作为下一个数据的前一个数据，以便下一次差分编码。

4. 输出编码结果：输出编码后的数据序列作为最终的编码结果。

        差分编码通常用于连续数据或时间序列数据的压缩，因为这些数据具有较强的相关性和连续性。通过差分编码，可以将数据序列转换为差分数据序列，从而减少数据的冗余和表示的位数。

        请注意，以上是算术编码和差分编码的基本原理和实现步骤的简要介绍，实际应用中可能需要考虑更多的细节和优化，并根据具体情况选择合适的参数和方法。

3. 有损压缩算法

3.1 转换编码

        转换编码是一种有损压缩算法，它将输入数据从原始域转换到另一个域，并利用转换后的数据特性来减少数据的冗余。转换编码算法通常适用于信号处理和图像压缩领域。常见的转换编码算法包括傅里叶变换、离散余弦变换（DCT）、小波变换等。

3.1.1 傅里叶变换在图像压缩中的应用

        傅里叶变换是一种将信号或图像从时域转换到频域的数学变换。在图像压缩中，傅里叶变换广泛应用于JPEG压缩算法中的频域编码部分。

        JPEG压缩算法使用了离散余弦变换（DCT），它是傅里叶变换的一种变体。DCT将图像分解为一系列频域成分，其中每个成分表示不同频率的变化。通过对这些频域成分进行量化和编码，可以实现图像的压缩。

JPEG压缩算法的基本步骤如下：

1. 将彩色图像转换为亮度和色度分量。对于彩色图像，首先将其转换为亮度（Y）和色度（Cb和Cr）分量，以便对亮度和色度进行独立的压缩。

2. 对每个分量进行图像分块。将亮度和色度分量划分为8x8的图像块。

3. 对每个图像块进行离散余弦变换（DCT）。对于每个8x8的图像块，应用离散余弦变换，将图像从空域转换到频域。

4. 对DCT系数进行量化。将DCT系数进行量化，减少高频成分的精度，从而实现数据的压缩。

5. 进行熵编码。对量化后的DCT系数进行熵编码，使用哈夫曼编码或其他熵编码算法来实现数据的进一步压缩。

6. 重构图像。解码器根据压缩数据和解码过程的逆操作，对量化系数进行逆量化和逆DCT变换，以重构原始图像。

3.1.2 实现一个基于DCT的JPEG压缩程序

        实现一个完整的JPEG压缩程序超出了本文档的范围，因为它涉及到多个复杂的步骤和算法。然而，以下是一个基于DCT的JPEG压缩程序的简单示例，用于演示DCT的应用：

# 导入所需的库
import numpy as np
from scipy.fftpack import dct

# 定义JPEG压缩函数
def jpeg_compress(image):
    # 将图像块划分为8x8的块
    blocks = image.reshape(-1, 8, 8)
    
    # 对每个图像块进行DCT变换
    dct_blocks = np.zeros_like(blocks)
    for i in range(blocks.shape[0]):
        dct_blocks[i] = dct(dct(blocks[i], axis=0), axis=1)
    
    # 对DCT系数进行量化
    quantized_blocks = np.round(dct_blocks / quantization_table)
    
    # 对量化后的系数进行熵编码等进一步压缩步骤
    
    # 返回压缩后的数据
    return quantized_blocks

# 定义量化表
quantization_table = np.array([
    [16, 11, 10, 16, 24, 40, 51, 61],
    [12, 12, 14, 19, 26, 58, 60, 55],
    [14, 13, 16, 24, 40, 57, 69, 56],
    [14, 17, 22, 29, 51, 87, 80, 62],
    [18, 22, 37, 56, 68, 109, 103, 77],
    [24, 35, 55, 64, 81, 104, 113, 92],
    [49, 64, 78, 87, 103, 121, 120, 101],
    [72, 92, 95, 98, 112, 100, 103, 99]
])

# 读取图像数据
image = read_image("input.jpg")

# 调用JPEG压缩函数
compressed_data = jpeg_compress(image)

# 保存压缩后的数据
save_compressed_data(compressed_data, "compressed.jpg")

        请注意，上述示例仅展示了DCT在JPEG压缩中的应用的基本步骤，实际的JPEG压缩程序需要考虑更多的细节和优化。

3.2 量化

        量化是一种有损压缩算法中常用的步骤，用于减少数据的精度以实现压缩。在图像和音频压缩中，量化可以降低颜色深度和采样率，从而减少数据的存储空间和传输带宽要求。

3.2.1 图像颜色深度的降低与压缩

        图像的颜色深度指的是图像中每个像素可以表示的颜色数量。常见的图像格式如RGB图像使用24位颜色深度，可以表示16777216种颜色（2^24）。降低图像的颜色深度可以减少每个像素所占用的存储空间，从而实现图像的压缩。

        一种常见的颜色深度降低方法是使用调色板（Palette）。调色板是一个包含有限颜色集合的表格，图像中的每个像素使用调色板中的索引值来表示其颜色。通过将图像中的每个像素映射到调色板中的索引值，可以将颜色深度从24位降低到较低的位数，从而减少图像的存储空间。

        例如，如果使用8位调色板，可以表示256种不同的颜色。对于每个像素，只需要存储一个8位的索引值，而不是原始的24位颜色值。这样，图像的存储空间可以大大减少，实现了图像的压缩。

3.2.2 音频采样率的降低与压缩

        音频的采样率指的是在一秒钟内对音频信号进行采样的次数。采样率决定了音频的音质和频谱范围，高采样率可以更准确地还原原始音频信号，但也需要更大的存储空间和传输带宽。

        降低音频的采样率是一种常用的音频压缩方法。通过降低采样率，可以减少每秒钟采样的次数，从而降低音频数据的存储空间和传输带宽要求。

        降低采样率会导致频谱范围的缩小和音质的损失。高频部分的信息可能会丢失或减少，从而影响音频的细节和高音质感。因此，在进行音频压缩时，需要权衡音频的存储空间和音质之间的平衡。

        实际的图像和音频压缩算法通常结合多种技术，包括量化、转换编码、熵编码等，以实现更高效的压缩效果。具体的实现取决于压缩算法的选择和应用的需求。

3.3 基于模型的压缩

        基于模型的压缩是一种有损压缩算法，通过建立对数据的统计模型或预测模型，对数据进行压缩。这种方法利用了数据的统计特性和冗余信息来实现压缩，并且在解压缩时需要使用相同的模型来恢复数据。

3.3.1 视频压缩中的帧间压缩算法

        在视频压缩中，帧间压缩是一种常用的压缩技术。它利用视频帧之间的相关性来减少冗余数据的存储和传输。帧间压缩基于两个关键概念：运动估计和差异编码。

• 运动估计：视频序列中的相邻帧通常具有相似的内容，因为相邻帧之间的目标通常不会发生巨大变化。运动估计算法通过比较相邻帧之间的像素来估计目标的运动矢量。这样可以找到最佳的位移补偿，即在编码帧中仅存储目标移动的差异信息，而不是完整的帧数据。

• 差异编码：通过对目标移动的差异信息进行编码，可以进一步减少数据的存储和传输量。差异编码技术可以分为帧间差分编码和帧内差分编码。

  • 帧间差分编码：在帧间差分编码中，参考帧（关键帧或已编码的帧）与当前帧进行比较，只存储当前帧与参考帧之间的差异信息。这样可以大大减少数据量，因为参考帧通常是周期性的关键帧。

  • 帧内差分编码：在帧内差分编码中，当前帧中的每个像素与其周围像素进行比较，存储像素值之间的差异。这种编码方法适用于当前帧与参考帧之间的差异较小的情况。

3.3.2 实现一个简单的视频压缩程序

        实现一个完整的视频压缩程序需要涉及许多复杂的技术和算法，包括运动估计、差异编码、变换编码、熵编码等。这超出了单个回答的范围。然而，以下是一个简单的视频压缩程序的基本步骤：

1. 视频分解：将视频分解为一系列连续的帧，每帧由像素组成。

2. 运动估计：对于每个帧，使用运动估计算法估计其与参考帧之间的运动矢量。

3. 差异编码：对于每个帧，根据运动估计结果，计算当前帧与参考帧之间的差异信息，并将差异信息编码。

4. 变换编码：对于差异信息，可以使用变换编码技术（如离散余弦变换）将其转换为频域表示。

5. 熵编码：对于变换编码后的数据，使用熵编码算法（如哈夫曼编码）进行进一步的压缩。

6. 压缩数据存储：将压缩后的数据存储为压缩视频文件。

7. 解压缩：使用相同的压缩算法和步骤，对压缩视频文件进行解压缩，以恢复原始的视频数据。

        需要注意的是，上述步骤只是一个简单的示例，实际的视频压缩程序涉及到更多的细节和优化。在实际的视频压缩算法中，还需要考虑编码参数的选择、帧类型的划分、编码延迟等因素，以获得更好的压缩效果和解压缩质。

4. 压缩算法的效果评估与比较

4.1 压缩比率、解压速度和质量损失的衡量指标

        压缩算法的效果可以通过多个指标来评估和比较，其中包括压缩比率、解压速度和质量损失等。这些指标可以帮助我们了解压缩算法的压缩效果、解压缩速度以及数据的还原质量。

1. 压缩比率（Compression Ratio）： 压缩比率是指压缩后的数据大小与原始数据大小之间的比值。它衡量了压缩算法在压缩数据时能够达到的压缩程度。通常以百分比或小数形式表示。较高的压缩比率表示算法可以更有效地减少数据的存储空间。

2. 解压速度（Decompression Speed）： 解压速度是指在解压缩过程中恢复原始数据所需的时间。它衡量了压缩算法在解压缩数据时的效率。通常以单位时间内解压缩的数据量或解压缩一个单位数据所需的时间来表示。较快的解压速度表示算法可以在较短的时间内还原数据。

3. 质量损失（Quality Loss）： 质量损失是指在压缩和解压缩过程中可能引入的数据损失或失真。由于压缩算法通常是有损的，压缩后的数据与原始数据之间可能存在一定的差异。质量损失可以通过与原始数据的比较来评估，例如图像的清晰度、音频的音质等。较小的质量损失表示算法能够在保持较高压缩比率的同时尽量减少数据的失真。

4.2 常见压缩算法的效果比较

以下是一些常见的压缩算法及其效果比较：

1. 无损压缩算法：

   • 哈夫曼编码：具有较高的压缩比率和解压速度，适用于文本数据和较小的数据集。质量无损。
   • LZW算法：具有较高的压缩比率和解压速度，适用于文本和图像数据。质量无损。
   • 预测编码：如算术编码和差分编码，压缩比率较高，但解压速度较慢。质量无损。

2. 有损压缩算法：

   • JPEG压缩算法：适用于图像压缩，具有较高的压缩比率和解压速度，但会引入一定的图像质量损失。
   • MP3压缩算法：适用于音频压缩，具有较高的压缩比率和解压速度，但会引入一定的音质损失。
   • 视频编码算法：如H.264、HEVC等，具有较高的压缩比率和解压速度，但会引入一定的视频质量损失。

        需要注意的是，压缩算法的效果评估和比较取决于具体的应用场景和数据类型。不同的算法可能在不同的数据集上表现出不同的效果，因此选择合适的压缩算法需要考虑数据特征、应用需求以及对压缩比率、解压速度和质量损失的权衡。

5. 压缩算法的应用和发展趋势

5.1 图像、音频和视频压缩的应用场景

        压缩算法在各个领域中被广泛应用，并且不断发展和改进。以下是压缩算法在图像、音频和视频压缩方面的应用场景以及压缩算法的新进展和研究方向：

图像压缩的应用场景:

• 数字图像存储和传输：压缩算法用于减小图像文件的大小，便于存储和传输，如在网页、社交媒体和移动应用中的图片展示。
• 医学图像处理：在医学影像领域，压缩算法可用于减小医学图像的存储空间，并实现高效的传输和处理，如CT扫描、MRI等医学图像的压缩和传输。

音频压缩的应用场景：

• 音乐流媒体：压缩算法用于将音乐文件压缩为较小的大小，以便在互联网上进行流媒体传输，如在线音乐平台和音乐应用程序。
• 语音通信：在语音通信领域，压缩算法用于实现语音通话和语音传输的高效压缩，如VoIP（Voice over Internet Protocol）通信和语音消息传输。

视频压缩的应用场景：

• 视频流媒体：压缩算法用于将视频文件压缩为较小的大小，以便在互联网上进行实时的视频流媒体传输，如在线视频平台和视频会议应用。
• 数字电视和广播：在数字电视和广播领域，压缩算法用于将高清和超高清视频压缩为适合传输和存储的格式，如H.264和HEVC（High Efficiency Video Coding）。

5.2 压缩算法的新进展和研究方向

• 深度学习在压缩算法中的应用：近年来，深度学习技术在压缩算法中的应用逐渐增多，如使用卷积神经网络（CNN）进行图像和视频的无损和有损压缩。
• 新的编码标准和算法：研究人员不断提出新的编码标准和算法，以提高压缩效率和减少质量损失，如AV1视频编码标准的发展和应用。
• 跨媒体压缩：随着多媒体数据的不断增加，跨媒体压缩成为一个新的研究方向，旨在实现多种媒体数据（如图像、音频、视频）的联合压缩和传输。
• 高效的硬件实现：为了满足实时和高性能的应用需求，研究人员致力于开发高效的硬件实现方式，如使用专用硬件加速器和图形处理单元（GPU）来加速压缩和解压缩过程。

        总的来说，压缩算法在图像、音频和视频处理中具有重要的应用价值，并且在不断发展和创新，以适应日益增长的多媒体数据需求和应用场景的要求。

6. 总结

6.1 对压缩算法的综述和总结

        压缩算法是在信息传输和存储中起到重要作用的技术。通过压缩算法，可以将数据的表示形式进行优化，以减少存储空间或传输带宽的需求。压缩算法分为无损压缩算法和有损压缩算法两种类型，每种类型都有其适用的应用场景和特点。

        无损压缩算法保持数据的完整性，不引入信息损失，适用于那些对数据的精确性和准确性要求较高的场景。常见的无损压缩算法包括哈夫曼编码、字典编码、预测编码等。这些算法通过利用数据中的统计特性和重复模式来实现压缩效果。

        有损压缩算法在一定程度上牺牲了数据的精确性，但通过去除冗余信息和利用人类感知的特性，可以大幅度减小数据的大小。常见的有损压缩算法包括转换编码、量化和基于模型的压缩等。这些算法主要应用于图像、音频和视频压缩，能够在保持较高视觉或听觉质量的同时减小文件大小。

6.2 对未来压缩算法发展的展望

未来压缩算法的发展趋势包括以下几个方面：

• 深度学习的应用：深度学习技术在压缩算法中的应用越来越广泛，通过神经网络模型的学习和优化，可以获得更好的压缩效果和质量控制。
• 跨媒体压缩：随着多媒体数据的融合和互通，跨媒体压缩成为一个新的研究方向，旨在实现多种媒体数据的联合压缩和传输。
• 硬件加速：为了满足实时和高性能的应用需求，将会出现更多的硬件加速方案，如专用硬件加速器和图形处理单元（GPU），以提高压缩和解压缩的速度和效率。
• 新的编码标准和算法：研究人员将不断提出新的编码标准和算法，以提高压缩效率、减少质量损失，并满足不断增长的多媒体数据需求。

        综上所述，压缩算法是信息处理中不可或缺的技术之一。通过无损和有损的压缩算法，我们能够有效地减小数据的大小，提高存储和传输效率，并在满足特定需求下保持数据的质量。随着技术的不断进步和应用需求的不断增长，压缩算法将继续发展和创新，为多媒体数据处理和通信领域带来更多的便利和效益。

展望:

未来的压缩算法发展将会面临更多的挑战和机遇。以下是一些展望和研究方向：

• 高效率与高质量的平衡：压缩算法需要在减小数据大小的同时，尽量保持高质量的重建效果。未来的研究将致力于提高压缩效率的同时，降低质量损失，以满足更高要求的应用场景。
• 跨媒体压缩：随着多媒体数据的融合和交互应用的增加，跨媒体压缩将成为一个重要的研究方向。研究人员将致力于实现图像、音频、视频等不同类型数据的联合压缩和传输，以提高整体的压缩效率和效果。
• 深度学习的应用：深度学习技术在压缩算法中的应用将会持续发展。通过神经网络模型的学习和优化，可以获得更好的压缩效果和质量控制。未来将会出现更多基于深度学习的压缩算法和标准。
• 跨平台和移动设备压缩：随着移动设备的普及和移动通信的发展，对于在移动设备上进行实时压缩和传输的需求越来越高。未来的研究将关注于跨平台的压缩算法和针对移动设备的优化，以满足移动应用的需求。
• 新的应用领域：随着科技的不断进步，新的应用领域将涌现出来，对压缩算法提出新的挑战。例如，物联网、虚拟现实和增强现实等领域对数据压缩和传输的需求将变得更加复杂和多样化，需要新的算法和技术的支持。

        总的来说，压缩算法是一个活跃且不断发展的领域，未来将持续有新的算法、标准和技术涌现，以满足不断增长的多媒体数据处理和传输需求。压缩算法的进一步研究和创新将为数据处理、通信和存储等领域带来更大的便利和效益。