论文信息

STFL: A Spatial-Temporal Federated Learning Framework for Graph Neural Networks

原文地址：STFL: A Spatial-Temporal Federated Learning Framework for Graph Neural Networks：https://arxiv.org/abs/2111.06750
源码：https://github.com/JW9MsjwjnpdRLFw/TSFL

摘要

We present a spatial-temporal federated learning framework for graph neural networks, namely STFL. The framework explores the underlying correlation of the input spatial-temporal data and transform it to both node features and adjacency matrix. The federated learning setting in the framework ensures data privacy while achieving a good model generalization. Experiments results on the sleep stage dataset, ISRUC_S3, illustrate the effectiveness of STFL on graph prediction tasks.

我们提出了一个面向图神经网络的时空联邦学习框架STFL。该框架挖掘输入时空数据的底层相关性，并将其转化为节点特征和邻接矩阵。框架中的联邦学习设置在保证数据隐私的同时实现了良好的模型泛化性。在睡眠阶段数据集ISRUC S3上的实验结果说明了STFL在图预测任务上的有效性。

Contributions

1. 我们首先实现了处理时空数据的图生成器，包括特征提取和节点相关性探索；
2. 将图生成器集成到提出的STFL中，设计了一个端到端的时空GNN在图级分类任务上的联邦学习框架；
3. 在真实睡眠数据集ISRUC S3上进行了大量的实验；
4. 在Github1上发布STFL的源代码。

Methodology

STFL框架：

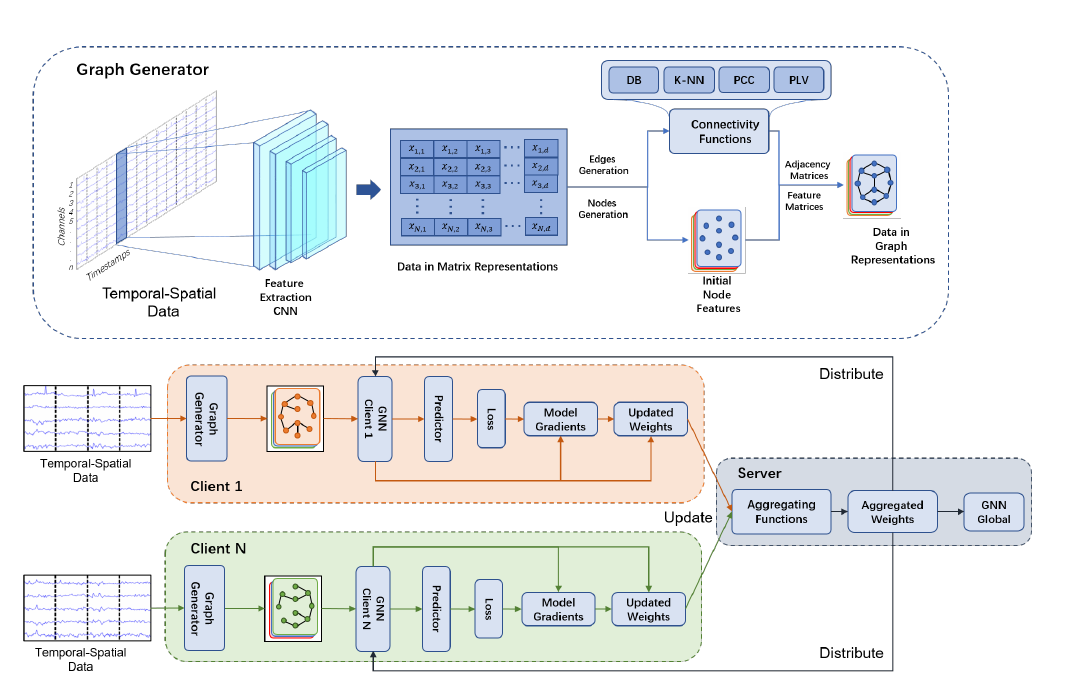
Graph Generation

将时空序列视为原始输入。定义一个多变量序列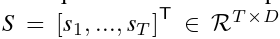定义为时间序列集，其中有总 T 个时间戳，每个时间戳都有 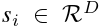维度信号频率。由于时空数据中没有节点概念，因此我们利用空间通道并将其视为节点，这意味着如果有 N 个通道，则转换后的图数据结构中将有 N 个节点。

假设每个通道都有一个时间序列集S，具有完整通道的时空序列表示为 。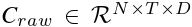
之后，使用基于 CNN 的特征提取网络将原始时空数据转换为特征矩阵表示，特征提取网的输出为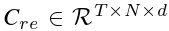，其中d表示特征的维度。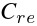的一个快照表示为。
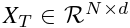获得细化的特征矩阵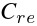后，需要揭示通道（节点）之间的相关性。此时自然会处理 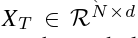节点特征矩阵并检索它们之间的潜在相关性。此后，我们定义了节点相关函数，它将节点特征矩阵作为输入，并输出邻接矩阵：

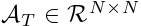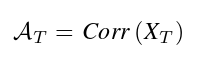
其中Corr（·）在X_T的基础上计算每个通道（节点）的相关性或依赖性。节点相关函数有多种选择，例如皮尔逊相关函数或相位锁定值函数等。

Graph Neural Network

沿着时间维度，我们得到 {G1， …， GT} 作为整个图数据集，表示每个时间戳处生成的图数据，我们使用 {y1， …， yT} 来对应图标签。我们在这里制定了图预测任务，其中图生成器的输出期望被正确预测。为了表示法简单，我们使用 VT 来表示每个 GT 中的节点集，节点 V 的数量与节点特征矩阵 XT 中的行号基本相同。对于每个 v ∈ V，相应的节点特征写为 。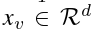

我们使用 ne[v] 来表示节点 v 的邻域，其相关值可以从邻接矩阵 A 中检索。然后，我们制定GNN的消息传递和readout阶段。设 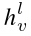表示第l层中的节点嵌入。节点 v 从第 l 层到第 l +1 层的消息传递可以形式化为：
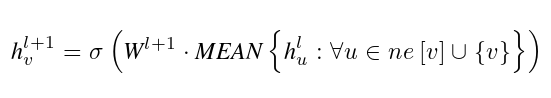其中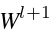，表示第l+1层的可学习变换矩阵，σ表示激活函数。GNN 通过聚合所有邻居表示和自身来更新嵌入 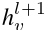的节点。

为了在L层消息传递层后获得整个图的表示，GNN执行readout操作，从节点嵌入中导出最终的图表示，可以表述如下：

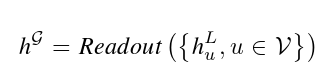
Readout（·）是一种排列不变运算，它可以是简单的均值函数，也可以是更复杂的图形级池化函数，如MLP。
在完全监督设置中，我们使用浅层神经网络来学习图嵌入和label空间Y之间的映射。 σ（·）是一种非线性变换，可以推广为：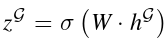
此外，我们利用基于图的二进制交叉熵函数来计算监督设置中的损失L。损失函数公式为：

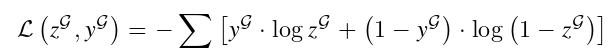
联邦学习

STFL在联邦学习设置下训练来自不同客户的GNN。STFL 包含一个中央服务器 S 和 n 个客户端 C。每个客户端部署一个 GNN，它从本地图形数据中学习客户端，并将 GNN的权重上传到中央服务器。中央服务器接收来自所有客户端的权重，更新全局GNN模型的权重WS，并将更新的权重分发回每个客户端。在这项工作中，我们选择FedAvg作为聚合函数，它平均每个客户端的权重以生成服务器上全局GNN的权重。

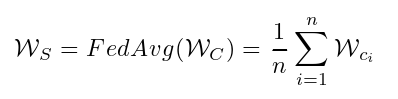
Experiment

数据集

在我们的实验中，ISRUC S3（Khalighi等人，2016）被用作基准数据集。ISRUC S3 从 10 个健康受试者（即睡眠实验参与者）的 10 个通道中收集多导睡眠图 （PSG） 记录。根据 AASM 标准（Jia 等人，2020 年），这些PSG 记录被标记为五个不同的睡眠阶段，包括唤醒、N1、N2、N3 和 REM。如前文部分所述，我们采用基于 CNN 的特征提取网（Jia 等人，2021 年）来生成初始节点特征。为了生成邻接矩阵，分别实现和讨论四种不同的节点关联函数。为了评估STFL的有效性，我们遵循非iiddata设置（Zhang等人，2020年），并将不同的睡眠阶段分配给客户，以验证我们提出的框架的有效性。

Node Correlation Functions

• DB 是欧几里得距离函数，用于测量电极对之间的空间距离。
• K-NN （Jiang et al. 2013） 生成邻接矩阵，该矩阵仅选择每个节点的 k 个最近邻域来表示图的节点相关性。
• PCC（Pearson and Lee 1903）被称为Pearson相关函数，用于测量每对节点之间的相似性。
• PLV（Aydore， Pantazis， and Leahy 2013）是一个随时间变化的节点相关函数，用于测量每对节点的信号。

性能比较分析

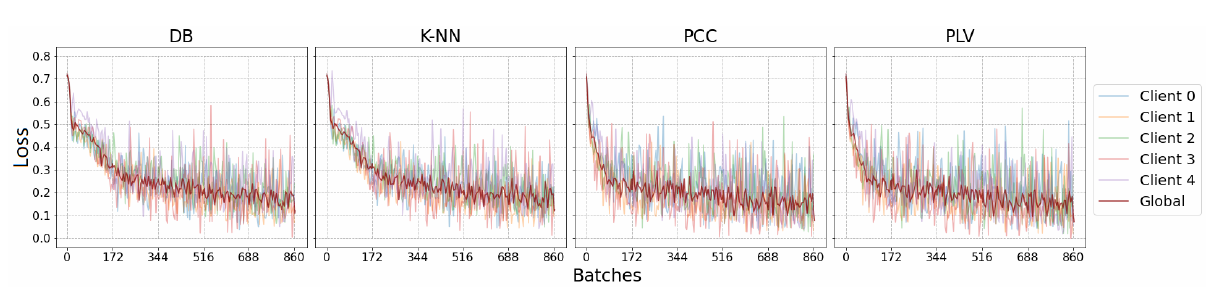
1. 为了评估四个节点相关函数的有效性，我们比较了每个节点相关函数在联邦化设置下对GCN的影响，因为GCN在三个GNN模型中具有最简单的结构。如图 2 所示，PCC 和 PLV 在联合设置下工作良好，收敛速率更快，尤其是在前两个时期。此外，与其他节点相关函数相比，如表2所示，3个联邦模型的PLV的F1得分最高，其次是PCC，DB最差。这可能是由于CNN模型（特征提取网络）中的池化层，该模型着眼于输入序列的小时间窗口，可以使用PLV从中提取每对节点的正确相关性。
   

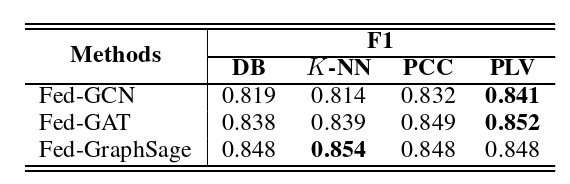
2. 为了评估STFL的有效性，我们从不同的角度测试了它的性能。在我们的实验中，我们首先评估了带有PLV的ISRUC S3上的联邦图模型，因为PLV在RQ1中讨论的四个节点相关函数中每个形式最好。如表3所示，在STFL下，所有三个GNN模型都产生了合理的结果。特别是在联合设置下，GAT在PLV上实现了最高的F1分数和准确性，GraphSage位居第二。
   此外，我们检查了这三个图网络的集中模型的结果，结果也如表3所示。在这一部分中，超参数与联合实验保持不变。对于数据拆分，测试数据与联邦学习实验中的数据相同。训练数据从所有客户端的聚合数据中随机采样，训练数据的大小与一个客户端的大小相同。对于集中设置下的所有GNN，GraphSage获得了最高的F1分数和准确性，其次是GCN。此外，与集中式设置相比，在联合设置下训练的所有模型都获得了更好的结果（F1score和准确性）。这表明在STFL下训练的模型成功地在非IID设置下生成了数据分布。另一个发现是，集中式设置中最好的GNN模型不一定是联邦环境中最好的。

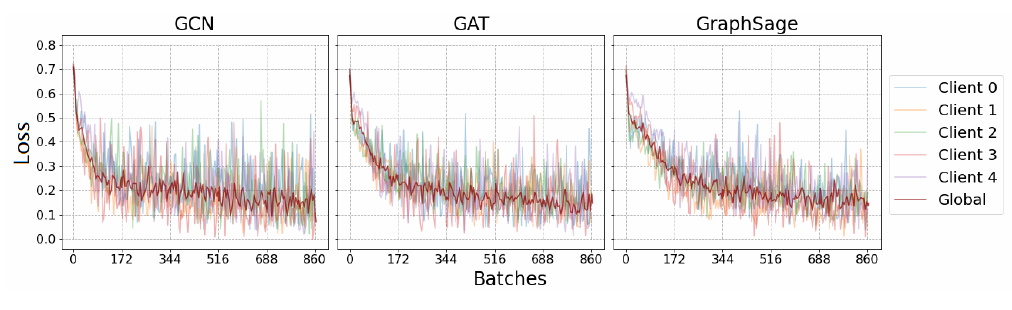
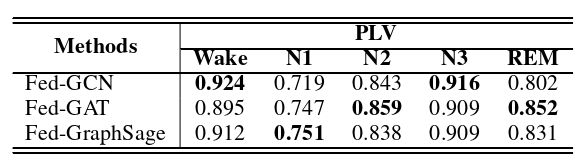
3. 为了确定GNN与STFL的最佳匹配，在联合框架下在ISRUC S3和PLV上测试了三个GNN，因为观察到PLV在所有节点相关函数中获得了最佳结果，其细节在RQ1中进行了分析。如图3所示，GCN收敛速度最快，但比其他两个更不稳定。我们还发现，GraphSage在第一个纪元收敛最慢，但在测试阶段实现了稳定的损失降低。它还发现，所有三个模型最终收敛到相同的损失，在0.15左右波动。此外，我们使用PLV评估每个班级的F1分数。表4显示，对于REM而言，GraphSage表现最好，而GCN在其他四个类别中得分最高。
   有趣的是，三个模型的训练损失在大范围内波动，特别是在最近三个时期。这可能是因为联合框架将全局模型分发给每个训练批次中的每个客户端。在训练的后期阶段，每个客户端都无法在广义全局模型中很好地拟合自己的数据，特别是对于那些容易过度拟合的模型。