您现在的位置是：首页 >技术交流 >C++:二叉搜索树(非平衡化)网站首页技术交流
C++:二叉搜索树(非平衡化)
简介C++:二叉搜索树(非平衡化)
文章目录
一.二叉搜索树(key_value模型)
- 树的节点定义:
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
//key是用于实现搜索功能以及搜索树其他功能的关键值
K _key;
//value用于存储数据
V _value;
//树结点的默认构造函数
BSTreeNode(const K& key = K(), const V& value = V())
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
- 如果一颗二叉树是二叉搜索树,则其具有如下性质:
- 左子树的所有结点的key值都比根结点的key值小
- 右子树的所有结点的key值都比根结点的key值大
- 二叉搜索树的左右子树仍为二叉搜索树
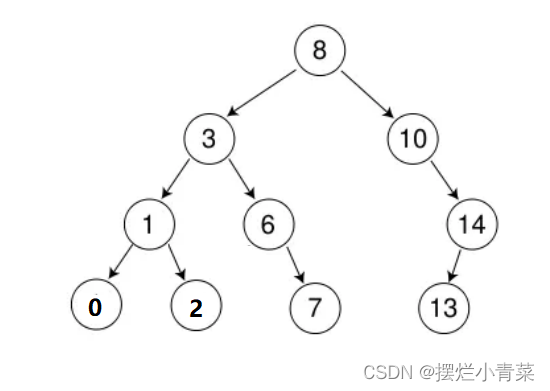
- 二叉搜索树满足递归定义
- 容易证明,二叉搜索树的中序遍历序列是一个升序序列(因此二叉搜索树具有排序功能,也被称作二叉排序树)
- 根据搜索树的定义可知,树中不存在key值相同的节点,因此搜索树还具有去重的功能
- 二叉搜索树C++类模板总览:
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
//供外界调用的功能接口(通过复用内部私有接口实现)
//强制生成类的默认构造函数
BSTree() = default;
//利用前序遍历递归完成拷贝构造
BSTree(const BSTree<K,V>& t)
{
_root = _Copy(t._root);
}
//通过复用拷贝构造实现赋值运算符重载
BSTree<K,V>& operator =(BSTree<K,V>t)
{
std::swap(t._root, _root);
return (*this);
}
//插入节点
bool InsertR(const K& key, const V& value)
{
return _InsertR(_root,key, value);
}
//查找节点
Node* Find(const K& key)
{
return _FindR(_root,key);
}
//删除节点(这里调用递归的接口)
bool Erase(const K& key)
{
return _EraseR(_root, key);
}
//中序遍历搜索树
void InOrder()
{
_InOrder(_root);
}
//搜索树的析构函数
~BSTree()
{
_Destroy(_root);
}
protected:
//私有功能接口
//用于实现拷贝构造的辅助函数(前序递归实现)
Node* _Copy(const Node* root);
//后序遍历销毁二叉树
void _Destroy(Node*& root);
//递归实现插入节点
bool _InsertR(Node*& root, const K& key,const V& value);
//递归实现节点查找
Node * _FindR(Node*& root, const K& key);
//递归删除搜索树结点
bool _EraseR(Node*& root, const K& key);
//非递归删除搜索树结点
bool _Erase(Node *&root,const K& key)；
//中序遍历搜索树
void _InOrder(Node* root);
//寻找子树key值最大的结点的接口
Node* _FindMax(Node* root);
private:
//根节点指针
Node* _root = nullptr;
};
二.二叉搜索树的节点删除
- 搜索树节点删除操作必须保持二叉搜索树的结构性质不变
- 非递归删除搜索树节点
-
接口首部:
bool _Erase(Node*& root, const K& key)(删除成功则返回true,否则返回false) -
代码逻辑思维导图:
-
删除情况1演示:
-
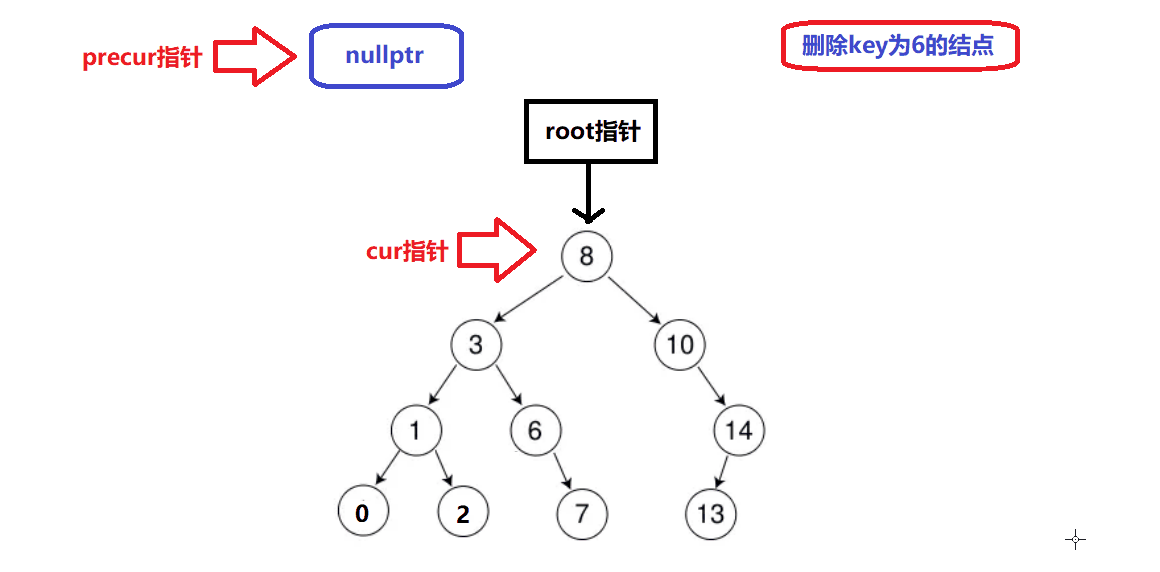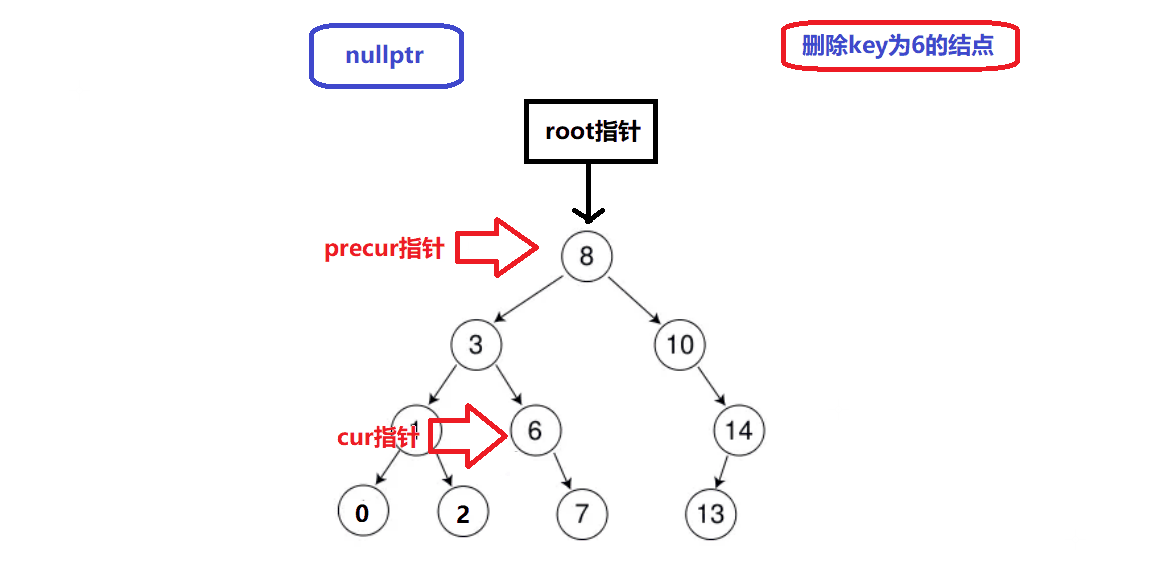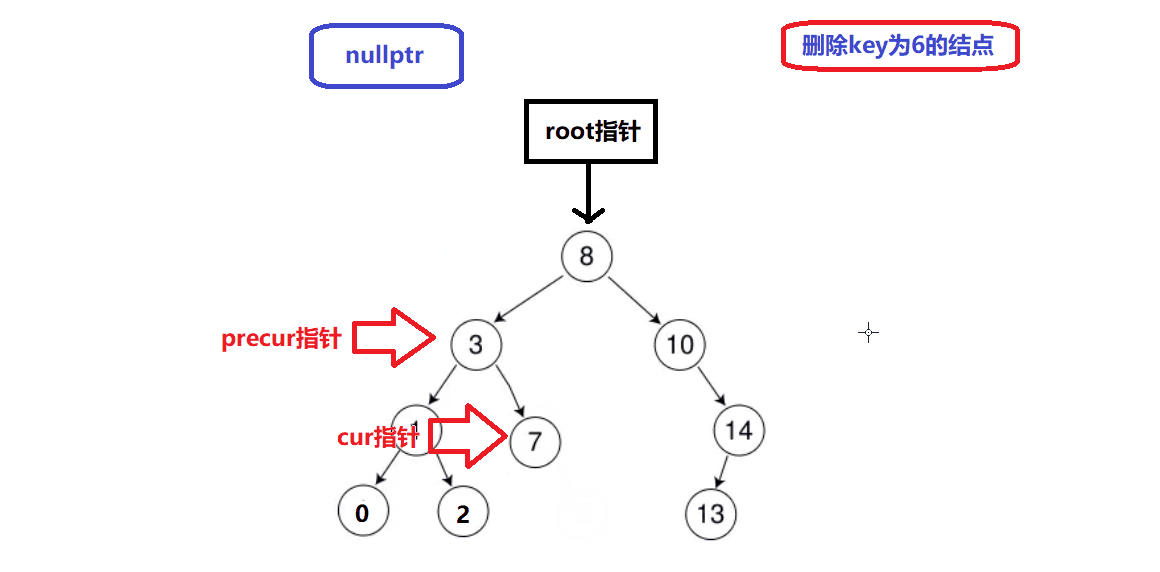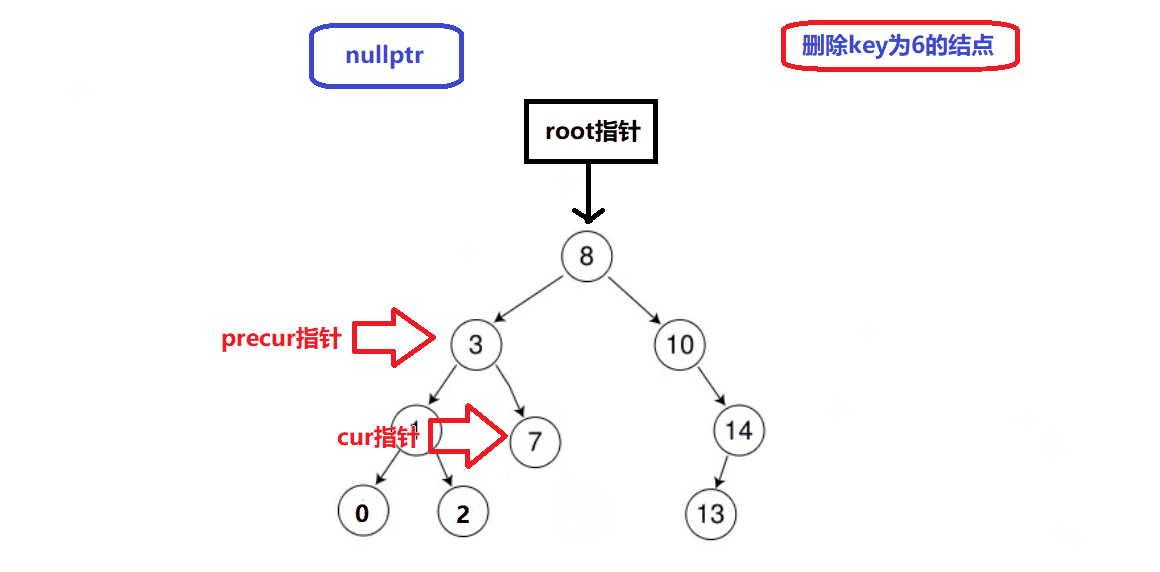
删除情况3演示:
-
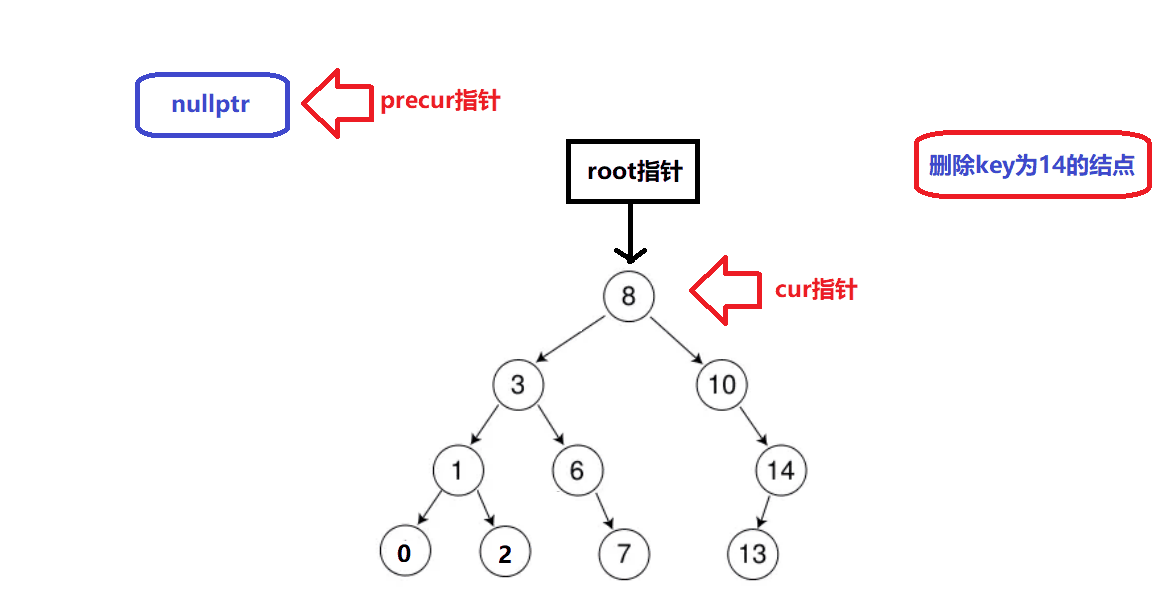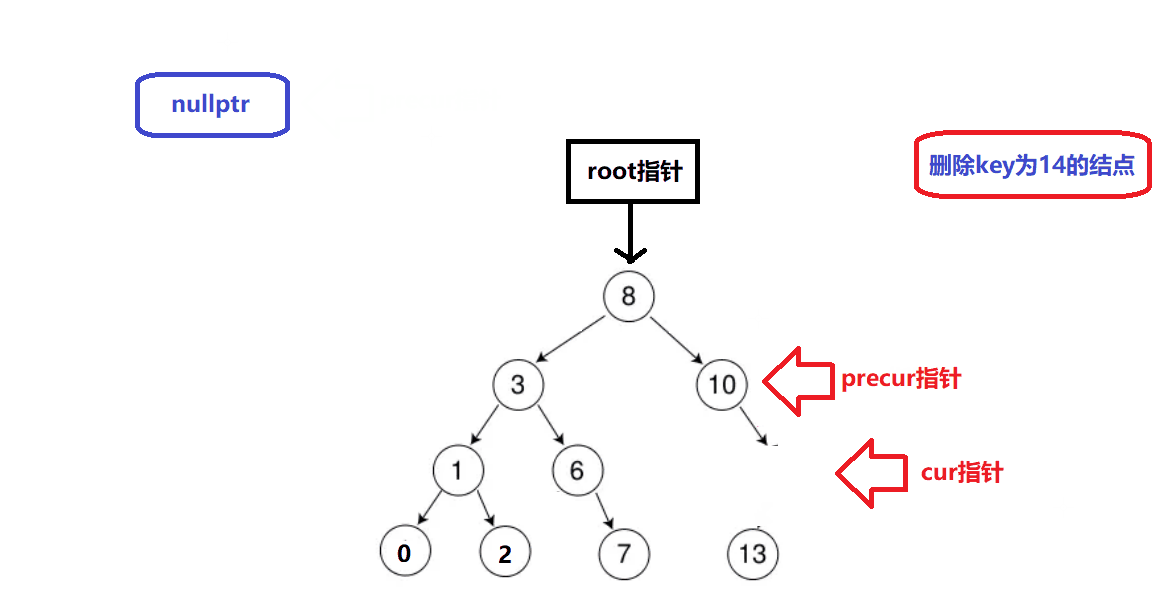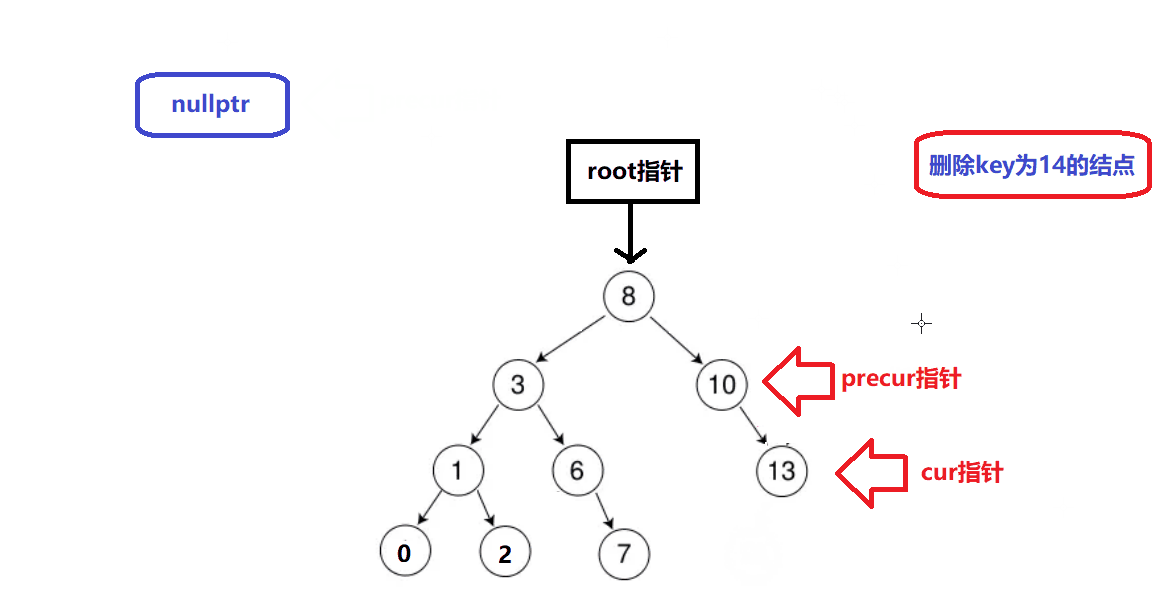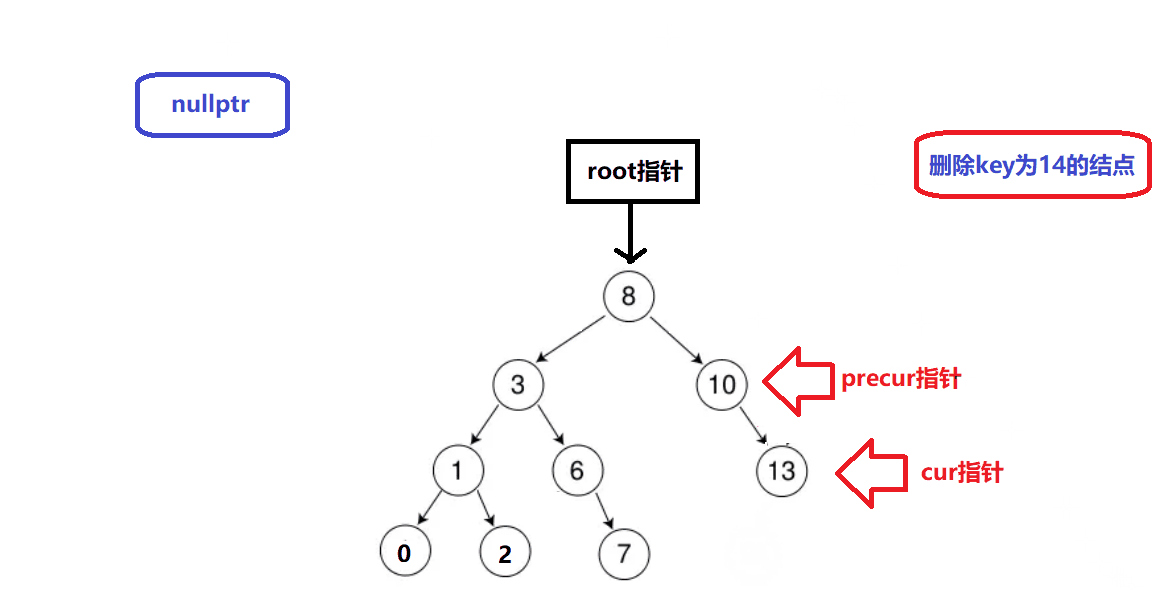
删除情况2演示:
-
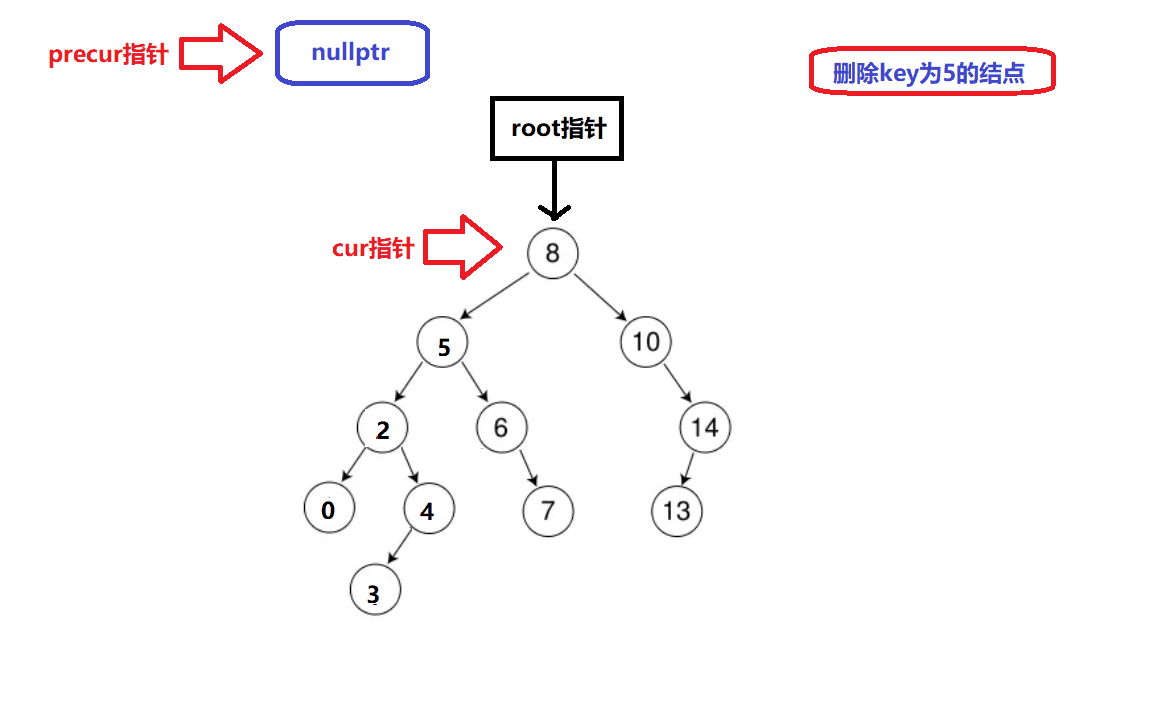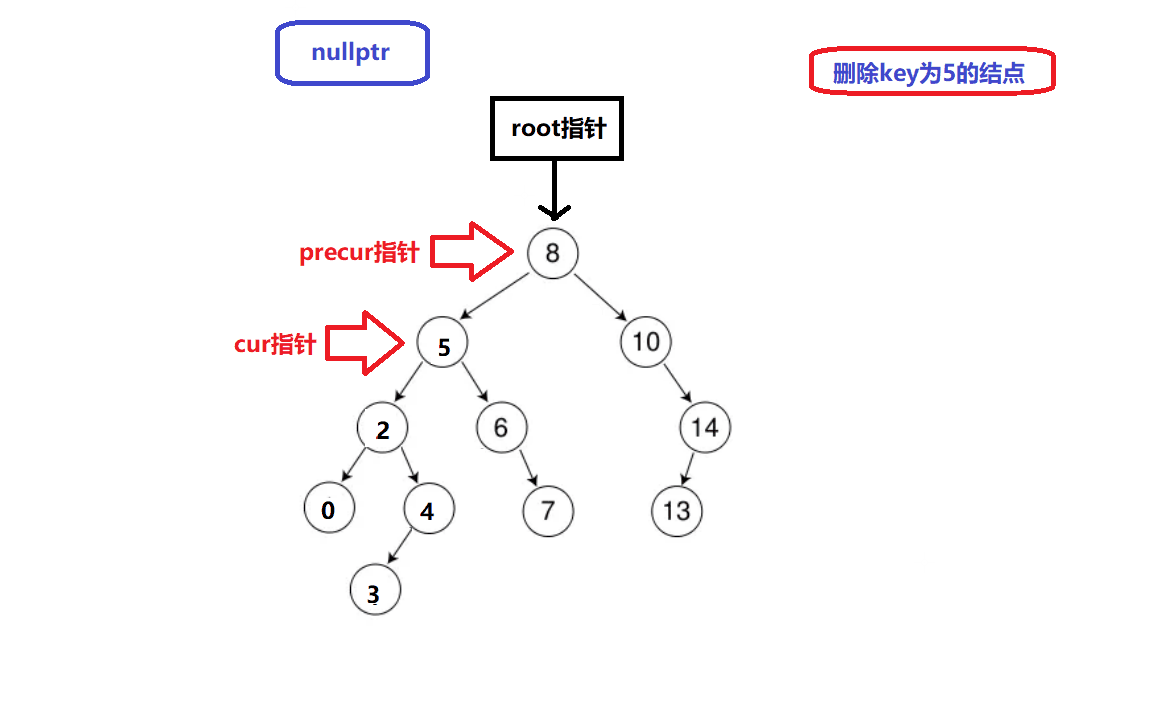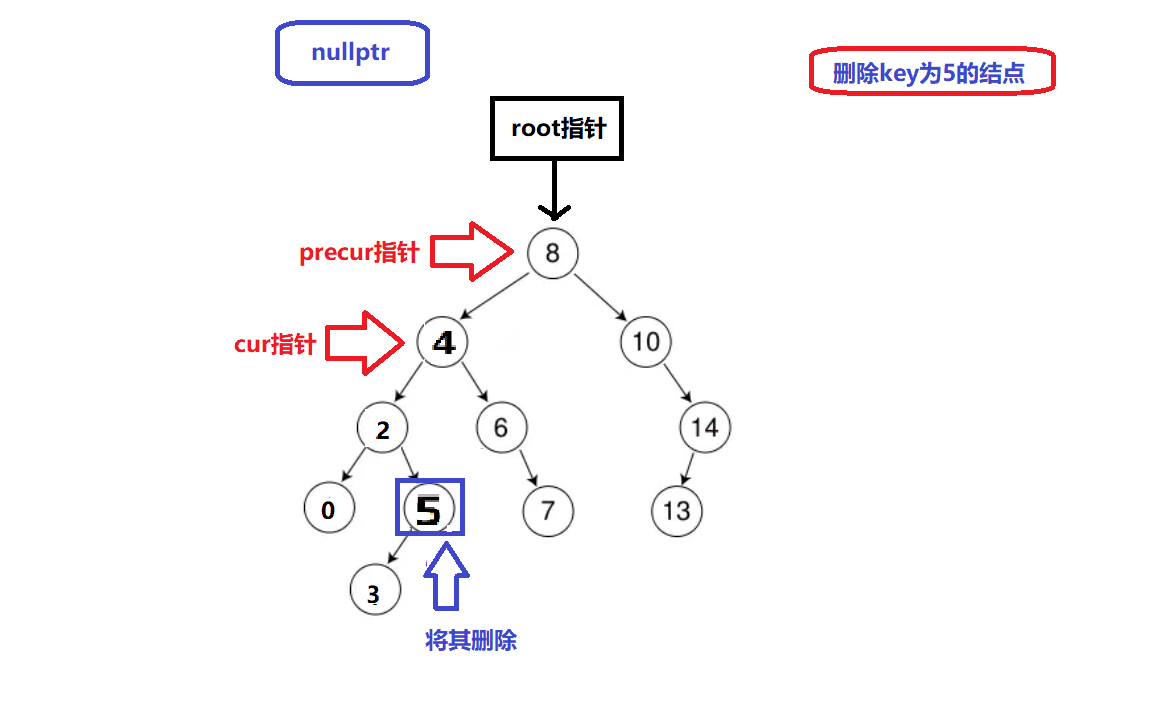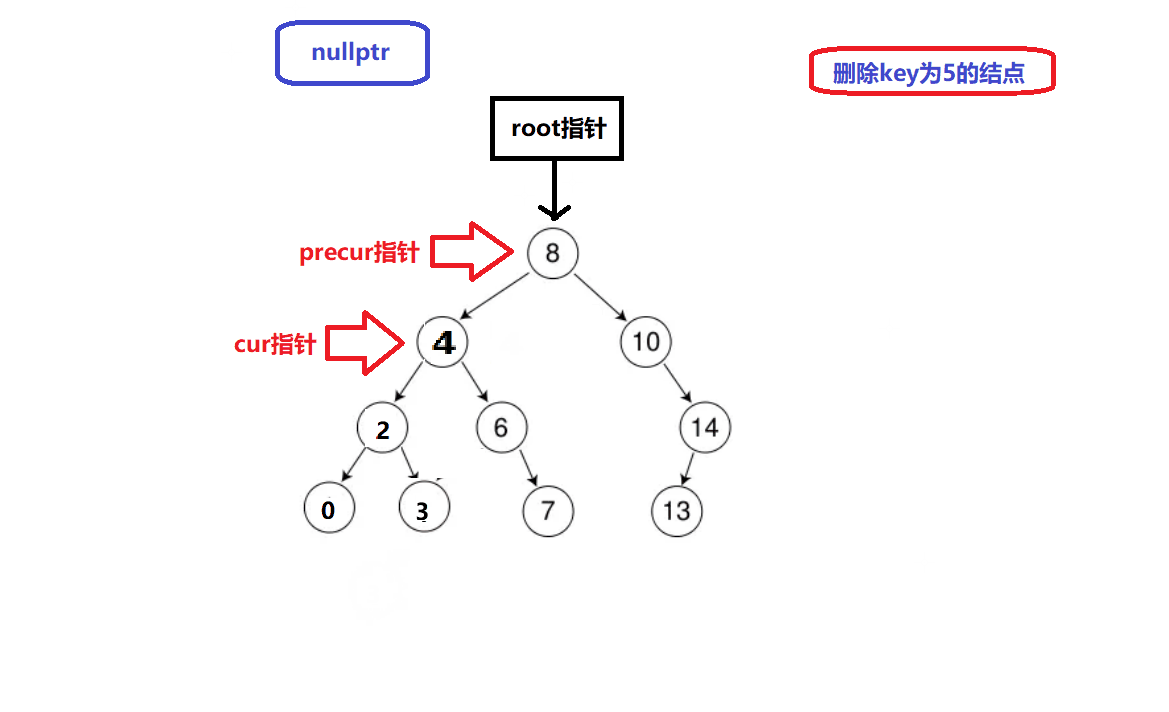
情况2中的子树最值替换删除法保证了搜索树的结构性质以及删除方式的简洁性和逻辑唯一性
-
非递归删除结点代码:
-
//非递归删除节点
bool _Erase(Node*& root, const K& key)
{
Node* precur = nullptr;
Node* cur = root;
while (cur)
{
if (cur->_key > key)
{
precur = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
precur = cur;
cur = cur->_right;
}
else
{
//执行删除操作
//找到待删除节点
//待删除结点只可能有右孩子
if (cur->_left == nullptr)
{
//判断待删结点是否为根节点
if (root == cur)
{
root = cur->_right;
}
else
{
//将右孩子交给前驱指针
if (precur->_left == cur)
{
precur->_left = cur->_right;
}
else
{
precur->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
return true;
}
//待删除结点只有左孩子
else if (cur->_right == nullptr)
{
//判断待删结点是否为根节点
if (root == cur)
{
root = cur->_left;
}
else
{
//将左孩子交给前驱指针
if (precur->_left == cur)
{
precur->_left = cur->_left;
}
else
{
precur->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
return true;
}
//待删除结点既有左孩子又有右孩子
else
{
//用左子树的最大结点与待删节点进行替换后,再删除待删节点
Node* Maxpre = cur;
Node* Max = cur->_left;
while (Max->_right)
{
Maxpre = Max;
Max = Max->_right;
}
std::swap(Max->_key, cur->_key);
//将左孩子交给前驱指针
if (Maxpre->_left == Max)
{
Maxpre->_left = Max->_left;
}
else
{
Maxpre->_right = Max->_left;
}
delete Max;
Max = nullptr;
return true;
}
}
}
return false;
}
- 递归删除搜索树节点:
- 接口首部
bool _EraseR(Node*& root, const K& key) - 递归删除搜索树节点算法采用节点指针变量的引用进行传参递归,形参直接引用了当前待操作节点的前驱指针,因此在函数中可以直接通过形参对待删除节点的前驱指针进行修改,代码书写上会简单很多
- 递归删除搜索树节点代码:
- 接口首部
//寻找子树最大结点的接口
Node* _FindMax(Node*root)
{
while (root->_right)
{
root = root->_right;
}
return root;
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
else if (root->_key > key)
{
//在左子树中删除节点
_EraseR(root->_left, key);
}
else if (root->_key < key)
{
//在右子树中删除节点
_EraseR(root->_right, key);
}
else
{
Node* del = root;
//对待删除节点进行分类讨论,同样分三类进行讨论
if (root->_left == nullptr)
{
//将右子树交给前驱指针
root = root->_right;
}
else if (root->_right == nullptr)
{
//将左子树交给前驱指针
root = root->_left;
}
else
{
Node* Max = _FindMax(root->_left);
std::swap(Max->_key, root->_key);
//递归删除换位后的目标节点
_EraseR(root->_left, key);
return true;
}
delete del;
return true;
}
}
三.二叉搜索树类对象其他接口
构造函数,析构函数和赋值运算符重载
- 辅助接口
Node* _Copy(const Node* root) - 拷贝构造函数
BSTree(const BSTree<K,V>& t)
//强制编译器生成类的默认构造函数
BSTree() = default;
//用于实现拷贝构造的辅助函数(前序递归实现树的深拷贝)
Node* _Copy(const Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* Root = new Node(root->_key,root->_value);
Root->_left = _Copy(root->_left);
Root->_right = _Copy(root->_right);
return Root;
}
BSTree(const BSTree<K,V>& t)
{
_root = _Copy(t._root);
}
- 赋值运算符重载:
- 接口首部:
BSTree<K,V>& operator =(BSTree<K,V>t),通过复用拷贝构造实现
- 接口首部:
//通过复用拷贝构造实现赋值运算符重载
BSTree<K,V>& operator =(BSTree<K,V>t)
{
std::swap(t._root, _root);
return (*this);
}
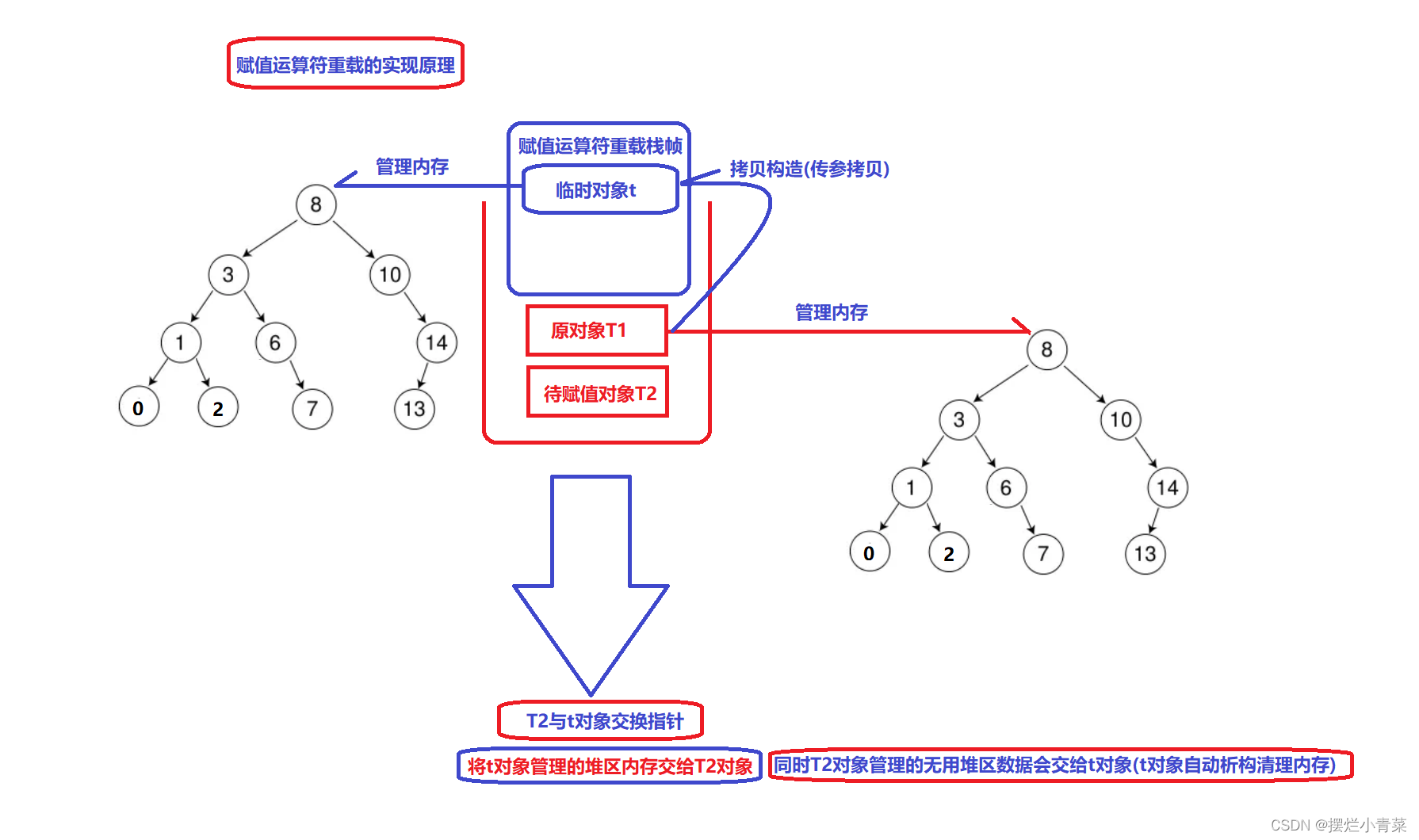
- 析构函数:
- 后序遍历递归释放所有节点
- 辅助接口:
void _Destroy(Node*& root);
//后序遍历销毁二叉树
void _Destroy(Node*& root)
{
if (root == nullptr)
{
return;
}
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
root = nullptr;
}
//搜索树的析构函数
~BSTree()
{
_Destroy(_root);
}
节点插入接口和节点查找接口
- 节点插入接口
- 辅助接口
bool _InsertR(Node*& root, const K& key,const V& value);,通过递归实现节点的插入 - 供外界调用的接口:
bool InsertR(const K& key, const V& value);
- 辅助接口
//递归插入节点
bool _InsertR(Node*& root, const K& key,const V& value)
{
if (root == nullptr)
{
//找到空位置则插入
root = new Node(key,value);
return true;
}
else if (root->_key > key)
{
return _InsertR(root->_left, key,value);
}
else if (root->_key < key)
{
return _InsertR(root->_right, key,value);
}
else
{
//找到相同节点则插入失败
//插入操作中体现了搜索树的去重功能
return false;
}
}
//插入节点
bool InsertR(const K& key, const V& value)
{
return _InsertR(_root, key, value);
}
- 节点查找接口
- 递归实现:
//递归实现查找
Node * _FindR(Node*& root, const K& key)
{
if (root == nullptr)
{
//找到空则说明结点不存在
return nullptr;
}
else if (root->_key > key)
{
return _FindR(root->_left,key);
}
else if (root->_key < key)
{
return _FindR(root->_right,key);
}
else
{
return root;
}
}
//查找节点
Node* Find(const K& key)
{
return _FindR(_root, key);
}
key_value模型二叉搜索树类模板总体代码
namespace key_value
{
#pragma once
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key = K(), const V& value = V())
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
//强制生成类的默认构造函数
BSTree() = default;
//利用前序遍历递归完成拷贝构造
BSTree(const BSTree<K,V>& t)
{
_root = _Copy(t._root);
}
//通过复用拷贝构造实现赋值运算符重载
BSTree<K,V>& operator =(BSTree<K,V>t)
{
std::swap(t._root, _root);
return (*this);
}
//插入节点
bool InsertR(const K& key, const V& value)
{
return _InsertR(_root, key, value);
}
//查找节点
Node* Find(const K& key)
{
return _FindR(_root, key);
}
//删除节点
bool Erase(const K& key)
{
return _EraseR(_root, key);
}
//中序遍历搜索树
void InOrder()
{
_InOrder(_root);
}
//搜索树的析构函数
~BSTree()
{
_Destroy(_root);
}
protected:
//用于实现拷贝构造的辅助函数(前序递归实现树的深拷贝)
Node* _Copy(const Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* Root = new Node(root->_key,root->_value);
Root->_left = _Copy(root->_left);
Root->_right = _Copy(root->_right);
return Root;
}
//后序遍历销毁二叉树
void _Destroy(Node*& root)
{
if (root == nullptr)
{
return;
}
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
root = nullptr;
}
//递归插入节点
bool _InsertR(Node*& root, const K& key,const V& value)
{
if (root == nullptr)
{
//找到空位置则插入
root = new Node(key,value);
return true;
}
else if (root->_key > key)
{
return _InsertR(root->_left, key,value);
}
else if (root->_key < key)
{
return _InsertR(root->_right, key,value);
}
else
{
//找到相同节点则插入失败
return false;
}
}
//递归实现查找
Node * _FindR(Node*& root, const K& key)
{
if (root == nullptr)
{
//找到空则说明结点不存在
return nullptr;
}
else if (root->_key > key)
{
return _FindR(root->_left,key);
}
else if (root->_key < key)
{
return _FindR(root->_right,key);
}
else
{
return root;
}
}
//非递归删除节点
bool _Erase(Node*& root, const K& key)
{
Node* precur = nullptr;
Node* cur = root;
while (cur)
{
if (cur->_key > key)
{
precur = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
precur = cur;
cur = cur->_right;
}
else
{
//执行删除操作
//找到待删除节点
//待删除结点只可能有右孩子
if (cur->_left == nullptr)
{
//判断待删结点是否为头节点
if (root == cur)
{
root = cur->_right;
}
else
{
if (precur->_left == cur)
{
precur->_left = cur->_right;
}
else
{
precur->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
return true;
}
//待删除结点只有左孩子
else if (cur->_right == nullptr)
{
//判断待删结点是否为头节点
if (root == cur)
{
root = cur->_left;
}
else
{
if (precur->_left == cur)
{
precur->_left = cur->_left;
}
else
{
precur->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
return true;
}
//待删除结点既有左孩子又有右孩子
else
{
//用左子树的最大结点与待删节点进行替换后,再删除待删节点
Node* Maxpre = cur;
Node* Max = cur->_left;
while (Max->_right)
{
Maxpre = Max;
Max = Max->_right;
}
std::swap(Max->_key, cur->_key);
if (Maxpre->_left == Max)
{
Maxpre->_left = Max->_left;
}
else
{
Maxpre->_right = Max->_left;
}
delete Max;
Max = nullptr;
return true;
}
}
}
return false;
}
//递归删除搜索树结点
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
else if (root->_key > key)
{
_EraseR(root->_left, key);
}
else if (root->_key < key)
{
_EraseR(root->_right, key);
}
else
{
Node* del = root;
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* Max = _FindMax(root->_left);
std::swap(Max->_key, root->_key);
_EraseR(root->_left, key);
return true;
}
delete del;
return true;
}
}
//中序遍历搜索树
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << "结点的key值:" << root->_key << ' ' << "节点的value:" << root->_value << endl;
_InOrder(root->_right);
}
//寻找子树最大结点的接口
Node* _FindMax(Node* root)
{
while (root->_right)
{
root = root->_right;
}
return root;
}
private:
Node* _root = nullptr;
};
}
四.未经平衡化的二叉搜索树的缺陷
- 二叉搜索树的节点插入,删除,查找操作的时间复杂度取决于搜索树的高度
- 在相同节点数量下,完全二叉树的高度是最小的,搜索树为完全二叉树时,节点插入,删除,查找操作的时间复杂度都为O(logN)
- 然而,相同的结点集合,构造出的二叉搜索树高度是不确定的(有时甚至会直接构造出单链表的线性形状,此时搜索树便退化为线性表),比如:
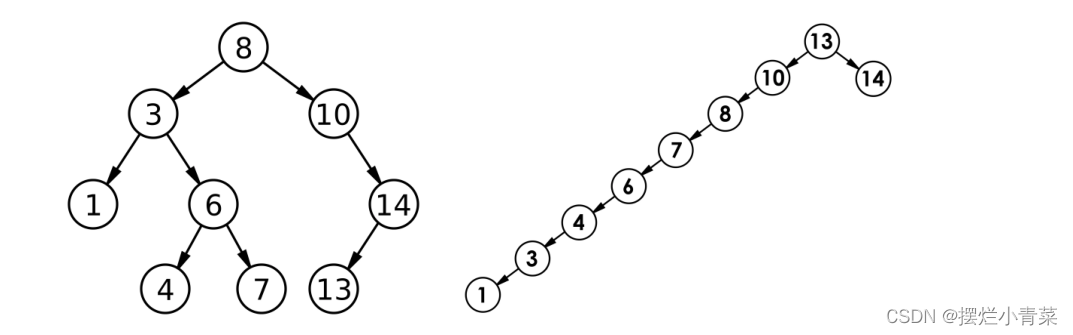
- 因此,想让二叉搜索树在实际场景中发挥作用,就需要平衡化算法对其进行优化(所谓平衡化就是改变搜索树的结构使其接近完全二叉树)
风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。
站长推荐
- stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述
【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述