目录

一、C语言中大致的类型介绍

二、整型家族

三、浮点型家族

一、C语言中大致的类型介绍

我们大致可以将C语言中的类型分为：

（1）整型家族（2）浮点型家族（3）构造类型，也是自定义类型（4）指针类型、（5）空类型

 今天我们重点研究的就是整型家族和浮点型家族在内存中是如何存储的。

二、整型家族

首先来介绍整型家族在内存中的存储：

每个整型家族的成员都可以分成有符号的，和无符号的

在整型家族中一般来说，如果不特别写出他是unsigned 无符号型的，默认他就是有符号类型的；例如：

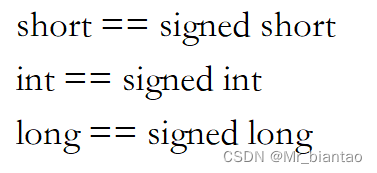
 但是char型就比较特殊了，单独写一个char，他到底是signed char，还是unsigned char，我们不确定，是由我们所用的编译器来决定的。

有符号的和无符号的区别就是：有符号的在存储的二进制位中，他们的第一位表示他们的符号位，是不作为数值位来存储的。无符号则是全部都是数值位。

我们拿char型来做例子   char占4个字节空间，1个字节等于8个比特位。

此时变量ch的二进制展开式的第一位就表示符号位，符号位如果为0就是正数，如果为1就为负数

 剩下的7位则表示的是数值位，0000110转化成十进制就是6

正数的原码、反码、补码相同，我们知道在内存中存的是数据的补码，所以最后在内存中存的就是00000110

我们再来讨论一下整型家族在内存中的所有储存情况：

首先是有符号数：

无符号数：

 所以可以知道：

有符号char的取值范围：-128~127；无符号char的取值范围：0~255

我们可以在limits.h这个头文件中找到所有整型家族的取值范围。浮点型家族的取值范围可以在float.h这个头文件中找到

此时我们发现了一个规律，不管是无符号数还是有符号数都是一个轮回

三、浮点型家族

浮点数其实就是带有小数位的数，就可以称为浮点数

比如123.45；可以表示成12.345 * 10^1；也可以表示成1.2345 * 10^2;

小数点可以来回浮动，所以就称他们位为浮点数。

我们根据国际标准IEEE（电气和电子工程协会）754的规定可以知道。

任意一个二进制浮点数V可以表示成以下形式：

我们可以举一个例子：

我们现在知道了浮点数怎么用科学计数法表示了，就可以来讨论一下浮点型家族在内存中的存储了

由上面我们可以知道，如果知道了一个浮点数的S、M、E那么我们就可以还原出他原本的那个数，所以说，我们在内存里面，只需要存放S、M、E这三个的值就行了。那具体是怎么存的呢？

IEEE 754规定了：

对于一个32位的浮点数（float）最高的1位存放的是S，紧接着的8位存放的是指数E，剩下的23位则为有效数字M

 对于一个64位的浮点数（double）最高的1位存放的是S，紧接着的11位存放的是指数E，剩下的52位则为有效数字M

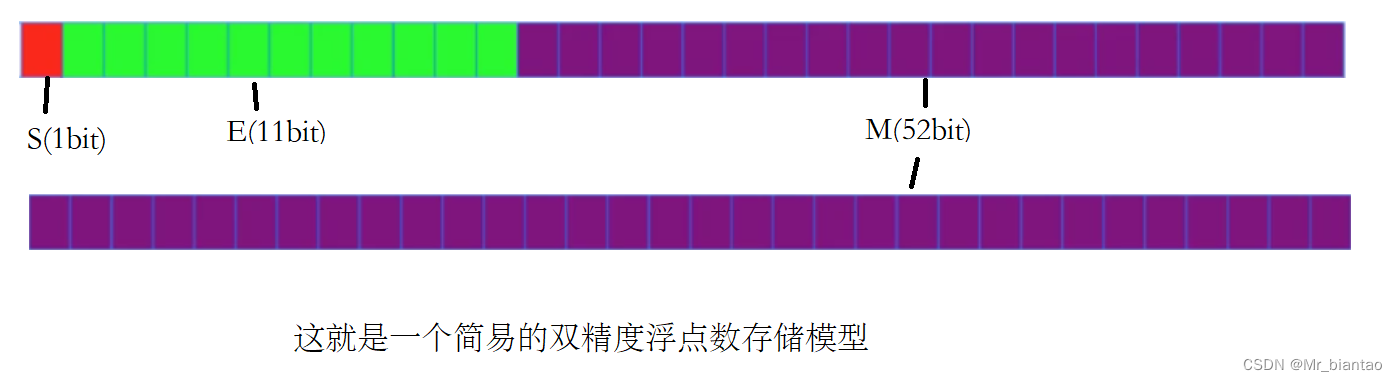
 我们现在知道了 浮点数的S、E、M、在内存中是怎么储存的了。

但是IEEE 754对有效数字M和指数E有特别的规定。

先是对有效数字M的规定：

我们前面了解了M是一个大于1小于二的数，所以常表示成：1.xxxxxxxx的形式，xxxxxx表示的是小数部分。我们发现第一位总会是1，所以IEEE 754规定，在计算机内部保存M的时候，这个1可以被舍去，只保存后面的小数部分，等到需要读取时，在把1加上去，这样就可以节省一个空间来存储更多的有效数字。

比如保存1.0101的时候，我们在内存中只存储后面的0101，会把开头的1省略掉。

再来就是对指数E的规定：

首先对于这个E，他是一个无符号的整数（unsigned int ）

这就代表着，如果是一个32位的浮点数，E为8位，它的取值范围就是0~255；

如果是一个64位的浮点数，E为11位，它的取值范围就为0~2047；

可是在科学计数法中，E是可以出现负数的，所以IEEE 754规定了，E在存入内存时，存的是E的真实值加上一个中间数，这个中间数对于8位的E来说是127，对于11位的E来说是1023

比如：2^3，E是3，如果他是一个32位的浮点数时，在内存中保存的就是3+127=130；

也就是10000010，这些是对于E存入内存中的规定

对于E从内存取出来的规定，又分成了3种情况：

（1）E不是全部为0，或者E不是全部为1的情况：

如果处于这种情况的时候，浮点数在内存中就是这样表示的；

E从内存中取出来时，直接减去127（或1023），得到E的真实值后，再将有效数字M加上小数点前的1。例子：

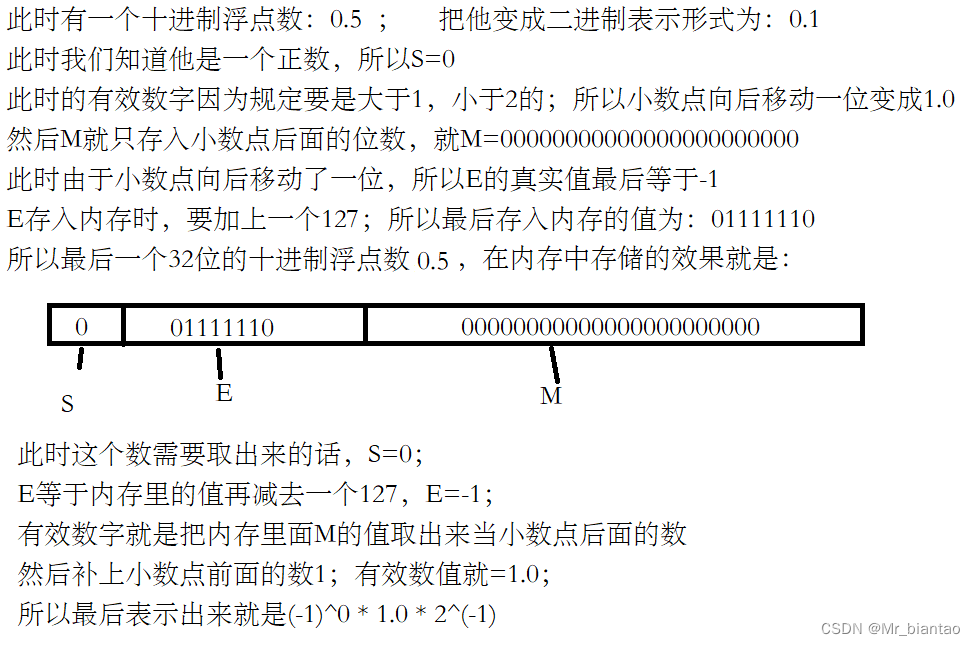
（2）E全部为0的情况：

如果E全为0的情况下，我们可以推出来E的真实值是-127；

那么这个数就变成(-1)^S * 1.xxxx * 2^(-127)算出来的话，会是一个非常小的数值，无限接近于0的数值；

所以此时我们就不用0-127来表示E的真实值了，直接用1-127（或1-1023）来表示E的真实值。

有效数字M取出来的时候也不再加上小数点前面的1了，而是直接还原成0.xxxx这样的数，无限趋近于0的一个数

（3）E全部为1的情况：

如果E全为1的情况下，此时的有效数字M如果全为0，则直接表示±无穷大（具体正负取决于我们的S，为0就为正，为1就为负）

今天给大家的分享就到这里，如果觉得对你们有帮助的话，请给博主一个三连！！！！

你们的三连就是博主更新的动力！！！

谢谢大家！！！！