您现在的位置是：首页 >技术教程 >【数据结构】二叉树（二）网站首页技术教程
【数据结构】二叉树（二）
目录
一、二叉树链式结构及实现
1、二叉树的结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;二叉树链式结构类型，这种是节点类型，包括了左右孩子节点，和该节点的数据值。
2、二叉树的遍历
学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉 树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。下面给出了4中遍历方法。
2.1 前序遍历
先是访问根节点，然后访问左子树，最后访问右子树。
//二叉树前序遍历
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}2.2 中序遍历
先是访问左子树，然后访问根节点，最后访问右子树。
//二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}2.3 后序遍历
先是访问左子树，然后访问右子树，最后访问根节点。
//二叉树后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}2.4 层序遍历
层序遍历，就是按照二叉树每一层的节点进行访问。
思路：需要创建一个队列，首先将根节点放入队列，然后当队列不为空时，就出队头节点，如果队头节点的左子树不为空，它的左子树节点就入队列，如果队头节点的右子树不为空，它的右子树节点就入队列，依次循环，直到队列里面没有节点，此时，层序遍历结束。
//二叉树层序遍历
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d ", front->data);
QueuePop(&q);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
printf("
");
QueueDestroy(&q);
}3、二叉树链式结构的实现
3.1 创建一个节点
要想实现二叉树链式结构，首先要创建节点，创建完节点将其初始化。
//创建一个节点
BTNode* BuyBTNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
exit(-1);
}
node->data = x;
node->left = node->right = NULL;
return node;
}3.2 二叉树节点个数
此处给了两种方法，第一种就是通过全局变量，每到一个结点总数就++。第二种方法就是简化了一下，左子树节点个数+右子树节点个数+根节点。
//二叉树节点个数
int size = 0;
int TreeSize1(BTNode* root)
{
if (root == NULL)
return 0;
//前序遍历
size++;
TreeSize1(root->left);
TreeSize1(root->right);
return size;
}
//二叉树节点个数
int TreeSize2(BTNode* root)
{
return root == NULL ? 0 : TreeSize2(root->left) + TreeSize2(root->right) + 1;
}3.3 二叉树叶子节点个数
计算叶子节点个数，需要分情况讨论，如果根节点为空时，就等于0，如果根节点的左右子树都为空时，叶子节点个数就为1，剩下就是根节点的左右子树都不为空的情况了，此时遍历左子树和右子树计算叶子节点个数。
//二叉树叶子节点个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}3.4 二叉树的高度
二叉树的高度就是算左右两边子树的最大高度。需要递归到最后一层，然后再+当前节点高度。
//二叉树的高度或深度(后序遍历)
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}3.5 二叉树第k层节点个数
同样需要递归根节点的左右子树，看看每一层左右子树有多少个节点，然后相加即可。
//二叉树第k层的节点个数 k >= 1
int TreeKLevelSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
//k > 1 子树的k-1
return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1);
}3.6 二叉树查找值为x的节点
二叉树查找节点的方法也是用的递归，首先先判断这颗二叉树是否为空，如果为空，就不存在x，如果根节点处的值等于x，就找到了，如果没有，就向下进行，先遍历左子树，再遍历右子树，直到找到x。
//二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* ret1 = TreeFind(root->left, x);
if (ret1)
return ret1;
BTNode* ret2 = TreeFind(root->right, x);
if (ret2)
return ret2;
return NULL;
}3.7 判断二叉树是否是完全二叉树
思路：和上面层序遍历一致，同样要是用队列，还是一层一层的将节点入队列，出队列，当出队列遇到空节点时，停止入队列。然后判断队列中是否都是空节点，若都是空节点，则为完全二叉树，否则不为完全二叉树。
//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
else
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
//出到空以后，如果后面全是空，则是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}二、二叉树基础oj练习题
1、单值二叉树
1.1 题目说明
题目链接：单值二叉树
如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。只有给定的树是单值二叉树时，才返回 true；否则返回 false。
1.2 题目解析
思路：如果树为空，则说明是单值二叉树，如果它的左子树不为空且左子树的节点值和根节点值不相等，则返回false，如果它的右子树不为空且右子树的节点值和根节点值不相等，则返回false。
bool isUnivalTree(struct TreeNode* root){
if(root == NULL)
return true;
if(root->left && root->left->val != root->val)
return false;
if(root->right && root->right->val != root->val)
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
}2、检查两棵树是否相同
2.1 题目说明
题目链接：相同的树
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。
2.2 题目解析
思路：判断根，左子树、右子树是否相同——1.判断结构是否相同 2.判断val是否相同。
首先有两种特殊情况，就是如果根节点 p 和 根节点 q 都为空，说明这两棵树为相同的树，如果根节点 p 和 根节点 q ，有一个为空，说明这两棵树不相同。
如果 节点 p 的值不等于节点 q 的值，很明显这两棵树不相同，最后遍历 p 和 q 的左右子树。
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}3、对称二叉树
3.1 题目说明
题目链接：对称二叉树
给你一个二叉树的根节点 root ， 检查它是否轴对称。
3.2 题目解析
思路：为了方便判断这棵树是否是轴对称，我们先写一个函数，判断其轴对称。
轴对称函数其实和上面判断两棵树是否相同一样，就是在最后递归的时候，需要 root1 的左子树和root2 的右子树进行判断是否是相同的，或者是 root1 的右子树和 root2 的左子树进行判断是否是相同的，如果相同，则说明是对称二叉树。
bool _isSymmetric(struct TreeNode* root1,struct TreeNode* root2)
{
if(root1 == NULL && root2 == NULL)
return true;
if(root1 == NULL || root2 == NULL)
return false;
if(root1->val != root2->val)
return false;
return _isSymmetric(root1->left,root2->right) && _isSymmetric(root1->right,root2->left);
}
bool isSymmetric(struct TreeNode* root){
return !root || _isSymmetric(root->left,root->right);
}4、二叉树的前序遍历
4.1 题目说明
题目链接：二叉树的前序遍历
给你二叉树的根节点 root ，返回它节点值的 前序 遍历。
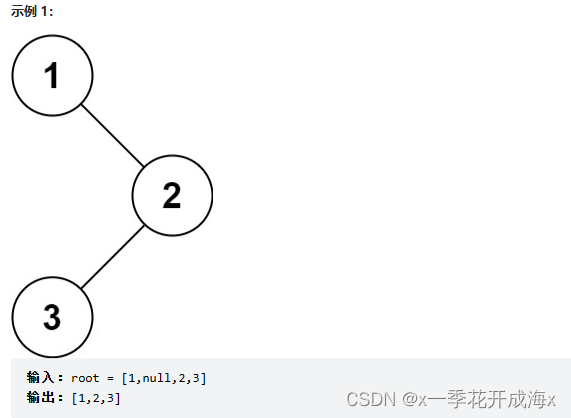
4.2 题目解析
思路1：这种方法是递归形式，先是编写一个前序遍历的算法，前序遍历的访问顺序是根节点，然后是左子树，最后是右子树。
class Solution {
public:
void preorde(TreeNode* root,vector<int>& ret)
{
if(root == nullptr)
return;
ret.push_back(root->val);
preorde(root->left,ret);
preorde(root->right,ret);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ret;
preorde(root,ret);
return ret;
}
};思路2：这种方法是非递归形式，这种思路是将一棵树分为了两部分：(1)左路节点；(2)左路节点的右子树。这里面用到的栈，它的作用就是为了访问左路节点的右子树。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> s;
vector<int> v;
TreeNode* cur = root;
while(cur || !s.empty())
{
while(cur)
{
v.push_back(cur->val);
s.push(cur);
cur = cur->left;
}
TreeNode* top = s.top();
s.pop();
cur = top->right;
}
return v;
}
};5、二叉树的中序遍历
5.1 题目说明
题目链接：二叉树的中序遍历
给你二叉树的根节点 root ，返回它节点值的 中序 遍历。
5.2 题目解析
思路1：用递归方式，先是编写一个中序遍历的算法，中序遍历的访问顺序是左子树，然后是根节点，最后是右子树。
class Solution {
public:
void inorder(TreeNode* root, vector<int>& ret) {
if (root == NULL)
return;
inorder(root->left, ret);
ret.push_back(root->val);
inorder(root->right, ret);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
inorder(root, ret);
return ret;
}
};
思路2： 用的是非递归方式，将一颗二叉树分为两个部分：(1)左路节点；(2)左路节点的右子树。和上面前序遍历的非递归方式一样，不同的是进入 v 的顺序不同。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> s;
vector<int> v;
TreeNode* cur = root;
while(cur || !s.empty())
{
while(cur)
{
s.push(cur);
cur=cur->left;
}
TreeNode* top = s.top();
s.pop();
v.push_back(top->val);
cur = top->right;
}
return v;
}
};6、二叉树的后序遍历
6.1 题目说明
题目链接：二叉树的后序遍历
给你二叉树的根节点 root ，返回它节点值的 后序 遍历。
6.2 题目解析
思路1：用递归方式，先是编写一个后序遍历的算法，后序遍历的访问顺序是左子树，然后是右子树，最后是根节点。
class Solution {
public:
void postorder(TreeNode *root, vector<int> &ret)
{
if (root == nullptr)
{
return;
}
postorder(root->left, ret);
postorder(root->right, ret);
ret.push_back(root->val);
}
vector<int> postorderTraversal(TreeNode *root) {
vector<int> ret;
postorder(root, ret);
return ret;
}
};
思路2：用非递归方式，将一颗二叉树分为两个部分：(1)左路节点；(2)左路节点的右子树。注意：假设第一次取到6时，上一个访问的节点是左子树的根4，第二次取到6时，上一个访问的节点是右子树的根7。所以有了另一个限制条件 top->right == prev 。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> s;
vector<int> v;
TreeNode* cur = root;
TreeNode* prev = nullptr;
while(cur || !s.empty())
{
while(cur)
{
s.push(cur);
cur = cur->left;
}
TreeNode* top = s.top();
//1.右为空 或者 右子树已经访问过了(上一个访问的节点是右子树的根)，可以访问根节点
if(top->right == nullptr || top->right == prev)
{
v.push_back(top->val);
s.pop();
prev = top;
}
else
{
//访问左路节点右子树 ---- 子问题
cur = top->right;
}
}
return v;
}
};7、另一颗树的子树
7.1 题目说明
题目链接：另一棵树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
7.2 题目解析
思路：三步走：1.判断它们是不是相同的树 2.判断subRoot是不是root的左子树 3.判断subRoot是不是root的右子树。
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
if (p == NULL && q == NULL)
return true;
//其中一个为空
if (p == NULL || q == NULL)
return false;
if (p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root == NULL)
return false;
if(isSameTree(root,subRoot))
return true;
return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}
本文要是有不足的地方，欢迎大家在下面评论，我会在第一时间更正。
老铁们，记着点赞加关注!!!
站长推荐
- stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述
【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述