您现在的位置是：首页 >其他 >【数据结构】二叉树的链式结构（笔记总结）内附递归展开图（炒鸡详细）网站首页其他
【数据结构】二叉树的链式结构（笔记总结）内附递归展开图（炒鸡详细）
简介【数据结构】二叉树的链式结构（笔记总结）内附递归展开图（炒鸡详细）
👦个人主页：@Weraphael
✍🏻作者简介：目前学习C++和算法
✈️专栏：数据结构
🐋 希望大家多多支持，咱一起进步！😁
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注✨
前言
上期学习了二叉树堆的存储结构，但它只适合表示完全二叉树，非完全二叉树则会浪费空间。而链式结构恰恰能解决这个问题
目录
一、什么是链式存储
顾名思义就是用链表来表示一颗二叉树。 通常的方法是：链表中每个结点由三个域组成，数据域、左指针域和右指针分别用来给出该结点存储的数据、左孩子和右孩子所在的链结点的存储地址 。
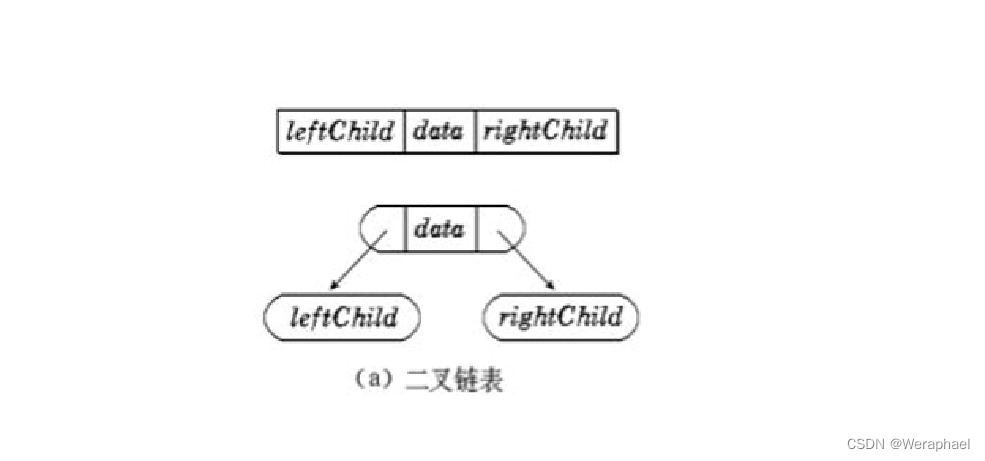
二、链式二叉树的结构
typedef int BTreeData;
typedef struct BinaryTree
{
BTreeData data; //当前节点值域
struct BinartTree* left; //指向当前节点左孩子
struct BinartTree* right;//指向当前节点右孩子
}BT;
三、链式二叉树的实现
3.1 二叉树的遍历
- 学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
- 二叉树的四种遍历
- 前序遍历（前根遍历）：遍历顺序为
根 左子树 右子树- 中序遍历（中根遍历）：遍历顺序为
左子树 根 右子树- 后序遍历（后根遍历）：遍历顺序为
左子树 右子树 根
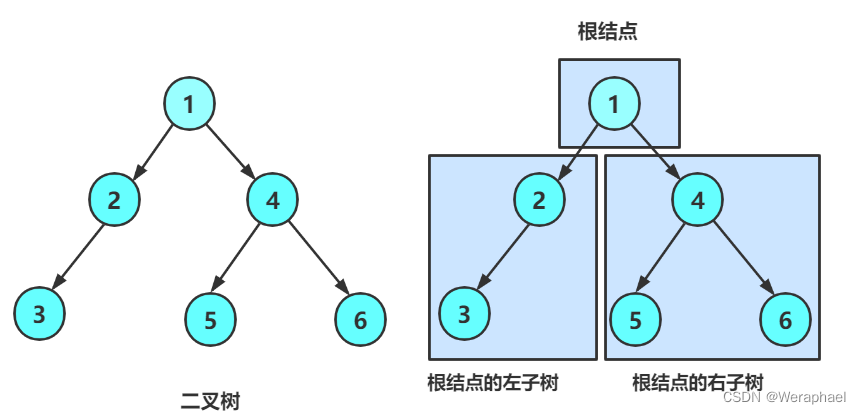
再实现二叉树遍历之前，回顾一下二叉树的概念，二叉树是：
- 空树
- 非空：根节点，根节点的左子树、根节点的右子树组成的
从概念中可以看出，二叉树定义是递归式的，因此后序操作中基本都是按照递归实现的。
BT* BuyTreeNode(BTreeData x)
{
BT* newnode = (BT*)malloc(sizeof(BT));
if (newnode == NULL)
{
perror("newnode :: malloc");
return NULL;
}
newnode->data = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
BT* CreateTree()
{
BT* node1 = BuyTreeNode(1);
BT* node2 = BuyTreeNode(2);
BT* node3 = BuyTreeNode(3);
BT* node4 = BuyTreeNode(4);
BT* node5 = BuyTreeNode(5);
BT* node6 = BuyTreeNode(6);
node1->left = node2;
node2->left = node3;
node1->right = node4;
node4->left = node5;
node4->right = node6;
return node1;
}
int main()
{
BT* root = CreateTree();
return 0;
}
在学习二叉树的基本操作前，首先需要创建一棵二叉树。由于目前知识有限，我们不能直接写出二叉树真的创建，因此现在我们可以手搓一颗二叉树。而这棵树的原型以上图为例。
3.11 前序遍历
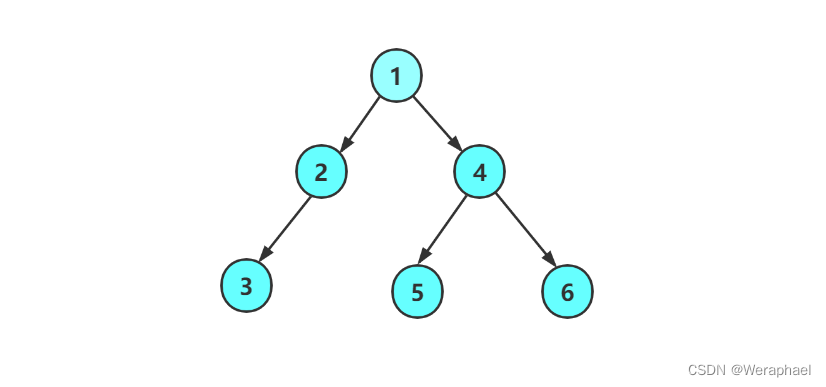
以上图为例，它的前序遍历是怎么样的呢？
根 左子树 右子树
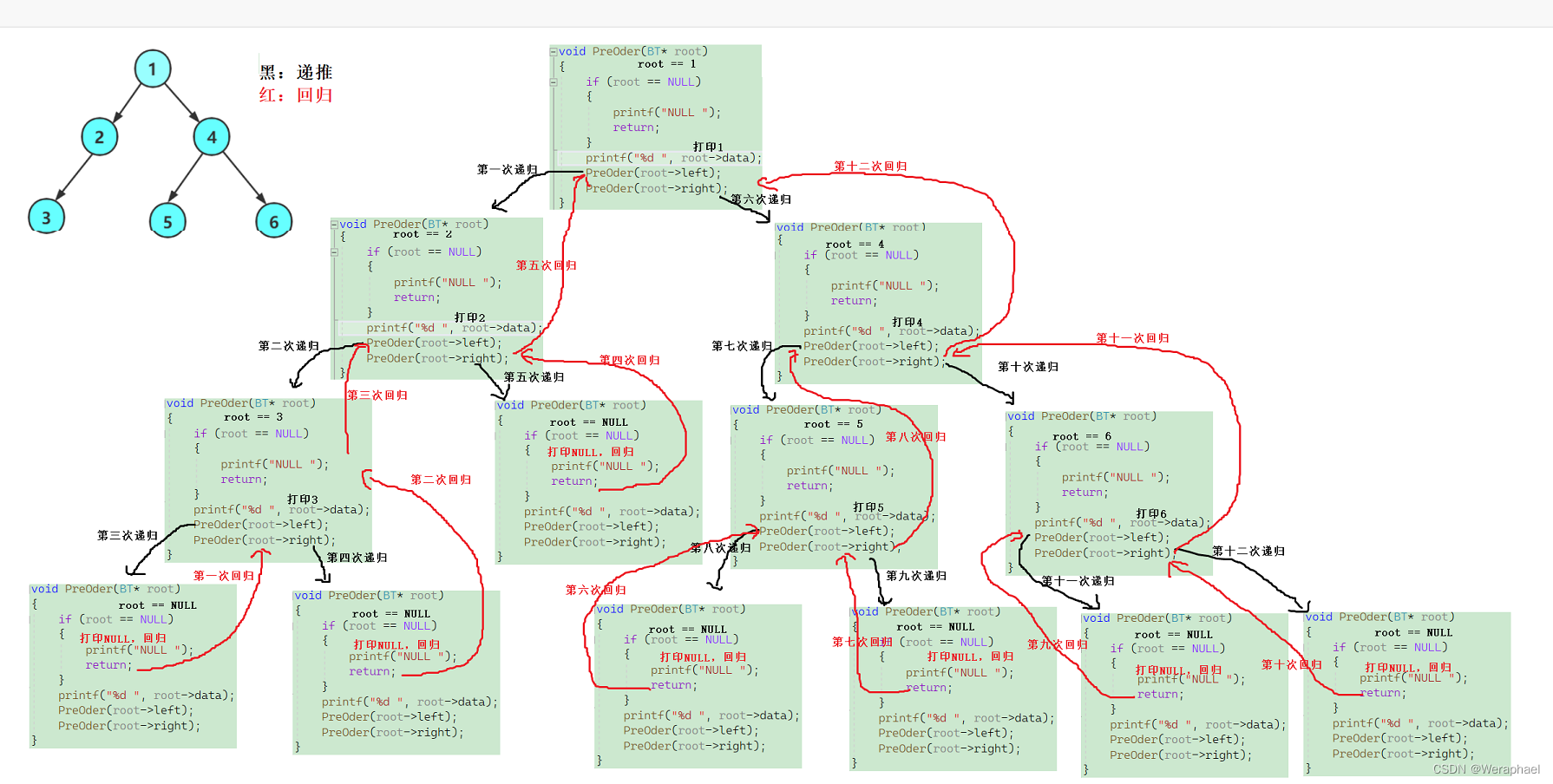
- ①作为树的根，因此第一个先打印1，接下来访问①的左子树②
- ②又可以作为根，因此第二个再打印2，接下来访问②的左子树③
- ③又可以作为根，因此第三个再打印3，接下来访问③的左子树NULL
- ③的左树NULL已经不能再当做根了(因为是空树)，为了体现过程，我们可以把第四个NULL打印出来
- 接下来访问③的右子树NULL，同上，打印第五个打印NULL
- 接下来③这颗树又作为②的左树，因此接下来访问②的右树NULL，第六个打印NULL
- 接下来②这课树又作为①的左树，因此接下来访问①的右树④，而④又可以作为根，因此第七个打印4
- 接下来访问④的左树⑤，⑤又能作为根，因此第八个打印5
- 接下来访问⑤的左树NULL，第九个打印NULL
- 接下来访问⑤的右树NULL，第十个打印NULL
- 然后⑤又作为④的左树，因此接下来访问④的右树⑥，⑥又作为根，因此第十一个打印6
- 接下来访问6的左子树NULL，第十二个打印NULL
- 然后再访问⑥的右子树NULL，第十三个打印NULL
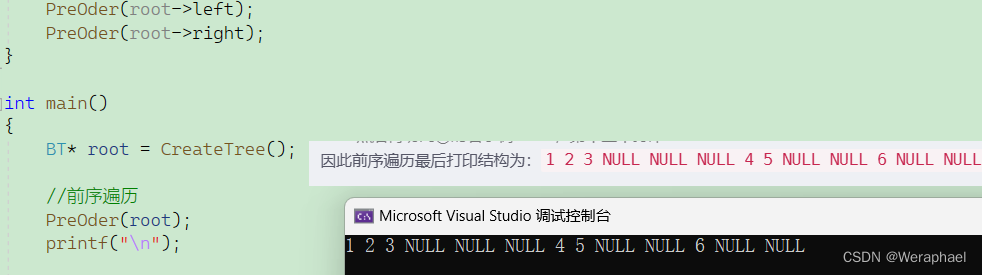
综上，前序遍历最后打印顺序为：
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
【代码实现】
void PreOder(BT* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
//先访问根
printf("%d ", root->data);
//左子树
PreOder(root->left);
PreOder(root->right);
}
int main()
{
BT* root = CreateTree();
//前序遍历
PreOder(root);
printf("
");
return 0;
}
【结果展示】
【递归展开图】
3.12 中序遍历
以上图为例，它的中序遍历是怎么样的呢？
左子树 根 右子树
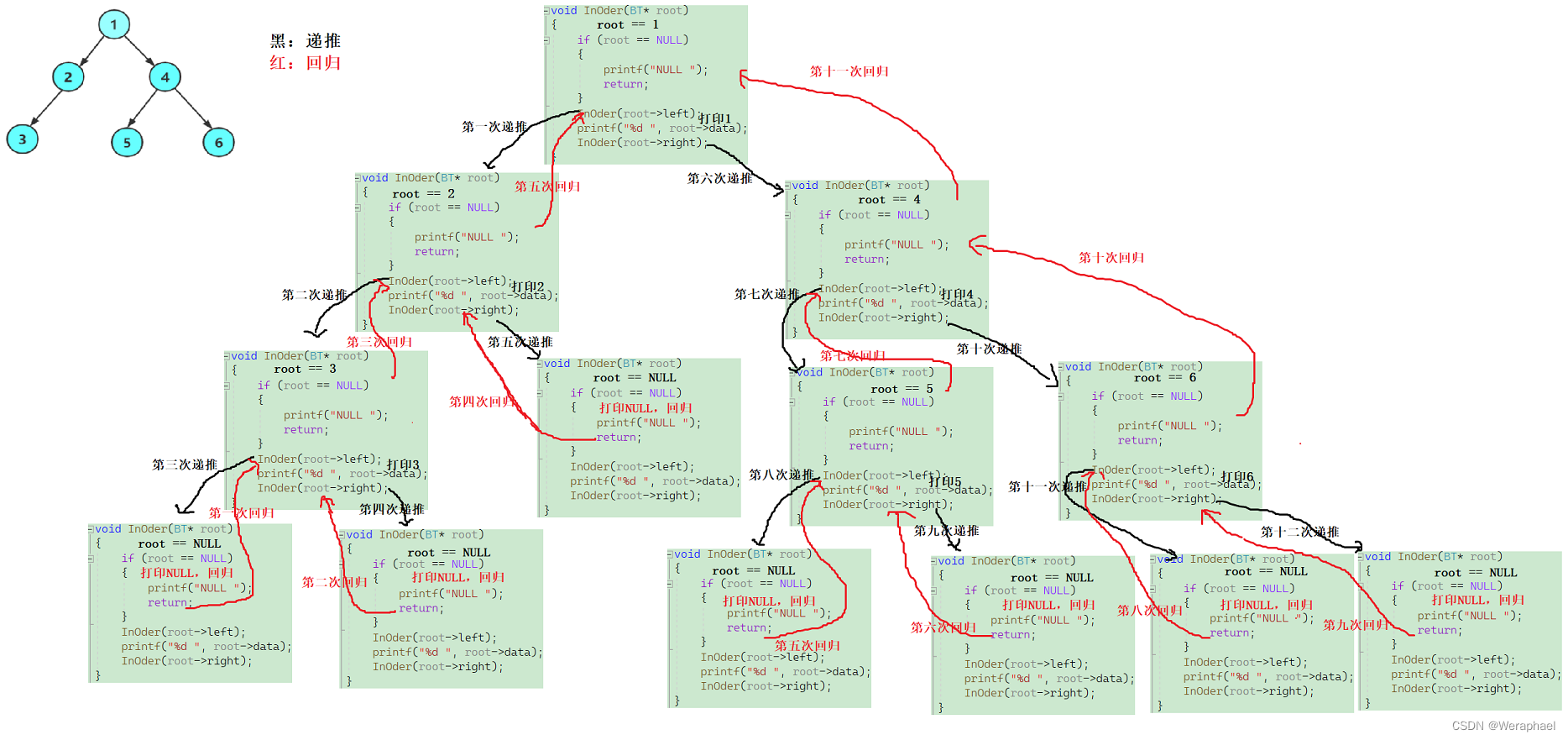
- 根据中序遍历的访问顺序，在遍历的过程中，由于①、②、③都属于根节点，因此第一次打印的结点是③的左子树NULL，其次打印根3，最后再打印③的右子树NULL
- 然后，③又作为②的左子树，因此接下来打印根2，再打印②的右子树NULL
- 接下来，②又作为①的左子树，因此接下来打印根1，再打印①的右子树，但是注意，不能直接打印④，因为④可以作为根。因此接下来要先打印根⑤的左子树NULL，再打印根5，最后再打印⑤的右子树NULL
- 最后，⑤又作为④的左子树，所以接下来要打印根4，再访问④的右子树，但是不能直接访问⑥，因为⑥也能作为根。因此先打印⑥的左子树NULL，再打印根6，最后打印⑥的右子树NULL
综上，中序遍历的顺序为：
NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
【代码实现】
//中序遍历
void InOder(BT* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOder(root->left);
printf("%d ", root->data);
InOder(root->right);
}
int main()
{
BT* root = CreateTree();
//中序遍历
InOder(root);
printf("
");
return 0;
}
【结果展示】
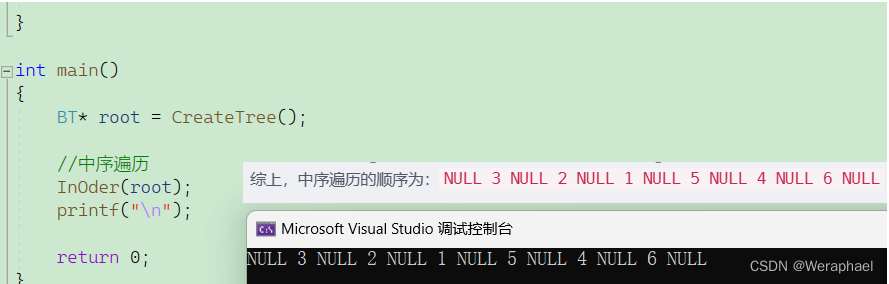
【递归展开图】
3.13 后序遍历
以上图为例，它的后序遍历是怎么样的呢？
左子树 右子树 根
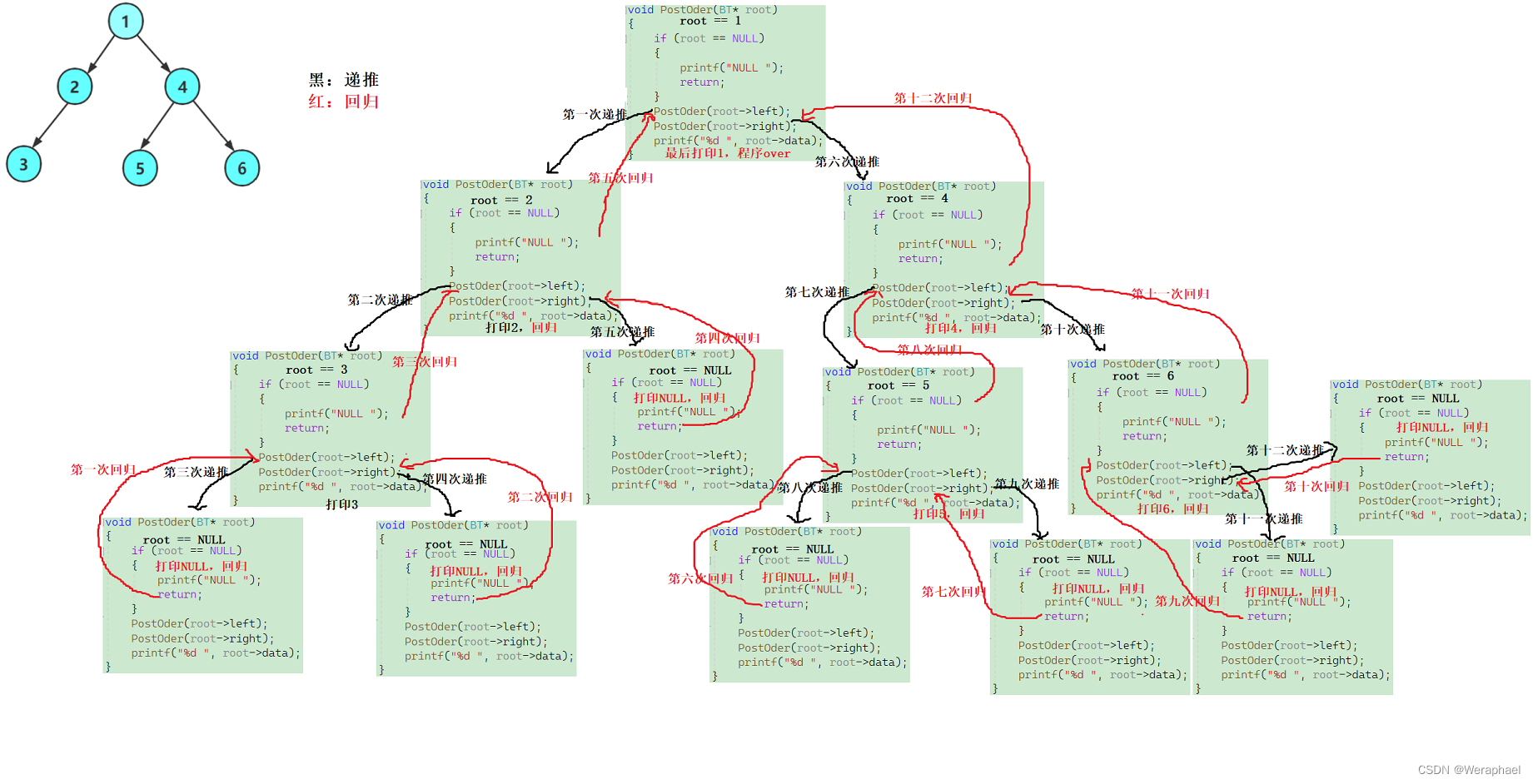
- 根据后序遍历顺序，首先访问左子树 ，而①、②、③都可以作为根，因此先打印③的左子树NULL，再打印③的右子树NULL，最后打印根3
- 接下来，③又作为②的左子树，因此先打印②的右子树NULL，最后再打印根2
- 然后，②又作为①的左子树，因此接下来访问①的右子树。注意，这里不能直接打印4，因为④是可以作为根的，而在访问根之前需要先访问左子树和右子树。所以这里先打印⑤的左子树NULL，再打印⑤的右子树NULL，最后打印根5
- 接下来⑤又作为④的左子树，因此访问④的右子树。注意，这里还是不能打印6，因为6还是可以作为根。所以要先打印⑥的左子树NULL，再打印⑥的右子树NULL，最后再打印根6
- 最后，⑥又作为④的右子树，根据后序遍历的顺序，右子树访问完了就到根了，所以接下来打印根4,；同理，④又作为①的右子树，所以最后打印根1
综上，后序遍历的结果为：
NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
【代码实现】
//后序遍历
void PostOder(BT* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOder(root->left);
PostOder(root->right);
printf("%d ", root->data);
}
int main()
{
BT* root = CreateTree();
//后序遍历
PostOder(root);
printf("
");
return 0;
}
【结果展示】
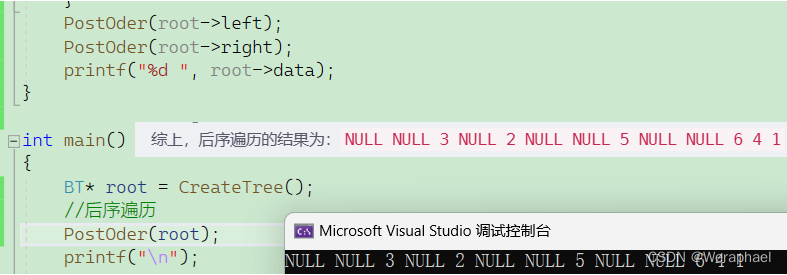
【递归展开图】
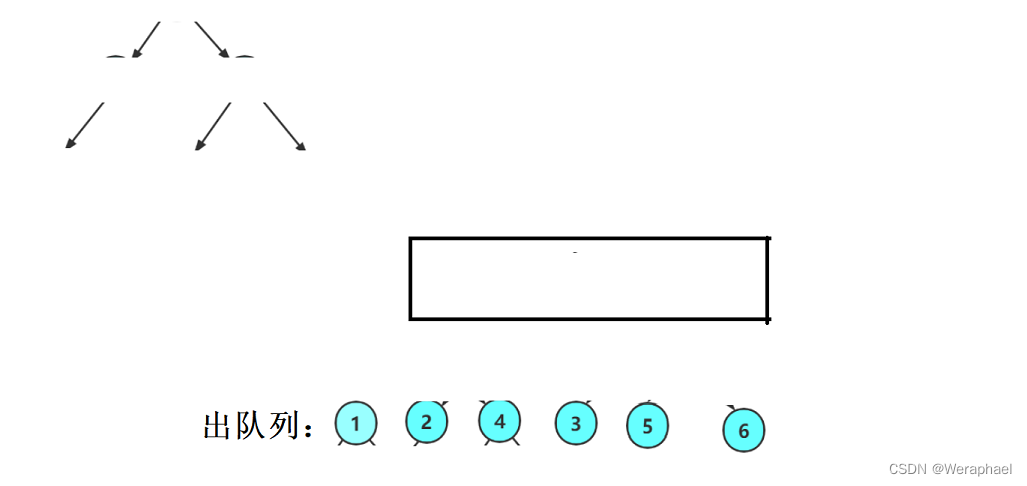
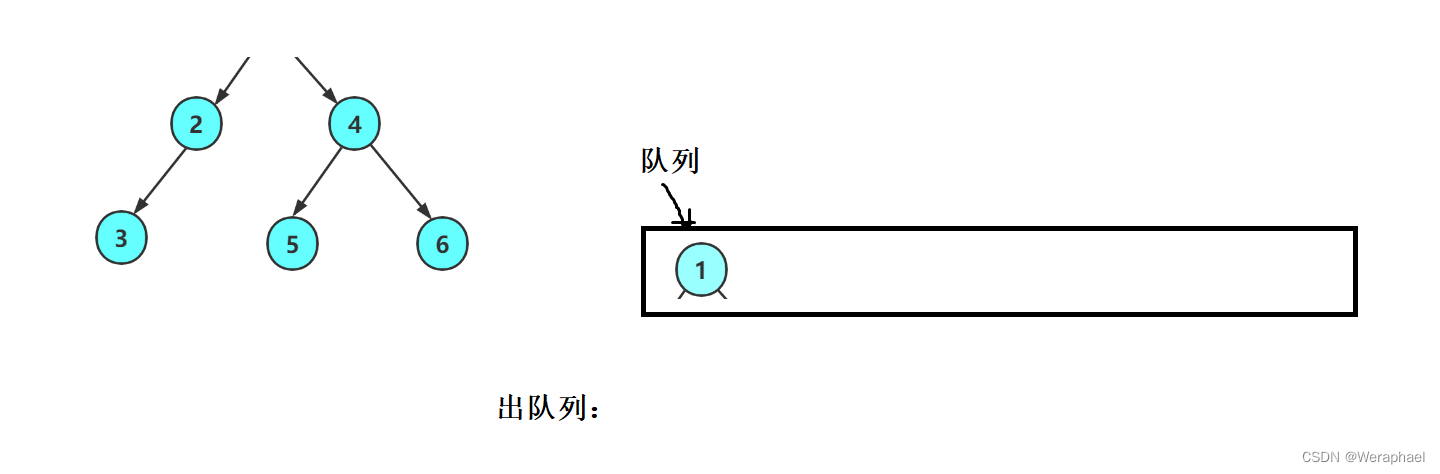
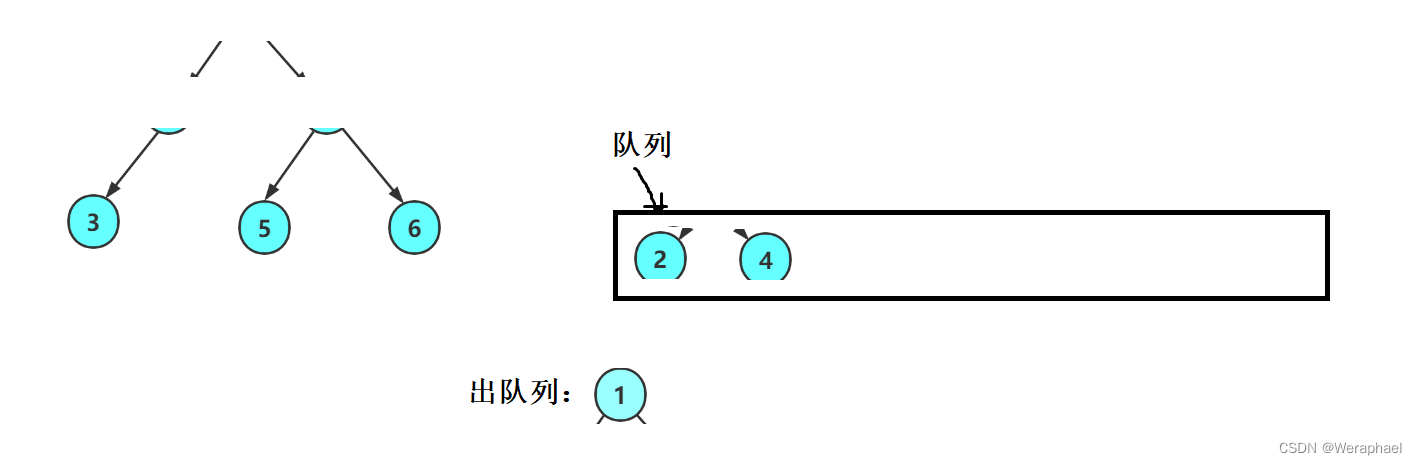
3.14 层序遍历（队列的经典应用）
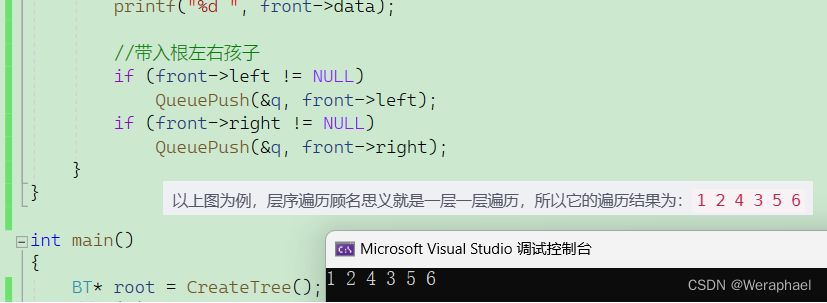
以上图为例，层序遍历顾名思义就是一层一层遍历，所以它的遍历结果为：
1 2 4 3 5 6
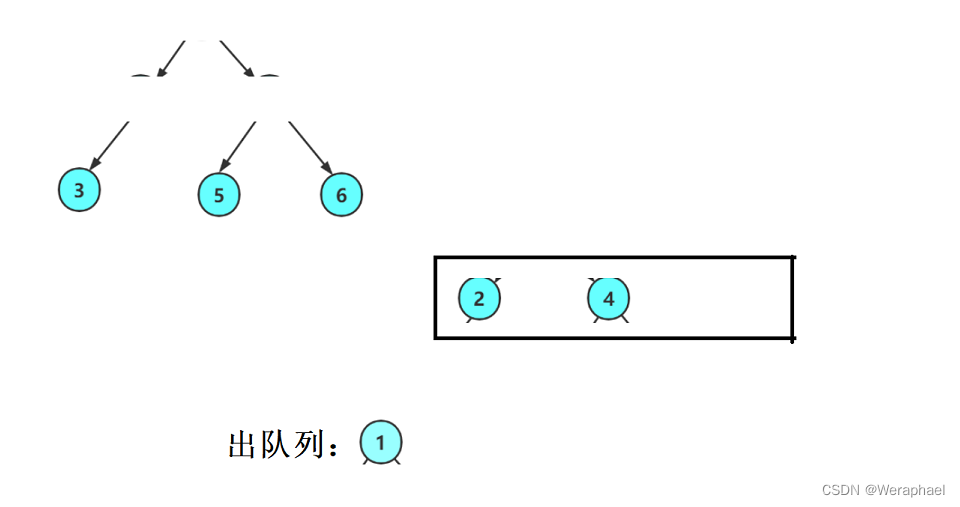
思路：用队列，出上一层，带入下一层
如果树不为空，就先让根结点入队列
然后出队列（打印1），再把1的左孩子和右孩子带入队列
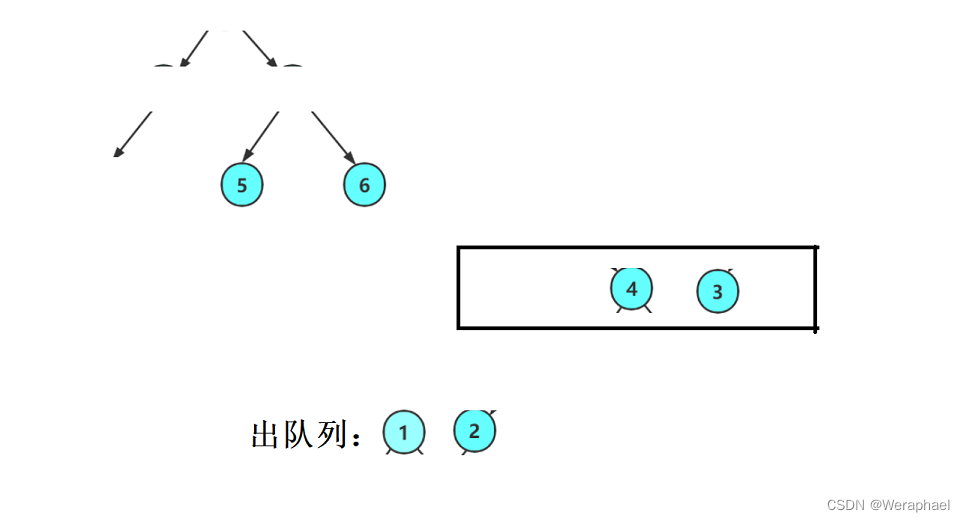
接着让2出队列，再把2的孩子入队列
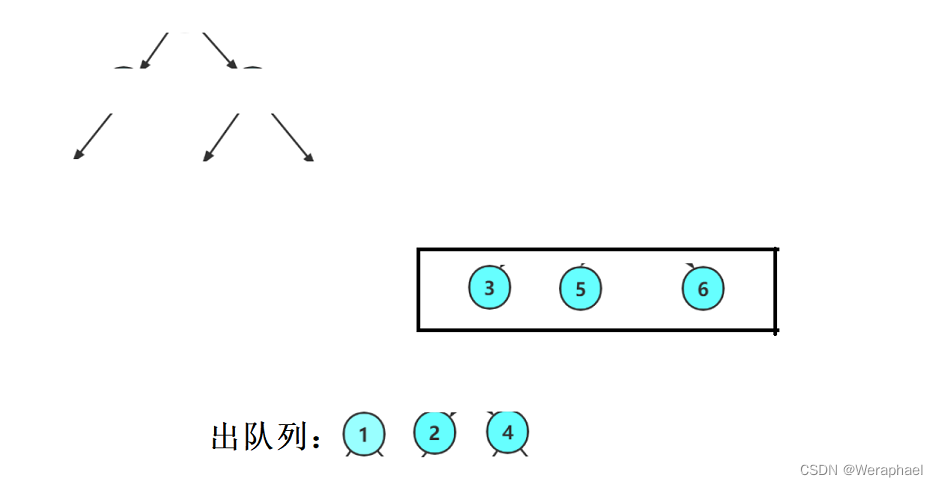
同理，再让4出队列，把它的孩子入队列
最后如果队列不为空，就出队列里的所以元素，即可完成层序遍历
【代码实现】
【Test.c】
//层序遍历
void LevelOrder(BT* root)
{
Queue q;
QueueInit(&q);
//如果树不为空，就入队列
if (root != NULL)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BT* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
//带入根左右孩子
if (front->left != NULL)
QueuePush(&q, front->left);
if (front->right != NULL)
QueuePush(&q, front->right);
}
}
int main()
{
BT* root = CreateTree();
//层序遍历
LevelOrder(root);
printf("
");
return 0;
}
【Queue.h】
typedef struct BinaryTree* DataType;
typedef struct QNode
{
struct QNode* next;
DataType data;
}QNode;
typedef struct Queue
{
QNode* head;
QNode* tail;
int size;
}Queue;
//头指针和尾指针的初始化
void QueueInit(Queue* pq);
//开辟内存空间的销毁
void QueueDestroy(Queue* pq);
//队列的尾插
void QueuePush(Queue* pq, DataType x);
//队列的头删
void QueuePop(Queue* pq);
//队列的大小
int QueueSize(Queue* pq);
//判断队列是否为空
bool QueueEmpty(Queue* pq);
//队头数据
int QueueFront(Queue* pq);
//队尾数据
int QueueBack(Queue* pq);
注意：我们不是往队列存
1 2 4 3 5 6，假设往队列存1,1出来后就带不了它的左右孩子了，因此要存结构体指针
【Queue.c】
//头指针和尾指针的初始化
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
//开辟内存空间的销毁
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur)
{
//在删除当前节点前记录下一个节点
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
pq->size = 0;
}
//队列的尾插
void QueuePush(Queue* pq, DataType x)
{
assert(pq);
//尾插的第一步，先向内存申请空间
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("newnode :: malloc");
return;
}
//再对newnode初始化
newnode->data = x;
newnode->next = NULL;
//接下来开始尾插
//一个问题：当前的链表可能为空
if (pq->head == NULL)
{
//assert括号内为假就报错
//链表为空，表面tail也一定为空（特判）
assert(pq->tail == NULL);
//直接赋值即可
pq->head = pq->tail = newnode;
}
//否则就是正常的尾插
else
{
//tail newnode
pq->tail->next = newnode;
pq->tail = newnode; //更新tail
}
//尾插后size个数+1
pq->size++;
}
//队列的头删
void QueuePop(Queue* pq)
{
assert(pq);
//空链表是不能头删的
assert(pq->head != NULL);
//接下来就是正常的头删
//头删的特殊情况：链表中只有一个节点
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
//记录头节点的下一个节点
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
}
pq->size--;
}
//队列的大小
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->size == 0;
}
//队头数据
int QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
//队尾数据
int QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
【结果展示】
3.2 求二叉树结点个数
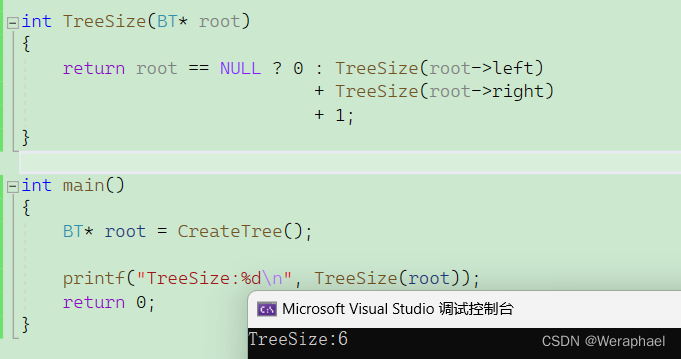
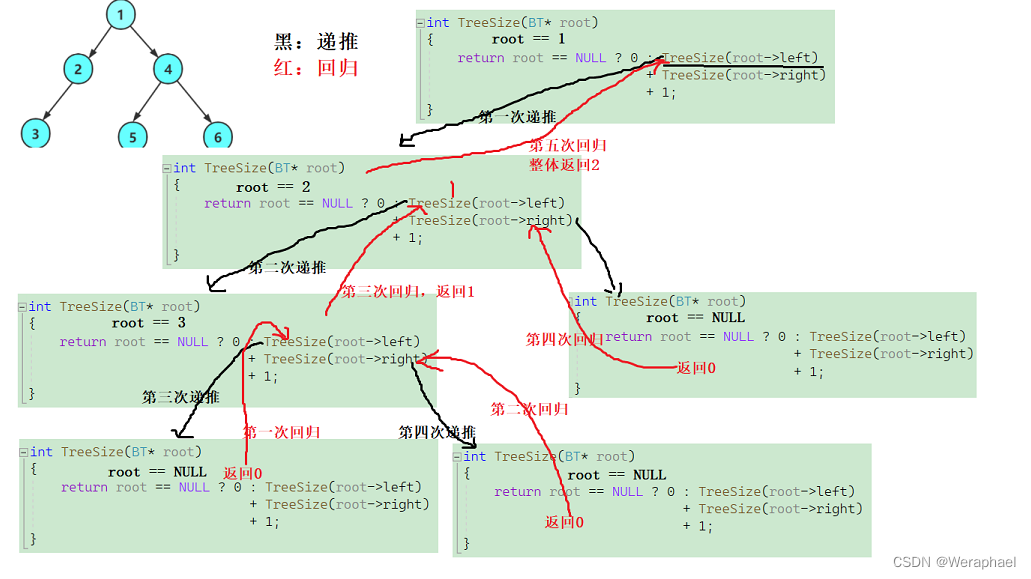
结点个数 = 左子树结点个数 + 右子树结点个数 + 1
【代码实现】
int TreeSize(BT* root)
{
return root == NULL ? 0 : TreeSize(root->left)
+ TreeSize(root->right)
+ 1;
//等价
if (root == NULL)
return 0;
return TreeSize(root->left)
+ TreeSize(root->right)
+ 1;
}
int main()
{
BT* root = CreateTree();
printf("TreeSize:%d
", TreeSize(root));
return 0;
}
【结果展示】
【递归展开图（左半部分）】
3.3 求二叉树的深度
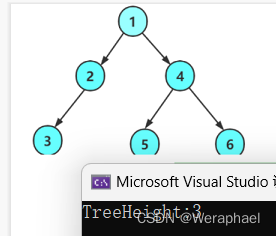
深度 = 左右子树最大的 + 1
【代码实现】
int TreeHeight(BT* root)
{
if (root == NULL)
return 0;
int left = TreeHeight(root->left);
int right = TreeHeight(root->right);
return left > right ? left + 1 : right + 1;
}
int main()
{
BT* root = CreateTree();
printf("TreeHeight:%d
", TreeHeight(root));
return 0;
}
【结果展示】
3.4 求第K层的结点个数
第K层的结点个数 = 左子树的第K - 1层个数 + 右子树的第K - 1层个数
【代码实现】
int TreeKLevel(BT* root, int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}
int main()
{
BT* root = CreateTree();
//求第二层结点个数
printf("TreeKLevel:%d
", TreeKLevel(root, 2));
return 0;
}
【结果展示】
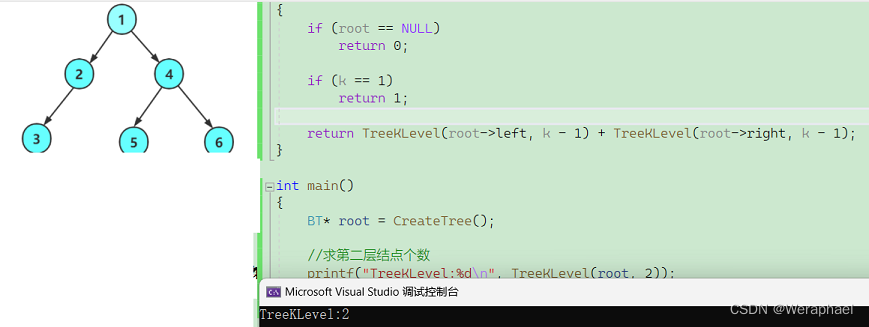
3.5 二叉树查找值为x的节点
前序遍历
【代码展示】
BT* BinaryTreeFind(BT* root, BTreeData x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BT* leftRes = BinaryTreeFind(root->left, x);
if (leftRes)
return leftRes;
BT* RightRes = BinaryTreeFind(root->right, x);
if (RightRes)
return RightRes;
}
int main()
{
BT* root = CreateTree();
//找2这个结点,找到了就打印
BT* res = BinaryTreeFind(root, 2);
printf("%d
", res->data);
return 0;
}
🎈注意：
在BinaryTreeFind函数中，最后的返回不能写成return BinaryTreeFind(root->left, x) || BinaryTreeFind(root->right, x)，原因是函数的返回类型是指针，而或||是运用到bool中的。
【结果展示】
3.6 二叉树的销毁
二叉树的销毁不能从根结点开始，因为假设从根结点开始销毁，后面就找不到根结点的孩子了。
- 正确做法是：
- 先释放左孩子
- 再释放右孩子
- 最后再释放根结点
【代码展示】
void BinaryTreeDestory(BT* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}
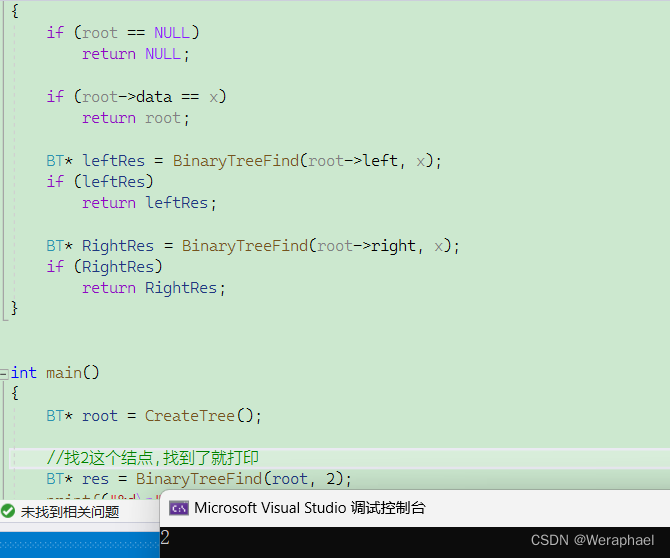
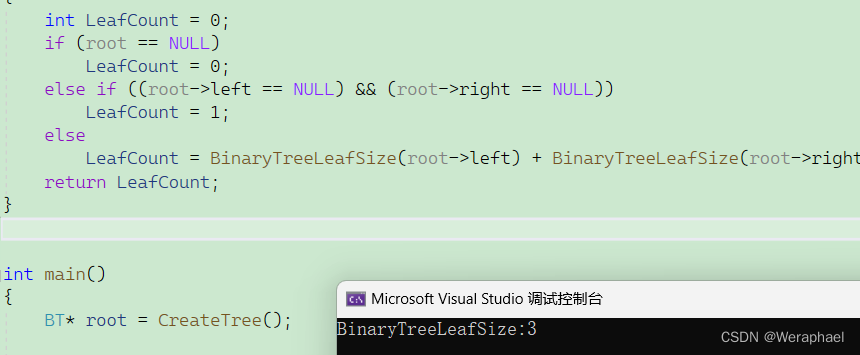
3.7 二叉树叶子结点的个数
叶子结点的特点：左右孩子都为NULL
【代码展示】
int BinaryTreeLeafSize(BT* root)
{
int LeafCount = 0;
if (root == NULL)
LeafCount = 0;
//当左右孩子都为NULL，代表为叶子结点
else if ((root->left == NULL) && (root->right == NULL))
LeafCount = 1;
else
LeafCount = BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
return LeafCount;
}
int main()
{
BT* root = CreateTree();
printf("BinaryTreeLeafSize:%d
", BinaryTreeLeafSize(root));
return 0;
}
【结果展示】
3.8 构建二叉树
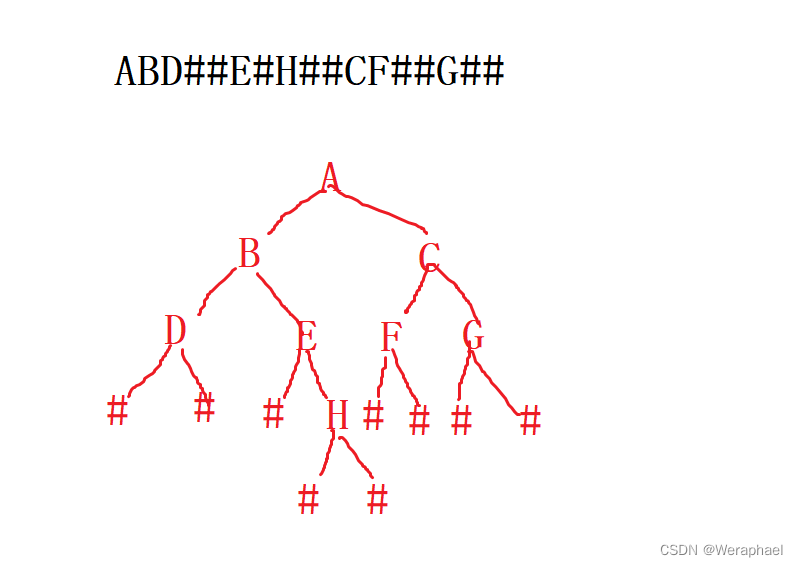
- 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
思路：
通过前序遍历
根 左子树 右子树，画出二叉树如下图
【代码实现】
BinaryTree* CreateTree(char* a, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BinaryTree* root = (BinaryTree*)malloc(sizeof(BinaryTree));
assert(root);
root->data = a[*pi];
(*pi)++;
root->left = CreateTree(a, pi);
root->right = CreateTree(a, pi);
return root;
}
int main()
{
char a[100];
scanf("%s", a);
//建树
int i = 0;
BinaryTree* root = CreateTree(a, &i);
return 0;
}
- 为什么
i要传地址？
因为每调用一次递归，栈帧的i都是不同的，但为了在每次调用的时候，都精确用到数组内的元素，因此要传地址。
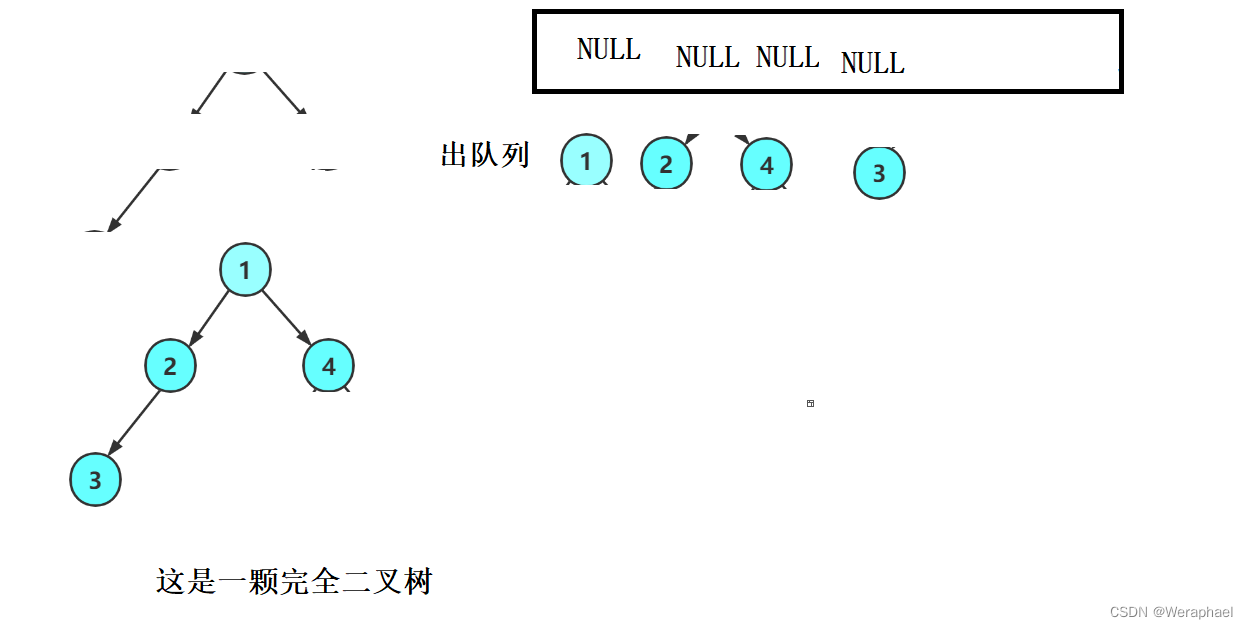
3.9 判断二叉树是否是完全二叉树
首先完全二叉树的性质是：假设有
H层，前H - 1必须是满的，且最后一层必须是连续的。
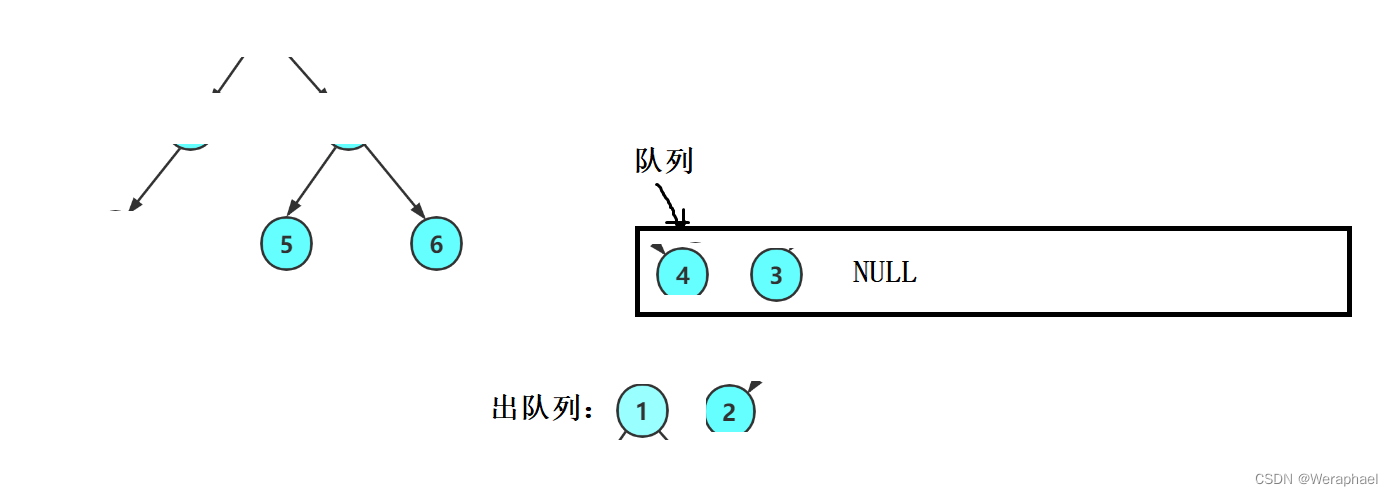
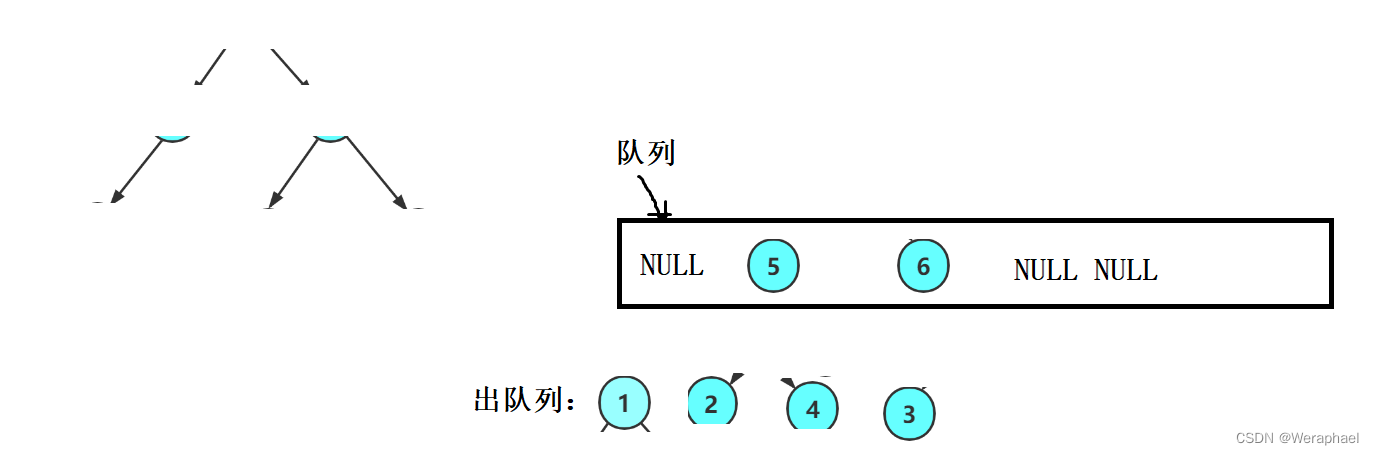
所以，按层序遍历走，非空结点一定是连续的
【流程图】
- 按照层序遍历，只要根不为空入队列
- 出队列元素1时，需要带其左孩子2和右孩子4入队列
- 同样的道理，出队列元素2时，将其左孩子3和NULL带入队列
- 重复以上操作，直到出队列的元素为NULL
- 如上图所示，队列内的NULL后面还存在非空元素，这就说明它不是完全二叉树。如果是完全二叉树，当出队列的元素为NULL，后面有应该都是NULL，不信我举个例子（如下图）
【代码展示】
bool TreeComplete(BT* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BT* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
else
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
// 判断是不是完全二叉树
while (!QueueEmpty(&q))
{
BT* front = QueueFront(&q);
QueuePop(&q);
// 后面有非空，说明非空节点不是完全连续
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
int main()
{
BT* root = CreateTree();
if (TreeComplete(root))
printf("是完全二叉树
");
else
printf("不是完全二叉树
");
return 0;
}
【结果展示】
四、总结
以上就是本章的所以内容了，如果大家有什么疑问或意见，欢迎评论区留言~
最后，如果大家能给我点个赞和关注，那我会很高兴的hh~
风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。
站长推荐
- U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效)