单链表OJ题：LeetCode--142.环形链表Ⅱ（判断第一次入环的节点）网站首页 技术教程

单链表OJ题：LeetCode--142.环形链表Ⅱ（判断第一次入环的节点）

stackY、 2024-09-10 00:01:04

简介单链表OJ题：LeetCode--142.环形链表Ⅱ（判断第一次入环的节点）

朋友们、伙计们，我们又见面了，本期来给大家解读一下LeetCode中第142道单链表OJ题，如果看完之后对你有一定的启发，那么请留下你的三连，祝大家心想事成！

数据结构与算法专栏：数据结构与算法

个人主页 ：stackY、

C 语言专栏：C语言：从入门到精通

LeetCode--142.环形链表Ⅱ： https://leetcode.cn/problems/linked-list-cycle-ii/description/

1.题目介绍

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改链表。

2.实例演示

3.解题思路

小编在这里给大家推荐比较简单的解题思路，同样的都是使用快慢指针的，我们先来讲具体的解题思路，后面会验证这种方法的正确性：

同样的还是设置快慢指针，慢指针一次走一步，快指针一次走两步，同样的我们先来判断链表是否有环（如何判断链表有环大家可以去看LeetCode：141.环形链表这篇博客，里面包含了具体解题思路），在判断是否有环之后呢，我们要找到第一次入环的节点，那这个就比较麻烦了，该怎么找呢？小编在这里给大家提供一个简单的解法：记录环中快慢指针相遇的节点（meet），然后让一个指针从链表的头（head）开始走，一次都走一步，当meet和head相遇时它们就是第一次入环的节点。

代码演示：
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) {
    //设置快慢指针
    struct ListNode* slow = head;
    struct ListNode* fast = head;
    //快慢指针的相遇节点
    struct ListNode* meet = NULL;

    //判断是否有环
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        //若有环则记录快慢指针的相遇节点
        if(fast == slow)
        {
            meet = slow;
            //找第一次入环的节点
            while(meet != head)
            {
                //一次都走一步
                meet = meet->next;
                head = head->next;
            }

            return meet;
        }
    }
    //无环则返回NULL
    return NULL;
}

4.思路验证

要求环形链表第一次入环的节点，我们使用的这种快慢指针的方法是很简单的，也是很巧妙的，这种方法具体是怎么实现的，让我们接着往下来看：

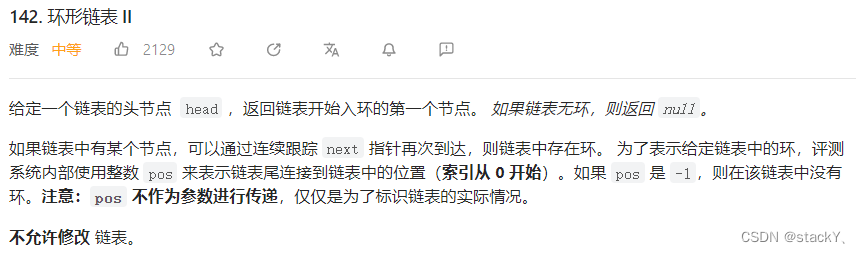
我们假设环的长度为C，链表的头到第一次入环节点的距离为L，第一次入环的节点到相遇点的距离为X。

慢指针在这里有一个分析问题：slow有没有可能在环里面转了好几圈快指针才追上？

答案是肯定不可能，因为快指针的速度是慢指针的2倍，不存在错过的情况，所以慢指针不存在走好几圈才能被快指针追上的情况。

很多老铁在这里验证的时候使用了一种错误的验证方法：

慢指针slow走的路程是：L + X

快指针fast走的路程是：L + X + C

那么就有一种对应的关系：2 * （L + X） = L + X + C

L = C - X

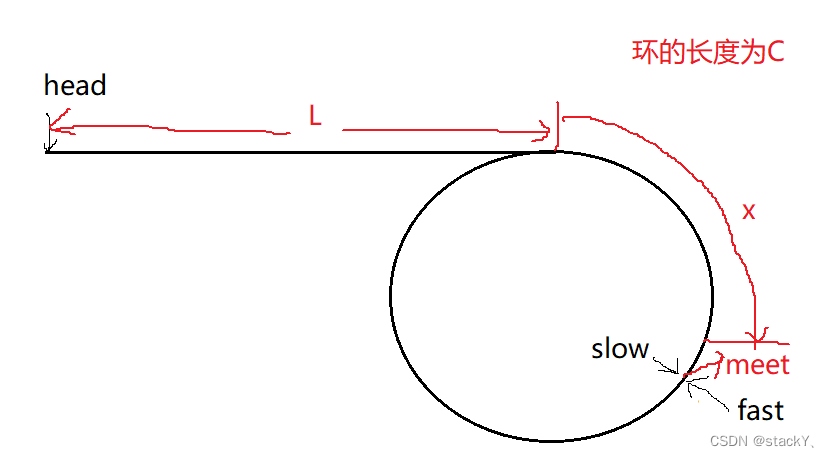
这种方法有一个弊端，比如一个环形链表前面进环的路程(L)非常的长，而环(C)又非常的小，那这就出现问题了：

所以呢我们可以将这种特殊的情况考虑进去，那么我们应该先算快指针fast走的路程：

快指针fast走的路程：L + n * C + X（n为慢指针进环之前快指针在环里面走过的圈数）

慢指针slow走的路程是：L + X

那么就有一种对应的关系： 2 * （L + X） = L + X + n * C

L = n * C - X

那么这样解释起来就好多了，相遇节点到第一次入环的节点的距离为C - X

头节点到第一次入环节点的距离为L，那么根据 L = n * C - X这个对应关系，就可以推出从相遇节点每次走一步，头指针每一次走一步，当它们两个相遇的时候就是这个环形链表第一次入环的节点。

5.其他解题方法

除了上面我们验证的这个方法外，还有另外的一种方法，小编在这里只说思路，感兴趣的老铁可以自己尝试一下：

分割环形链表法：

可以记录快慢指针的相遇节点，然后以这个相遇点为起点，保存并记录相遇节点的下一个节点，然后将相遇节点和它的下一个节点断开链接，将这个环一分为二，这时就转换成了链表相交的问题。

一个链表是从头开始，另一个链表的头是从相遇点的下一个节点，那么这两个链表的相交节点就是第一次入环的节点。

感兴趣的老铁可以自己动手写一下完整的代码。