该专栏内容为对该视频的学习记录：【《PyTorch深度学习实践》完结合集】
专栏的全部代码、数据集和课件全放在个人GitHub了，欢迎自取。

1 Inception Module

GoogLeNet（又称为Inception-v1）是由谷歌公司在2014年提出的一个卷积神经网络架构，它是当时ImageNet图像识别挑战赛的冠军，其准确性超过了以往所有的卷积神经网络架构。

GoogLeNet主要的创新在于使用了一个名为“Inception”的模块，这个模块使用了多个不同尺寸的卷积核和池化核，从而可以在不同的尺度上提取图像特征。通过将多个Inception模块串联在一起，可以构建一个非常深的卷积神经网络，同时保持计算效率和准确性。

除了Inception模块之外，GoogLeNet还采用了一些其他的技术来提高模型的准确性，比如使用全局平均池化层来代替全连接层，从而减少模型参数数量，防止过拟合等等。GoogLeNet的成功启示了后来很多卷积神经网络架构的设计，也成为了深度学习领域的一个里程碑。

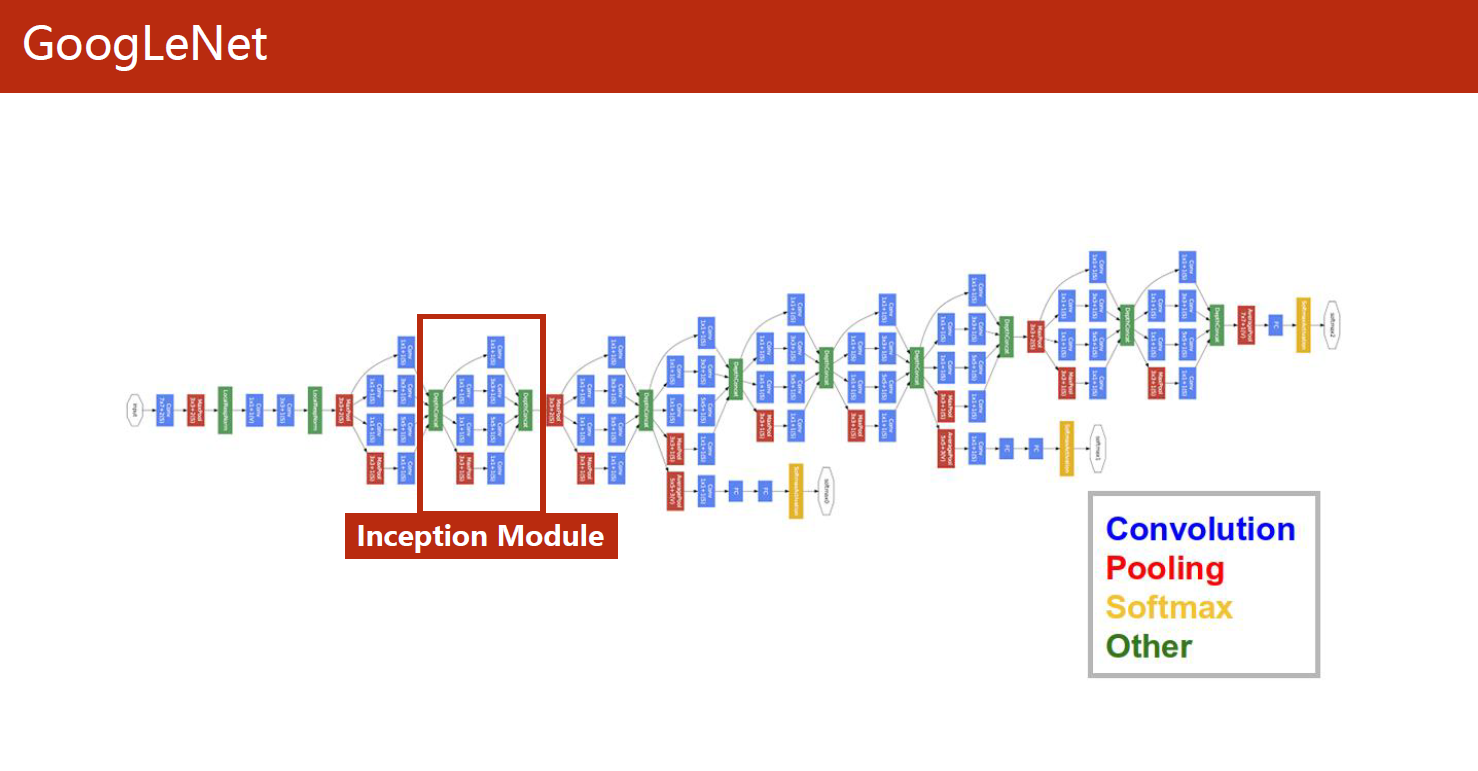
在Inception中有许多1×1的卷积核：

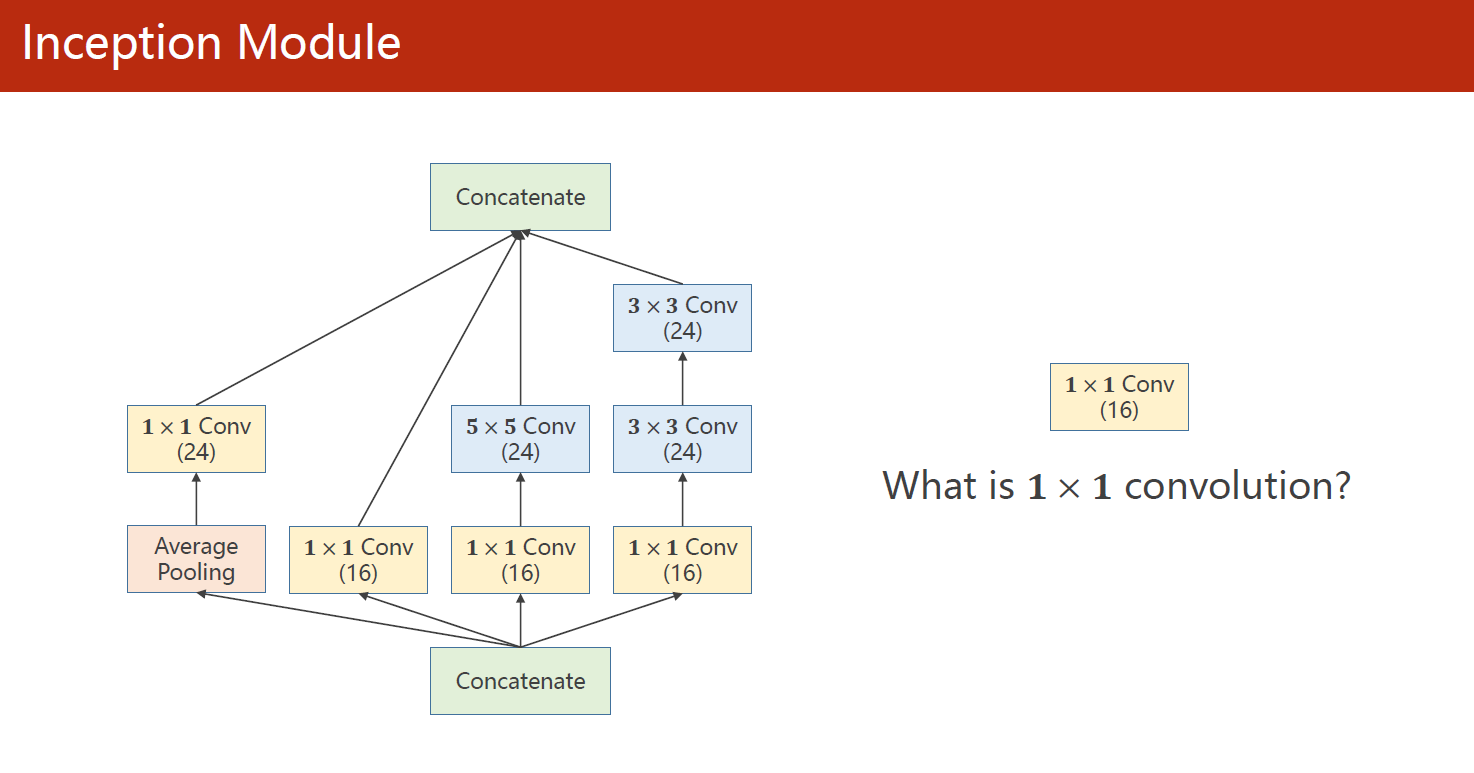
1.1 1×1卷积

在Inception网络中，1x1卷积核起到了非常重要的作用。它通常被用于在通道（channel）维度上进行降维和升维的操作，可以将输入特征图的通道数进行压缩或扩展，从而减少模型的计算复杂度和参数数量，提高计算效率和准确性。

具体来说，使用1x1卷积核可以实现以下两种操作：

1. 通道的降维：将输入特征图的通道数减少，从而减小模型参数的数量，提高计算效率。这种操作通常在Inception网络中的“线性池化”（bottleneck）结构中使用，它先使用1x1卷积核对输入特征图进行降维，然后再应用较大的卷积核进行特征提取。
2. 通道的升维：将输入特征图的通道数扩展，从而增加模型的表示能力。这种操作通常在Inception网络中的“inception模块”中使用，它先使用1x1卷积核将输入特征图的通道数进行扩展，然后再使用不同尺寸的卷积核进行特征提取。

通过使用1x1卷积核，Inception网络可以实现在不同尺度上提取特征，从而提高模型的准确性和计算效率。

计算示例：下图为把三通道的输入变成一通道的输出

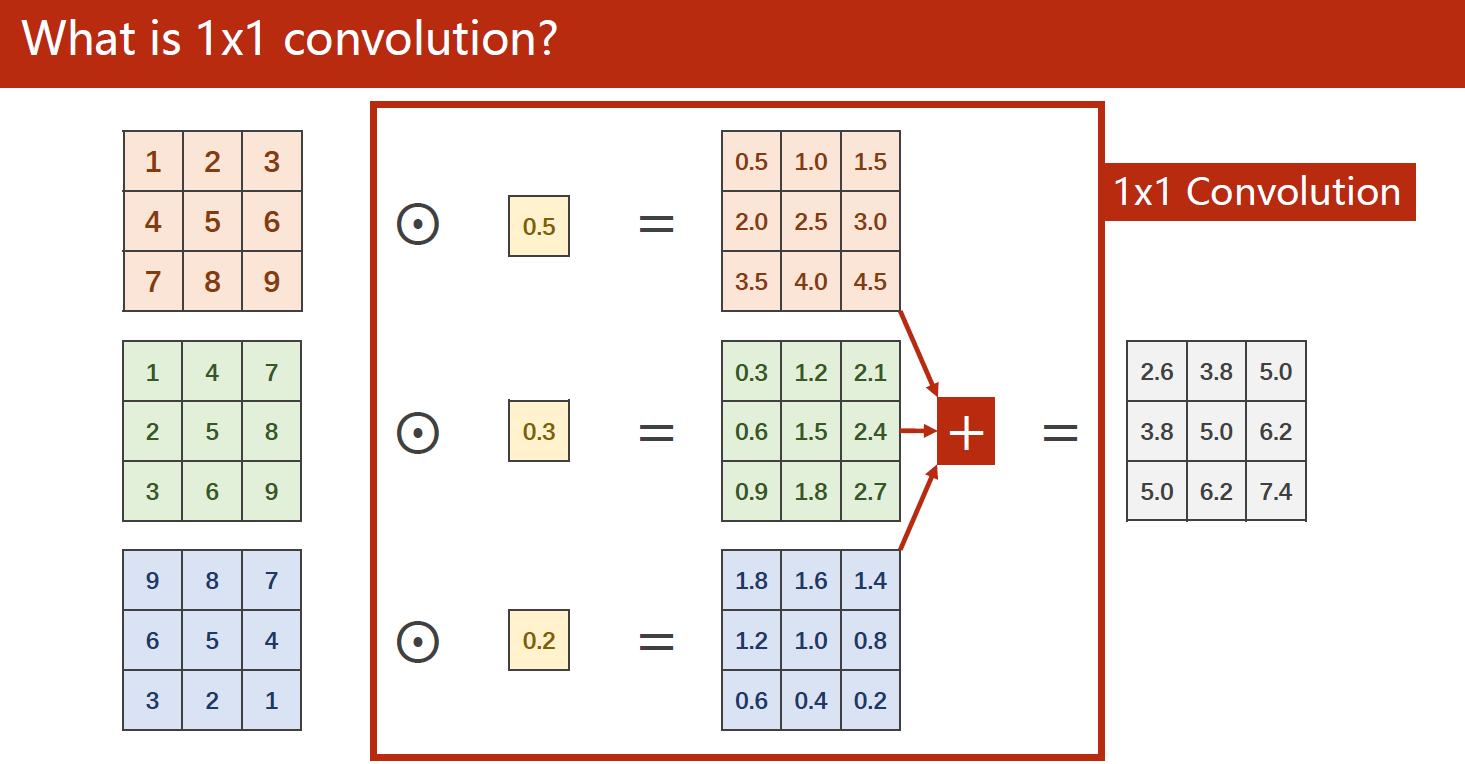
在减少计算复杂程度上，相同形状的输出结果减少了接近一个数量级：

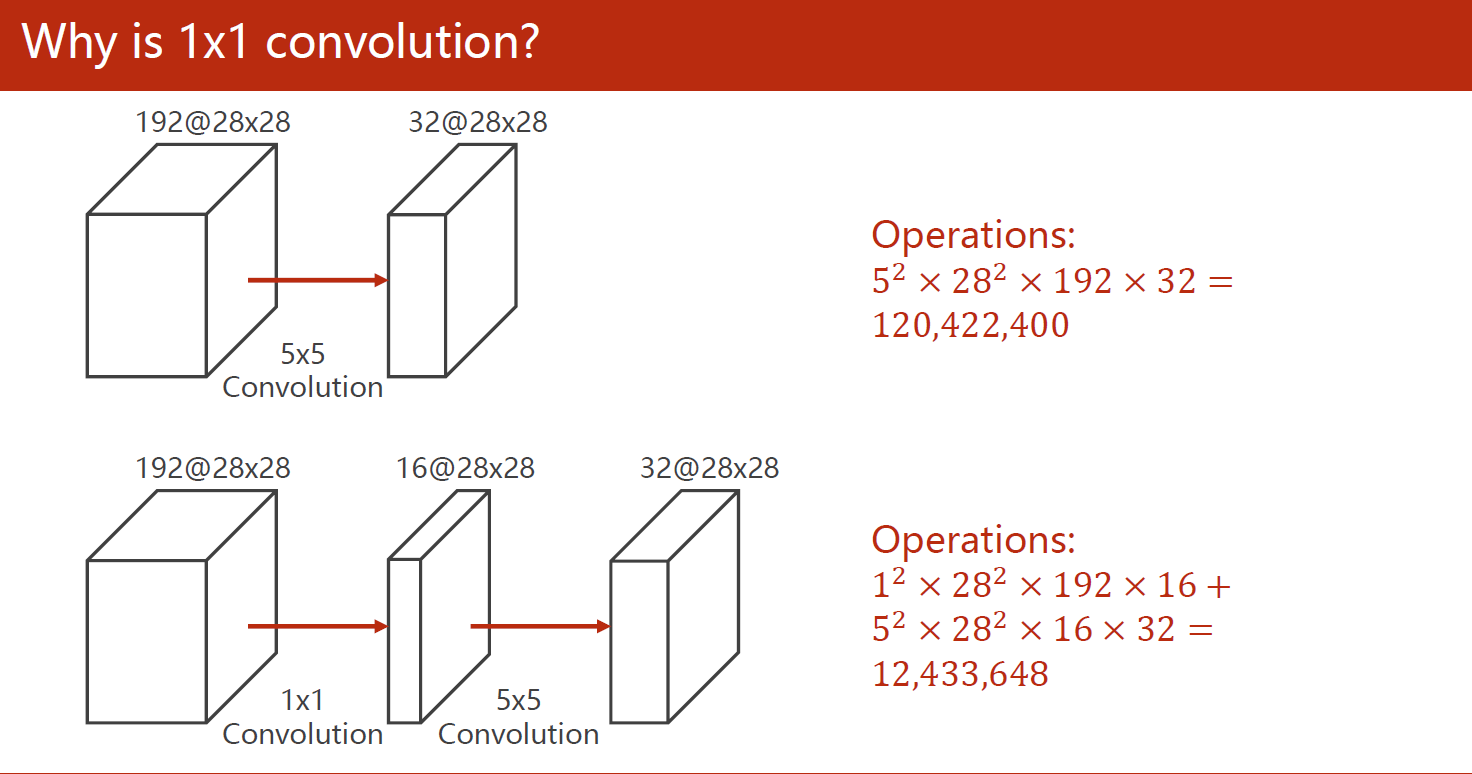
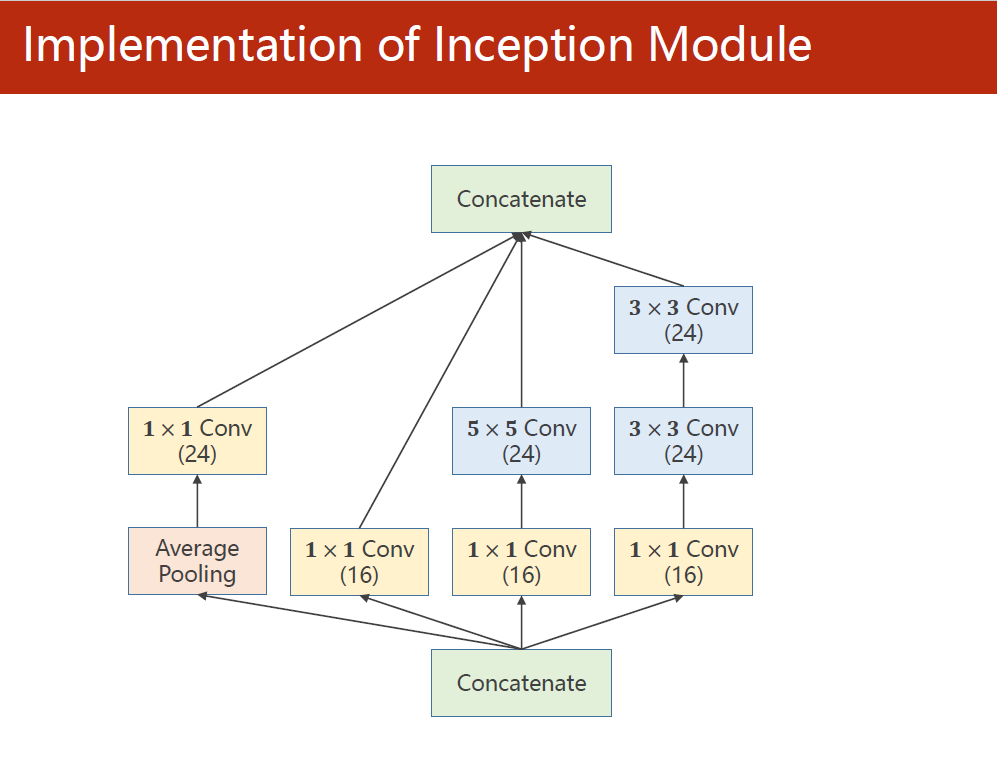
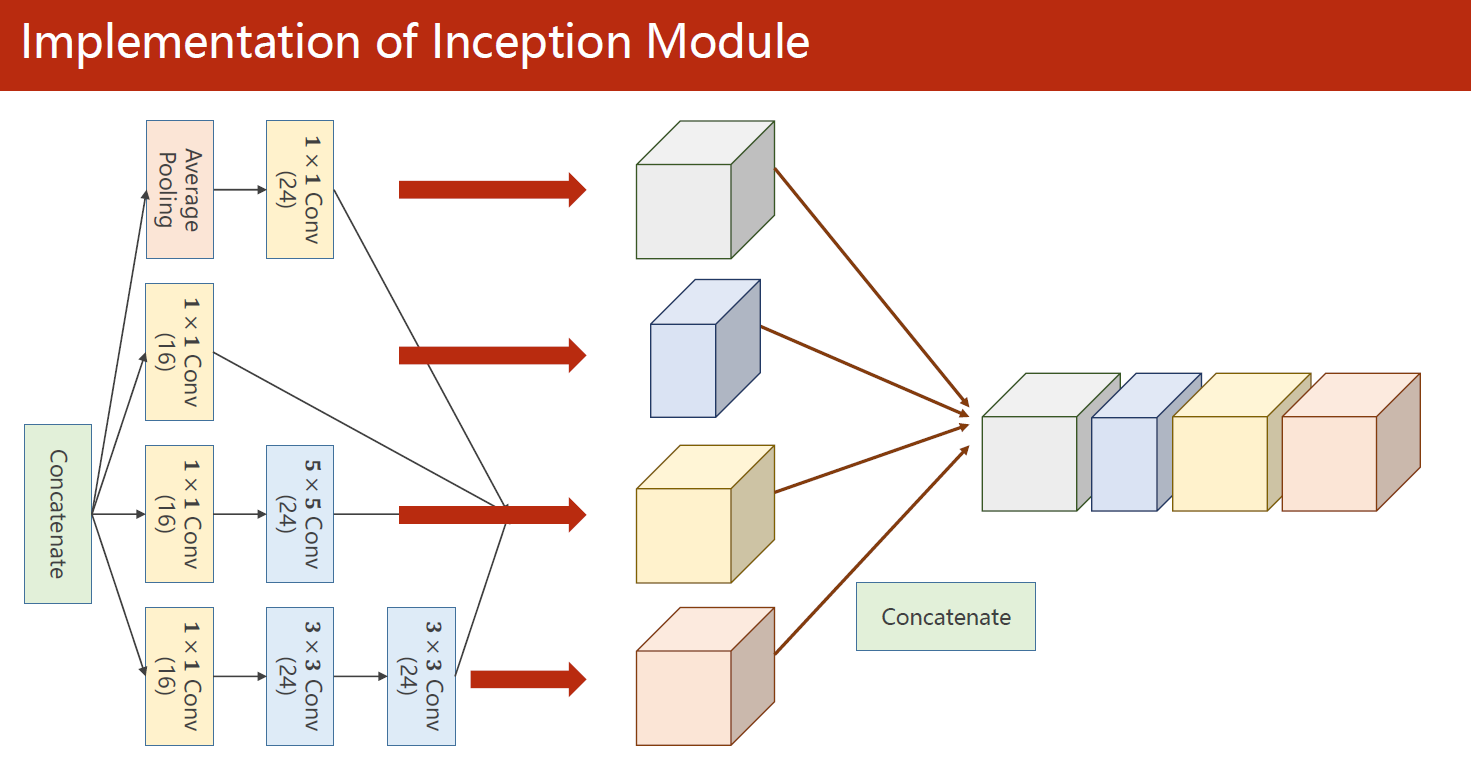
1.2 Inception模块结构

内部结构：在四个分支各自产生的输出根据通道维度拼接成该Inception块的输出。

1.3 完整代码

这段代码的作用是定义了一个卷积神经网络模型，并准备了MNIST数据集进行训练。

具体来说，代码的主要功能如下：

1. 通过torchvision库中的transforms模块，定义了一系列对MNIST数据集进行预处理的操作，包括将图片转换为Tensor类型，以及对Tensor进行标准化处理，使得数据的取值范围在[0,1]之间，并减去均值0.1307，除以标准差0.3081。
2. 使用torchvision库中的datasets模块，分别准备了训练集和测试集，并通过DataLoader函数将它们打包成了可迭代的数据集对象，方便进行批量训练和测试。
3. 定义了Inception块类InceptionA，它包含了4个分支，分别进行了不同的卷积操作，并将它们在通道维度上进行了拼接。其中，第1个分支为1x1卷积，第2个分支为1x1卷积 + 5x5卷积，第3个分支为1x1卷积 + 3x3卷积 + 3x3卷积，第4个分支为1x1卷积 + 平均池化。最终输出通道数为88。
4. 定义了卷积神经网络模型Net，包含了2个卷积层、2个Inception块、1个最大池化层和1个全连接层。其中，第1个卷积层的输入通道数为1，输出通道数为10，卷积核大小为5；第2个卷积层的输入通道数为88，输出通道数为20，卷积核大小为5；第1个Inception块的输入通道数为10，输出通道数为88；第2个Inception块的输入通道数为20，输出通道数为88；最大池化层的核大小为2；全连接层的输入大小为1408，输出大小为10。
5. 在forward函数中，定义了模型的前向传播过程，包括了卷积、Inception块、池化和全连接层。其中，卷积和Inception块的输出使用ReLU作为激活函数，最终输出使用Softmax函数进行归一化。
6. 在训练过程中，使用交叉熵损失函数作为评价指标，使用SGD优化器进行参数优化，训练次数为10个epoch。最终得到的模型在测试集上的准确率为98.97%。

import torch
import torch.nn.functional as F
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

# 1、准备数据集
batch_size = 64
transform = transforms.Compose([  # 一系列的操作，Compose将其组合在一起
    transforms.ToTensor(),  # 将图片转换为Tensor
    transforms.Normalize((0.1307,), (0.3081,))  # 标准化到[0,1]，均值和方差
])
train_dataset = datasets.MNIST(root='../P6 逻辑斯谛回归/data', train=True,
                               download=False,  # 在P6 逻辑斯谛回归中我已下载，这里不用下载了
                               transform=transform)
test_dataset = datasets.MNIST(root='../P6 逻辑斯谛回归/data', train=False, download=False, transform=transform)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)  # 测试集设置为False，方便观察结果


# 2、设计模型

# 2.1 设计Inception块
class InceptionA(torch.nn.Module):
    def __init__(self, in_channels):  #in_channels为输入通道数
        super(InceptionA, self).__init__()
        self.branch1x1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)  # 1x1卷积

        self.branch5x5_1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)  # 1x1卷积
        self.branch5x5_2 = torch.nn.Conv2d(16, 24, kernel_size=5, padding=2)  # 5x5卷积，padding=2保证输入输出大小一致

        self.branch3x3_1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)  # 1x1卷积
        self.branch3x3_2 = torch.nn.Conv2d(16, 24, kernel_size=3, padding=1)  # 3x3卷积，padding=1保证输入输出大小一致
        self.branch3x3_3 = torch.nn.Conv2d(24, 24, kernel_size=3, padding=1)  # 3x3卷积

        self.branch_pool = torch.nn.Conv2d(in_channels, 24, kernel_size=1)  # 1x1卷积

    def forward(self, x):
        branch1x1 = self.branch1x1(x)  # 1x1卷积处理

        branch5x5 = self.branch5x5_1(x)
        branch5x5 = self.branch5x5_2(branch5x5)  # 5x5卷积处理

        branch3x3 = self.branch3x3_1(x)
        branch3x3 = self.branch3x3_2(branch3x3)
        branch3x3 = self.branch3x3_3(branch3x3)

        # 最大池化torch.nn.MaxPool2d()是一个类，而这里的平均池化F.avg_pool2d()是一个函数
        branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)  # 平均池化处理,这里的padding=1,保证输入输出大小一致
        branch_pool = self.branch_pool(branch_pool)

        # 将四个分支的输出在通道维度上进行拼接
        outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
        return torch.cat(outputs, dim=1)  # dim=1表示在通道维度上进行拼接


# 2.2 设计网络
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 卷积层
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(88, 20, kernel_size=5)  #这里的88是Inception块的输出通道数

        # 实例化Inception块，返回结果为88通道，因为Inception块中有四个分支，每个分支输出通道数为16+24+24+24=88
        self.incep1 = InceptionA(in_channels=10)
        self.incep2 = InceptionA(in_channels=20)

        self.mp = torch.nn.MaxPool2d(2)  # 池化层
        self.l1 = torch.nn.Linear(1408, 10)  # 全连接层,不确定第一个参数为多少时，可以先随便写一个，然后运行程序，看报错信息

    def forward(self, x):
        # Flatten data from (n, 1, 28, 28) to (n, 784)
        batch_size = x.size(0)  #获取batch_size,这里的batch_size=64
        x = F.relu(self.mp(self.conv1(x)))  # 经过第一个卷积层+池化层+激活函数
        x = self.incep1(x)  #经过第一个Inception块处理
        x = F.relu(self.mp(self.conv2(x)))  # 经过第二个卷积层+池化层+激活函数
        x = self.incep2(x)  #经过第二个Inception块处理
        x = x.view(batch_size, -1)  # 将数据展平，方便全连接层处理
        x = self.l1(x)  # 全连接层
        return x


model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")  # 判断是否有GPU加速
model.to(device)  # 将模型放到GPU上

# 3、构建损失和优化器
criterion = torch.nn.CrossEntropyLoss()  # 交叉熵损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 优化器,lr为学习率，momentum为动量


# 4、训练和测试
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, labels = data
        inputs, labels = inputs.to(device), labels.to(device)  # 将数据放到GPU上
        optimizer.zero_grad()  # 梯度清零
        # forward + backward + update
        outputs = model(inputs)  # outputs并不是概率，而是线性层的输出，但其大小顺序与概率分布相同
        loss = criterion(outputs, labels)
        loss.backward()  # 反向传播
        optimizer.step()  # 更新参数

        running_loss += loss.item()
        if batch_idx % 300 == 299:  # 每300个batch打印一次平均loss
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0
    total = 0
    with torch.no_grad():  # 测试过程中不需要计算梯度
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)  # 将数据放到GPU上
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)  # 返回每一行中最大值的那个元素，以及其索引
            total += labels.size(0)  # labels的size为[64]，即64个样本
            correct += (predicted == labels).sum().item()  # 统计预测正确的样本个数
    accuracy = 100 * correct / total
    accuracy_list.append(accuracy)
    print('Accuracy on test set: %d %%' % accuracy)


if __name__ == '__main__':
    accuracy_list = []
    for epoch in range(10):
        train(epoch)
        test()
    plt.plot(accuracy_list)
    plt.xlabel('epoch')
    plt.ylabel('accuracy')
    plt.grid()
    plt.show()

[1,   300] loss: 0.950
[1,   600] loss: 0.229
[1,   900] loss: 0.170
Accuracy on test set: 96 %
[2,   300] loss: 0.123
[2,   600] loss: 0.118
[2,   900] loss: 0.098
Accuracy on test set: 97 %
[3,   300] loss: 0.083
[3,   600] loss: 0.083
[3,   900] loss: 0.078
Accuracy on test set: 97 %
[4,   300] loss: 0.070
[4,   600] loss: 0.061
[4,   900] loss: 0.065
Accuracy on test set: 98 %
[5,   300] loss: 0.055
[5,   600] loss: 0.060
[5,   900] loss: 0.058
Accuracy on test set: 98 %
[6,   300] loss: 0.052
[6,   600] loss: 0.051
[6,   900] loss: 0.050
Accuracy on test set: 98 %
[7,   300] loss: 0.043
[7,   600] loss: 0.046
[7,   900] loss: 0.048
Accuracy on test set: 98 %
[8,   300] loss: 0.042
[8,   600] loss: 0.041
[8,   900] loss: 0.045
Accuracy on test set: 98 %
[9,   300] loss: 0.036
[9,   600] loss: 0.039
[9,   900] loss: 0.041
Accuracy on test set: 98 %
[10,   300] loss: 0.030
[10,   600] loss: 0.041
[10,   900] loss: 0.038
Accuracy on test set: 98 %

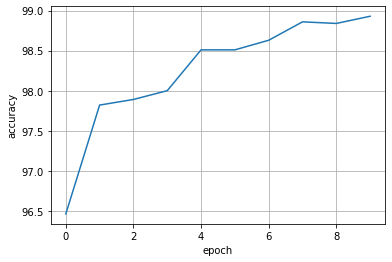
从图像可以看出，在epoch为10时，模型的准确率已经非常接近99%，并且还有上升的趋势，说明Inception块的引入使得模型的预测能力更强了。

同样地，我把epoch加到30，白嫖Kaggle的GPU跑出的结果如下图：

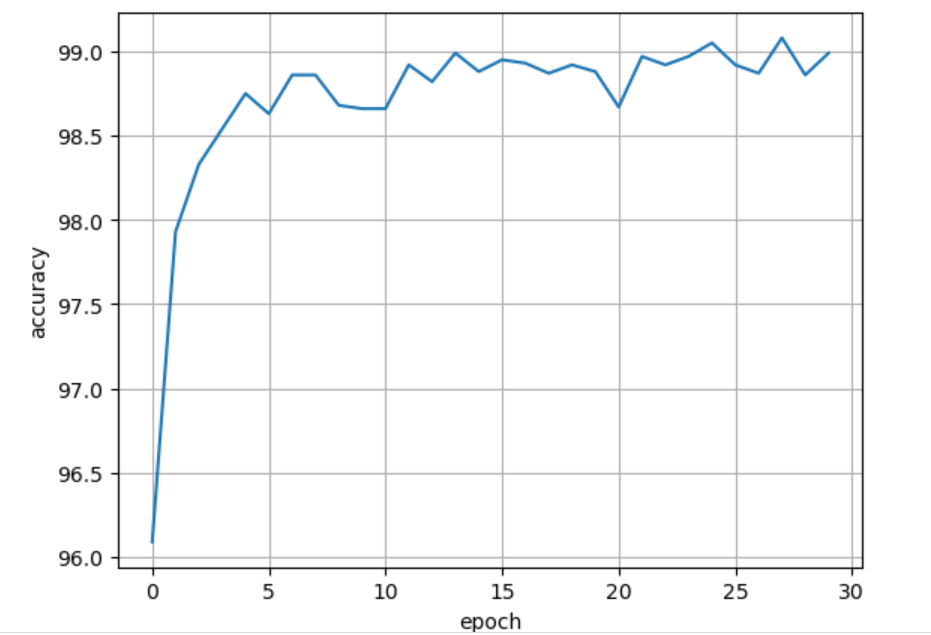
可见，结果一直在99%上下波动。

2 残差网络(Residual Network)

Residual Network（ResNet）是一种深度神经网络结构，它的作用是解决深度神经网络中的梯度消失和梯度爆炸问题。这些问题会在网络层数增加时出现，导致训练变得困难甚至无法收敛。

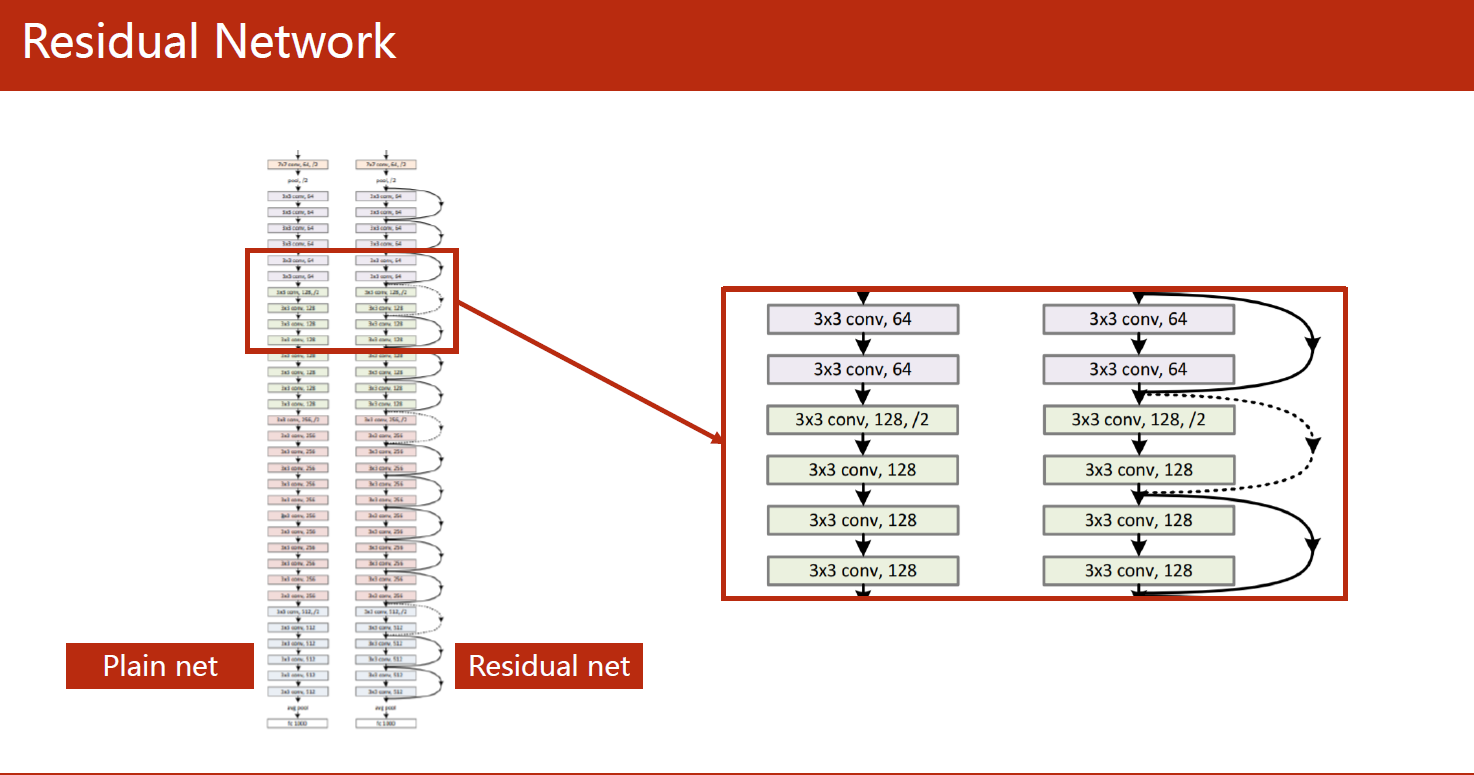
ResNet通过引入残差连接（residual connection）来解决这个问题。残差连接是指将网络的输入直接添加到网络的输出中，形成一个“shortcut”，使得在梯度反向传播时可以更容易地通过残差连接跳过一些层的信息，减轻了梯度消失和梯度爆炸的问题。同时，这种残差连接也使得网络能够更深，提高了模型的准确性和泛化能力。

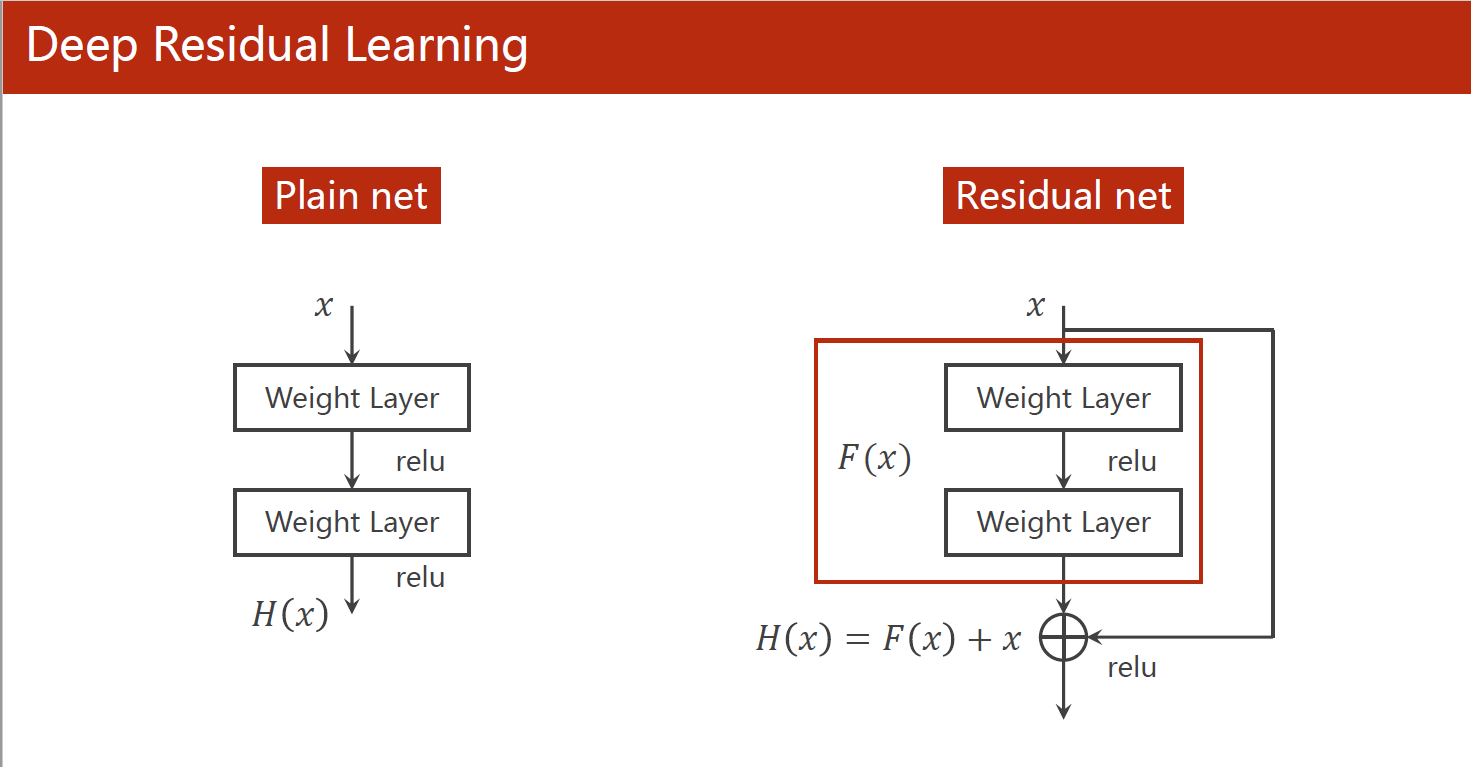
ResNet的另一个作用是实现了端到端的训练，这意味着整个模型可以通过反向传播进行端到端的训练，而无需进行手动的特征工程和预训练。这大大简化了模型的训练流程和实现难度，也提高了模型的效率和准确性。

下面这段代码是一个使用PyTorch实现的残差网络模型，在MNIST数据集上进行训练和测试。主要步骤包括：

1. 数据集准备：使用torchvision.datasets加载MNIST数据集，并进行数据预处理（转为Tensor，标准化），然后使用torch.utils.data.DataLoader将数据集分成小批次进行加载。
2. 模型设计：包含一个卷积层、两个残差块和一个全连接层。残差块采用两个卷积层，输入输出通道数一致，并通过加上输入再经过激活函数的方式来保证维度一致。卷积层和全连接层采用ReLU作为激活函数。
3. 损失函数和优化器：采用交叉熵损失函数，优化器采用SGD，并在训练过程中使用动量。
4. 训练和测试：采用mini-batch SGD来训练模型，每300个batch打印一次平均loss。训练完成后，使用测试集来评估模型的性能。

此外，代码还包括了一些常用的PyTorch操作，如将模型放到GPU上，将数据放到GPU上等。

import torch
import torch.nn.functional as F
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

# 1、准备数据集
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
train_dataset = datasets.MNIST(root='../P6 逻辑斯谛回归/data', train=True, download=False, transform=transform)
test_dataset = datasets.MNIST(root='../P6 逻辑斯谛回归/data', train=False, download=False, transform=transform)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)  # 测试集设置为False，方便观察结果


# 2、设计模型
# 2.1 残差块
class ResidualBlock(torch.nn.Module):
    def __init__(self, channels):
        super(ResidualBlock, self).__init__()
        self.channels = channels
        # 定义两个卷积层,卷积核大小为3，padding=1保证输入输出大小一致,输入输出通道数一致，目的保证维度一致，能将输入与输出相加
        self.conv1 = torch.nn.Conv2d(channels, channels, kernel_size=3, padding=1)
        self.conv2 = torch.nn.Conv2d(channels, channels, kernel_size=3, padding=1)

    def forward(self, x):
        y = F.relu(self.conv1(x))  # 第一个卷积层+激活函数
        y = self.conv2(y)  # 第二个卷积层+激活函数
        return F.relu(x + y)  # 将输入与输出相加，再经过激活函数


# 2.2 设计网络
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 卷积层
        self.conv1 = torch.nn.Conv2d(1, 16, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(16, 32, kernel_size=5)

        # 残差块
        self.res1 = ResidualBlock(16)
        self.res2 = ResidualBlock(32)

        self.mp = torch.nn.MaxPool2d(2)  # 最大池化层
        self.l1 = torch.nn.Linear(512, 10)  # 全连接层,不确定第一个参数为多少时，可以先随便写一个，然后运行程序，看报错信息

    def forward(self, x):
        # Flatten data from (n, 1, 28, 28) to (n, 784)
        batch_size = x.size(0)  #获取batch_size,这里的batch_size=64
        x = self.mp(F.relu(self.conv1(x)))  # 经过第一个卷积层+激活函数+池化层
        x = self.res1(x)  #经过第一个残差块处理
        x = self.mp(F.relu(self.conv2(x)))  # 经过第二个卷积层+激活函数+池化层
        x = self.res2(x)  #经过第二个Inception块处理
        x = x.view(batch_size, -1)  # 将数据展平，方便全连接层处理
        x = self.l1(x)  # 全连接层
        return x


model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")  # 判断是否有GPU加速
model.to(device)  # 将模型放到GPU上

# 3、构建损失和优化器
criterion = torch.nn.CrossEntropyLoss()  # 交叉熵损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 优化器,lr为学习率，momentum为动量


# 4、训练和测试
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, labels = data
        inputs, labels = inputs.to(device), labels.to(device)  # 将数据放到GPU上
        optimizer.zero_grad()  # 梯度清零
        # forward + backward + update
        outputs = model(inputs)  # outputs并不是概率，而是线性层的输出，但其大小顺序与概率分布相同
        loss = criterion(outputs, labels)
        loss.backward()  # 反向传播
        optimizer.step()  # 更新参数

        running_loss += loss.item()
        if batch_idx % 300 == 299:  # 每300个batch打印一次平均loss
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0
    total = 0
    with torch.no_grad():  # 测试过程中不需要计算梯度
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)  # 将数据放到GPU上
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)  # 返回每一行中最大值的那个元素，以及其索引
            total += labels.size(0)  # labels的size为[64]，即64个样本
            correct += (predicted == labels).sum().item()  # 统计预测正确的样本个数
    accuracy = 100 * correct / total
    accuracy_list.append(accuracy)
    print('Accuracy on test set: %d %%' % accuracy)


if __name__ == '__main__':
    accuracy_list = []
    for epoch in range(10):
        train(epoch)
        test()
    plt.plot(accuracy_list)
    plt.xlabel('epoch')
    plt.ylabel('accuracy')
    plt.grid()
    plt.show()

[1,   300] loss: 0.525
[1,   600] loss: 0.151
[1,   900] loss: 0.108
Accuracy on test set: 97 %
[2,   300] loss: 0.093
[2,   600] loss: 0.069
[2,   900] loss: 0.074
Accuracy on test set: 98 %
[3,   300] loss: 0.063
[3,   600] loss: 0.060
[3,   900] loss: 0.055
Accuracy on test set: 98 %
[4,   300] loss: 0.050
[4,   600] loss: 0.049
[4,   900] loss: 0.044
Accuracy on test set: 98 %
[5,   300] loss: 0.043
[5,   600] loss: 0.036
[5,   900] loss: 0.043
Accuracy on test set: 98 %
[6,   300] loss: 0.035
[6,   600] loss: 0.034
[6,   900] loss: 0.036
Accuracy on test set: 98 %
[7,   300] loss: 0.031
[7,   600] loss: 0.032
[7,   900] loss: 0.032
Accuracy on test set: 99 %
[8,   300] loss: 0.027
[8,   600] loss: 0.029
[8,   900] loss: 0.029
Accuracy on test set: 99 %
[9,   300] loss: 0.023
[9,   600] loss: 0.025
[9,   900] loss: 0.028
Accuracy on test set: 99 %
[10,   300] loss: 0.024
[10,   600] loss: 0.021
[10,   900] loss: 0.023
Accuracy on test set: 98 %

使用Residual Network后发现准确率确实很快就上升到了99%，但后面有下降的趋势，会一直下降吗？

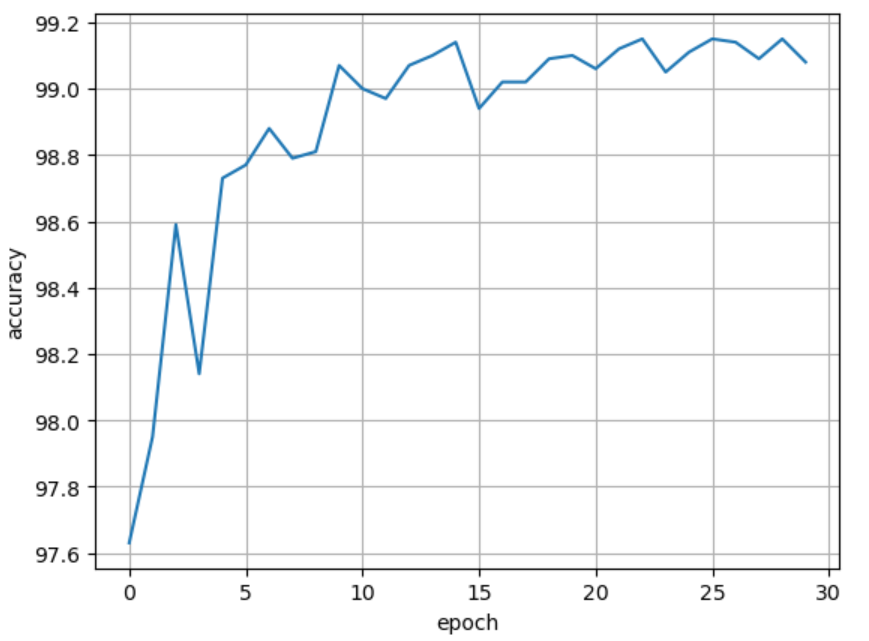
将epoch增大到30时，结果如下图：在epoch大于15时，模型效果还是能够稳定超过99%，说明上图的下降趋势只是虚晃一枪。