0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖，由本人亲自从底层编写、测试与文章配套的各个经典算法，不依赖于现有库，可以大大加深对算法的理解。

?详情：机器学习强基计划(附几十种经典模型源码)

1 Bagging框架

并行集成学习通过并行地训练多个基础模型，并将它们的预测结果进行集成，以提高整体的学习性能和泛化能力。

在并行集成学习算法中，首先需要构建一个包含多个基础模型的集合。这些基础模型可以使用不同的学习算法或具有不同的参数设置。然后，训练数据会被分成多个子集，每个子集用于训练一个基础模型。在并行训练过程中，每个基础模型都独立地学习数据，并生成预测结果。这些预测结果可以通过投票、平均值或加权平均等方式进行集成。最终的集成结果被视为最终预测结果。

自助引导聚合算法(bootstrap aggregating, Bagging)是并行集成学习最著名的代表，核心原理为：基于自助采样法采样出$T$个容量为$m$的样本子集，利用样本子集训练$T$个个体学习器，由于每个样本子集包含63.2%的样本，因此学习器性能不至于太差。对自助采样法不熟悉的同学请看：机器学习强基计划0-3：数据集核心知识串讲，构造方法解析

同时每个子集未覆盖36.8%的样本，造成学习器间的差异性；最后Bagging算法通常采用简单投票法或简单平均法进行集成。

Bagging算法集成原理非常简单，但优势明显：

• Bagging的复杂度与个体学习算法同阶，且各学习器训练过程可并行独立化，计算效率高；
• Bagging可以不经修改直接应用于多分类、回归任务；
• Bagging集成的每个学习器都有36.8%的未使用样本可用于包外估计(out-of-bag estimate)，包外样本可以作为验证集辅助模型的参数优化。

2 Bagging算法实现

Bagging算法基本流程如表所示

核心代码如下：

def predict(self, data):
    label = set(self.data.iloc[:, -1])
    predictLabels = []

    for i in range(data.shape[0]):
        res = np.array([self.base[t].predict(data.iloc[i], self.base[t].tree) for t in range(self.T)])
        resDict = {_label:len(res[res==_label]) for _label in label}
        predictLabels.append(max(resDict.items(), key=lambda x:x[1])[0])
    return np.array(predictLabels)
  
def __bootstrap(self):
    return self.data.sample(n=self.m, replace=True)

其分类效果如下所示

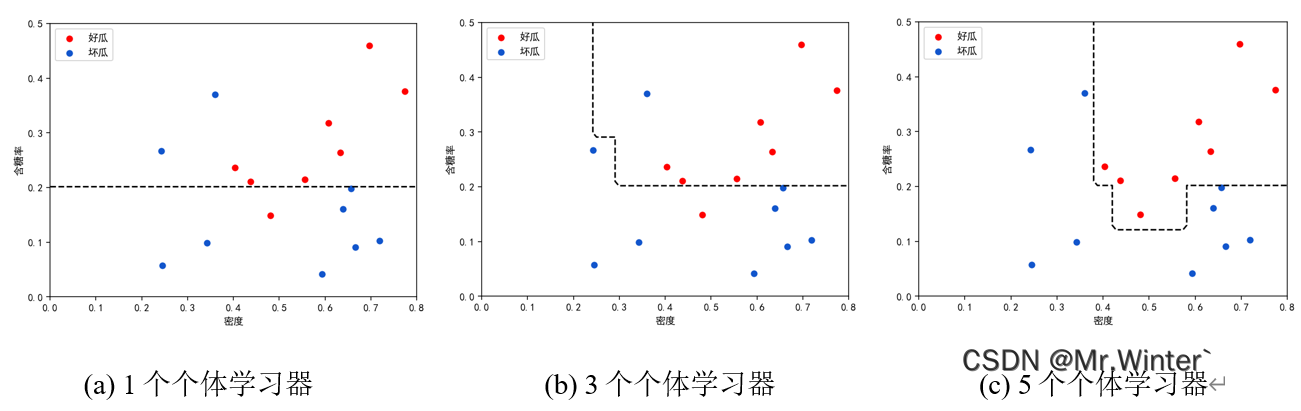
3 随机森林原理与实现

随机森林(Random Forest, RF)是Bagging的一个以决策树为基学习器的扩展变体。具有简单易实现、计算开销小且泛化能力强大的优势。

具体地，随机森林中基决策树的每个节点可选属性子集随机选择自全属性集(假设有$d$个属性)，子集容量$k$控制了随机程度。特别地，当$k=d$时基决策树等效为传统决策树。一般地，推荐$k={\log }_{2}d$。

与Bagging相比，随机森林中的多样性不仅来自自助法的样本扰动，还来自属性扰动，这使得最终集成的泛化性能可通过个体学习器之间差异度的增加而进一步提升。

核心代码如下

def train(self):
   self.base = []
   for i in range(self.T):
       model = DT(self.__bootstrap())
       model.generateTree(model.calGainInfo, layer=None)
       self.base.append(model)
   
def __bootstrap(self):
   attr = np.random.choice(self.d, self.k, replace=False)
   attr = np.append(attr, self.d)
   data = self.data.iloc[:, attr]
   return data.sample(n=self.m, replace=True)

采用西瓜数据集做一个简单的测试

# 训练集数据
csvTrainPath = os.path.abspath(os.path.join(__file__, "../data/dataset3.0train.csv"))
trainSet = preProcessData(
            loadCsvData(csvTrainPath,
            ["色泽", "根蒂", "敲声", "纹理", "脐部", "触感", "密度", "含糖率", "好瓜"], 'df'))

# 验证集数据
csvValidPath = os.path.abspath(os.path.join(__file__, "../data/dataset3.0valid.csv"))
validSet = preProcessData(
            loadCsvData(csvValidPath,
            ["色泽", "根蒂", "敲声", "纹理", "脐部", "触感", "密度", "含糖率", "好瓜"], 'df'))

# 训练集成模型
model = RandomForest(trainSet, T=9)
model.train()
predictLabels = model.predict(validSet)

# 计算准确率
right, num = 0, validSet.shape[0]
for i in range(num):
    if predictLabels[i] == validSet.iloc[i, -1]:
        right = right + 1
acc = right / num
print("准确率为:{:.2f}".format(acc))

可以得到结果

>>> 准确率为:1.00

完整代码通过下方名片联系博主获取

? 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …