题目内容

小蓝有一个神奇的炉子用于将普通金属 O 冶炼成为一种特殊金属 X 。

这个炉子有一个称作转换率的属性 V ，V 是一个正整数，这意味着消耗 V 个普通金属 O
恰好可以冶炼出一个特殊金属 X ，当普通金属 O 的数目不足 V 时，无法继续冶炼。

现在给出了 N 条冶炼记录，每条记录中包含两个整数 A 和 B ，这表示本次投入了 A 个普通金属 O ，最终冶炼出了 B 个特殊金属 X 。

每条记录都是独立的，这意味着上一次没消耗完的普通金属 O 不会累加到下一次的冶炼当中。

根据这 N 条冶炼记录，请你推测出转换率 V 的最小值和最大值分别可能是多少，题目保证评测数据不存在无解的情况。

输入格式

第一行一个整数 N ，表示冶炼记录的数目。

接下来输入 N 行，每行两个整数 A、B ，含义如题目所述。

输出格式

输出两个整数，分别表示 V 可能的最小值和最大值，中间用空格分开。

数据范围

对于 $30\%$ 的评测用例，$1\le N\le 10^2$。
对于 $60\%$ 的评测用例，$1\le N\le 10^3$。
对于 $100\%$ 的评测用例，$1\le N\le 10^4，1\le B\le A\le 10^9$。

输入样例：

3
75 3
53 2
59 2

输出样例：

20 25

样例解释
当 $V=20$ 时，有：$\lfloor \frac{75}{20}\rfloor =3，\lfloor \frac{53}{20}\rfloor =2，\lfloor \frac{59}{20}\rfloor =2$，可以看到符合所有冶炼记录。

当 $V=25$ 时，有：$\lfloor \frac{75}{25}\rfloor =3，\lfloor \frac{53}{25}\rfloor =2，\lfloor \frac{59}{25}\rfloor =2$，可以看到符合所有冶炼记录。

且再也找不到比 20 更小或者比 25 更大的符合条件的 V 值了。

二分法

解析

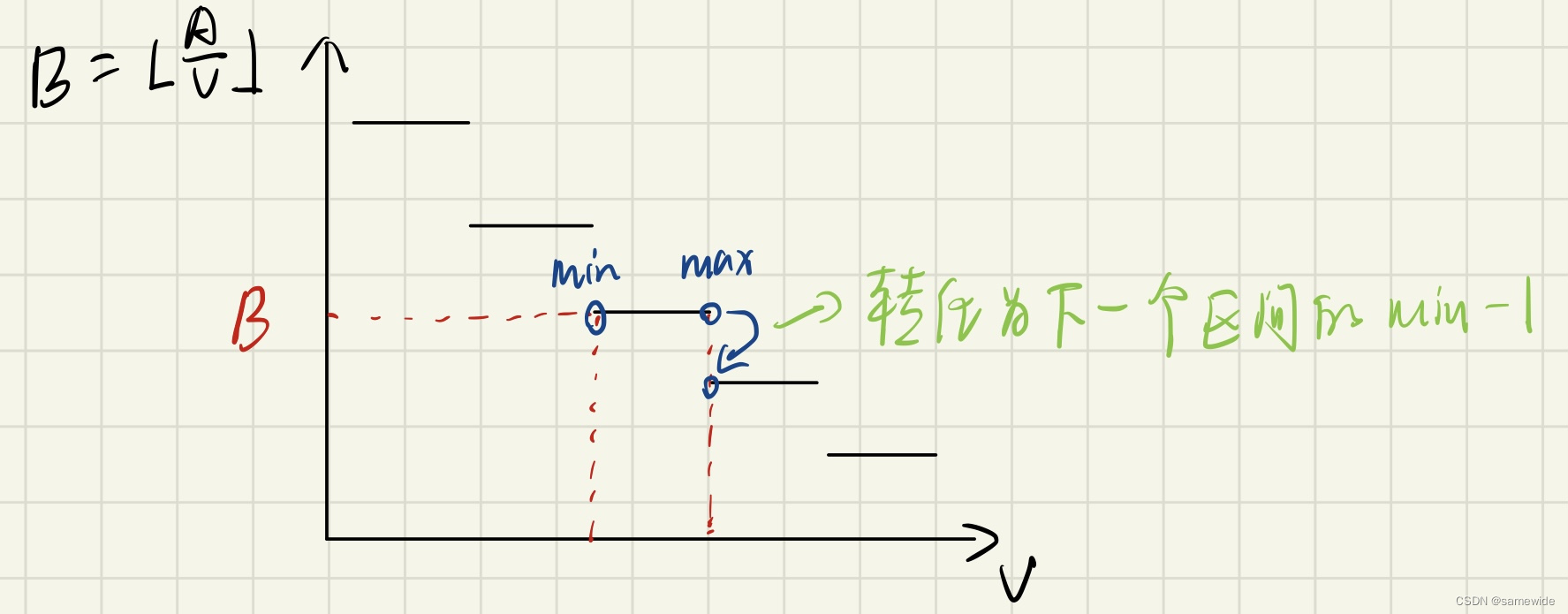
我们可以把$\lfloor \frac{A}{V}\rfloor =B$看成一个函数，把$V$当作自变量，$B$当作因变量，容易知道，这是一个反比例函数的形状，但是由于下取整，所以实际上以一个下降的分段函数
满足条件的v一定是在一段区间上，则满足这一条记录的v的最小值即为这段区间的左端点。分析到这里，这道题目的单调性就被发现了，我们这时采用二分查找即可找到min，再取所有记录的min中最大的一个，即为整体的min
对于max，由于它位于区间的右端点，我们也可以重新写一个二分查找去寻找右端点，但代码量增加，可以采取一个转化，仍然使用同一个二分查找的函数。我们寻找满足B + 1的下一个区间的左端点，此时找到的是满足$\lfloor \frac{A}{V^{\prime }}\rfloor =B-1$，其中可以发现这样的操作会使得$V^{\prime }=V+1$，因此返回的端点-1即可，最后取所有记录中最小的一个，即为整体的max

代码

要注意二分查找中l和r的初始化取值

#include <bits/stdc++.h>

using namespace std;

int binary_search(int a, int b)
{
    int l = 1, r = 2e9 + 1; //由于b存在等于0的情况，也就是说当a = 2e9，b = 0的时候，
    //v必须能取到比a还大的数字，因此要加一
    while(l < r)
    {
        int mid = (l + r) >> 1;
        if(a / mid <= b) r = mid; //这里和正常的二分查找是相反的，因为查找的数字在分母上
        else l = mid + 1;
    }
    return l;
}

int main()
{
    int n;
    cin >> n;
    int v_max = 1e9, v_min = 1; //当A取最大，B取最小的时候可得到最大值1e9，相等的时候取最小值1
    while(n --)
    {
        int a, b;
        scanf("%d %d", &a, &b);
        v_max = min(v_max, binary_search(a, b - 1) - 1); //这里是转化为下一个区间的左端点-1
        v_min = max(v_min, binary_search(a, b));
    }
    
    printf("%d %d", v_min, v_max);
    return 0;
}

公式法

解析

首先我们先列出题目中要求的公式
$$\lfloor \frac{A}{V}\rfloor =B$$
根据下取整的性质，我们有
$$\lfloor \frac{A}{V}\rfloor +1=B+1>\frac{A}{V}\ge \lfloor \frac{A}{V}\rfloor =B$$
进行不等式的简单变换得到
$$\frac{A}{B}\ge V>\frac{A}{B+1}$$
到这里结果就非常明显了，我们只需要寻找$\lfloor \frac{A}{B}\rfloor$的最小值作为max，由于V是整数，所以min一定是大于$\frac{A}{B+1}$的最小整数，当$\frac{A}{B+1}$是整数的时候，直接取$\frac{A}{B+1}+1$即可，如果不是整数，则取$\lfloor \frac{A}{B+1}\rfloor +1$，在C++中这两种操作可以合并。

代码

#include <bits/stdc++.h>

using namespace std;

int n;

int main()
{
    cin >> n;
    int maxs = 0x3f3f3f3f, mins = 0;
    for(int i = 0; i < n; i ++)
    {
        int a, b;
        scanf("%d %d", &a, &b);
        maxs = min(maxs, a / b);
        mins = max(mins, a / (b + 1) + 1); //这里是合并的操作
    }
    
    printf("%d %d", mins, maxs);
    return 0;
}