您现在的位置是:首页 >技术杂谈 >系列文章 之 一文纵览【机器学习】算法(3):线性回归/多项式回归 | 正则化 | 逻辑回归 | 支持向量机SVM | 核方法 | 朴素贝叶斯 | 随机森林 | 神经网络 | KNN(附实例代码)网站首页技术杂谈
系列文章 之 一文纵览【机器学习】算法(3):线性回归/多项式回归 | 正则化 | 逻辑回归 | 支持向量机SVM | 核方法 | 朴素贝叶斯 | 随机森林 | 神经网络 | KNN(附实例代码)
最近看到两段话,希望对所处境地不是很理想的朋友有些帮助,特此分享给大家:
【1】生活可能不像你想象的那么好,但是也不会像你想象的那么糟,人的脆弱和坚强都超乎了自己的想象,有时候脆弱的一句话会让你泪流满面,有时候你发现自己咬着牙已经走过了很长的路。
【2】世界上的事情,最忌讳的就是个十全十美,你看那天上的太阳,一旦圆满了,马上就要亏厌;树上的果子,一旦熟透了,马上就要坠落。凡事总要稍留欠缺,才能持恒。
?作者主页: 追光者♂?
?个人简介:
?[1] 计算机专业硕士研究生?
?[2] 2022年度博客之星人工智能领域TOP4?
?[3] 阿里云社区特邀专家博主?
?[4] CSDN-人工智能领域优质创作者?
?[5] 预期2023年10月份 · 准CSDN博客专家?
- 无限进步,一起追光!!!
?感谢大家 点赞? 收藏⭐ 留言?!!!
此前曾分享:
- 系列文章 之 一文纵览【机器学习】必备步骤(2),祝(助)你(我们) 科研/实验 不再踌躇 | 附:16个必会Python内置数据转换计算函数(1)
- 系列文章 之 一文纵览【机器学习】必备步骤(1),祝(助)你(我们) 科研/实验 不再踌躇
?该系列文章主打简单实用!用尽可能通俗的语言,带读者入门机器学习算法。附带易理解的纯干货代码,让初学者也能对机器学习有更好的理解!涉及到的机器学习基础算法有:线性回归(含多项式回归)、正则化、逻辑回归、支持向量机、核方法、朴素贝叶斯、随机森林、神经网络、KNN等基础的 9个有监督机器学习算法。该系列将持续更新!
本篇介绍的知识属于机器学习的基础算法,简单易懂。已经学习过的朋友在看到概念时可以选择性跳过哦~
?目录
?一、Linear Regression(算法一)
?1.1 简介、斜率、截距、学习参数
众所周知,Linear Regression 即 线性回归。它是用于预测回归问题的算法,其中,根据训练数据计算使损失最小的参数的做法是有监督学习算法的共同之处。
线性回归 是对“目标变量”随着某个特征变量的增大而增大(或者“减小”)这种关联性建模的方法。
对于直线 y = w 0 + w 1 x y=w_0+w_1x y=w0+w1x,这是我们在中学阶段学习过的一次函数。 w 1 w_1 w1是斜率(或者叫做 权重), w 0 w_0 w0相当于在y轴上的截距。
斜率 w 1 w_1 w1 和 截距 w 0 w_0 w0 是由有监督学习的算法学习到的参数,因此我们称之为学习参数。
线性回归算法一般使用一个以上的特征变量创建模型,其中只有一个独立的特征变量的情况叫做一元回归。
(该算法我此前已讲解过多次,这里主要用来为初学者复习使用)
?1.2 示例 code
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 9:24
from sklearn.linear_model import LinearRegression
X = [[10.0], [8.0], [13.0], [9.0], [11.0], [14.0], [6.0], [4.0], [12.0], [7.0], [5.0]]
y = [8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68]
model = LinearRegression()
model.fit(X, y)
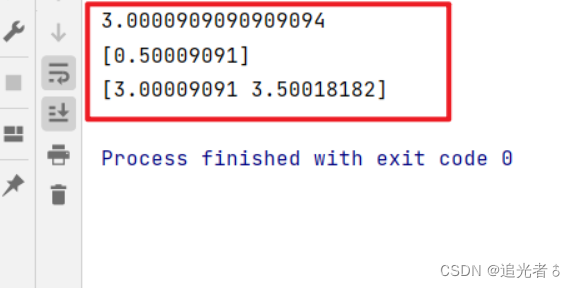
print(model.intercept_) # 截距
print(model.coef_) # 斜率
y_pred = model.predict([[0], [1]])
print(y_pred) # 对x=0, x=1的预测结果
这里直接从sklearn库中导入线性回归模型,我们自定义一些数据,包含自变量 x x x和因变量 y y y,用简单线性回归来拟合。实用fit()方法来训练。并打印截距、斜率,此后再进行预测。
?1.3 线性回归 与 非线性回归
这个小节主要练习一元回归。一元回归 是指独立特征变量只有一个时的线性回归,独立特征变量为两个及以上时的线性回归叫做多元回归。
另外,尽管独立特征变量只有一个,但包含 x 2 x^2 x2、 x 3 x^3 x3这种特征变量的次方项的线性回归叫做 多项式回归。
多项式回归对于特征变量
x
i
x_i
xi不是线性的,因此把它叫做“线性”回归
就好像感觉不是很合适。
但事实上,是否为线性回归不是从特征变量来看的。从学习参数 (本例中是 x 1 2 x^2_1 x12和 x 1 x_1 x1的系数) 的角度来看是线性的回归,我们才成为线性回归,所以多项式回归也属于线性回归。
各种线性回归的例子:
| 线性回归的种类 | 示例 |
|---|---|
| 一元回归 | y = w 0 + w 1 x 1 y = w_0+w_1x_1 y=w0+w1x1 |
| 多元回归 | y = w 0 + w 1 x 1 + w 2 x 2 y=w_0+w_1x_1+w_2x_2 y=w0+w1x1+w2x2 |
| 多项式回归 | y = w 0 + w 1 x 1 + w 2 x 1 2 y=w_0+w_1x_1+w_2x^2_1 y=w0+w1x1+w2x12 |
?二、 正则化(算法二)
?2.1 简介
正则化是防止过拟合的一种方法,常与线性回归等算法配合使用。可通过向损失函数增加惩罚项的方式对模型施加制约(正则化可以抑制模型的复杂度),它有望提高模型的泛化能力。
正则化用于机器学习模型的训练阶段。
我们知道,过拟合是模型在验证数据上产生的误差(训练误差)大得多的现象,过拟合的一个原因是机器学习模型过于复杂。而正则化可以降低模型的复杂度,有助于提高模型的泛化能力。
现在已经有许多正则化的方法,岭回归 是一种很常见的回归模型。下面我们对sin函数进行岭回归建模。(使用PolynomialFeatures方法创建六次多项式)
?2.2 示例 code
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 9:53
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
train_size = 20
test_size = 12
train_X = np.random.uniform(low=0, high=1.2, size=train_size)
test_X = np.random.uniform(low=0.1, high=1.3, size=test_size)
train_y = np.sin(train_X * 2 * np.pi) + np.random.normal(0, 0.2, train_size)
test_y = np.sin(test_X * 2 * np.pi) + np.random.normal(0, 0.2, test_size)
poly = PolynomialFeatures(6) # 次数为6
train_poly_X = poly.fit_transform(train_X.reshape(train_size, 1))
test_poly_X = poly.fit_transform(test_X.reshape(test_size, 1))
model = Ridge(alpha=1.0)
model.fit(train_poly_X, train_y)
train_pred_y = model.predict(train_poly_X)
test_pred_y = model.predict(test_poly_X)
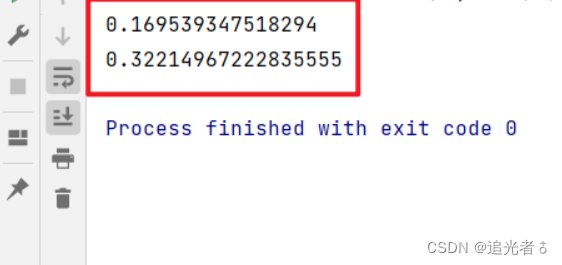
print(mean_squared_error(train_pred_y, train_y))
print(mean_squared_error(test_pred_y, test_y))
?三、逻辑回归(算法三)
?3.1 简介
逻辑回归是一种用于有监督学习的分类任务的简单算法,虽然算法的名字中包含“回归”二字,但其实它是用于分类问题的算法。逻辑回归通过计算数据属于各类别的概率来进行分类。
上面提到,逻辑回归是一种学习某个事件发生概率的算法。利用这个概率,可以对某个事件发生或不发生进行二元分类。
虽然逻辑回归本来是二元分类的算法,但也可以用于三种类别以上的分类问题。
逻辑回归 可根据数据 x x x 和表示其所属类别的标签 y y y 进行学习,计算概率。数据 x x x 可以当做由特征值组成的向量处理。如果标签是二元分类,则可以使用 y = 0 , 1 y=0,1 y=0,1 这种二元数值表示。
逻辑回归的基本思想与线性回归一样,对数据 x x x乘以权重向量 w w w,再加上偏置 w 0 w_0 w0,计算 w T x + w 0 w^Tx+w_0 wTx+w0的值。逻辑回归和线性回归在从数据中学习权重 w w w和偏置 w 0 w_0 w0这一点上是相同的。
而与线性回归不同的是,为了计算概率,逻辑回归的输出范围必须限制在0和1之间。逻辑回归使用Sigmoid函数 σ ( z ) = 1 / [ 1 + e x p ( − z ) ] sigma(z)=1/[1+exp(-z)] σ(z)=1/[1+exp(−z)],返回0和1之间的数值。
-
亦可回顾:建议收藏【机器学习&练习 θ】逻辑回归(详细分析:数据可视化、sigmoid 函数、代价函数和梯度、评价 逻辑回归模型 等知识…)
-
【概念】详细介绍:什么是BP神经网络?(Sigmoid 激活函数,再次介绍) || 感受野 || 前向传播 和 反向传播
-
(包括但不限于上述文章~)
决策边界:
在解决分类问题时,如果让学习后的模型对未知数据分类,模型就会以某个地方为边界来区分分类结果,这个边界就叫做决策边界。逻辑回归的决策边界是计算出的概率正好为50%的地方。
决策边界的形状因使用的算法不同而有很大的不同。在平面的情况下,逻辑回归的决策边界是直线。在其他算法中,例如KNN和神经网络,决策边界将会是更复杂的形式。这些内容我都曾介绍过。
?3.2 示例 code
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 10:20
import numpy as np
from sklearn.linear_model import LogisticRegression
X_train = np.r_[np.random.normal(3, 1, size=50), np.random.normal(-1, 1, size=50)].reshape((100, -1))
y_train = np.r_[np.ones(50), np.zeros(50)]
model = LogisticRegression()
model.fit(X_train, y_train)
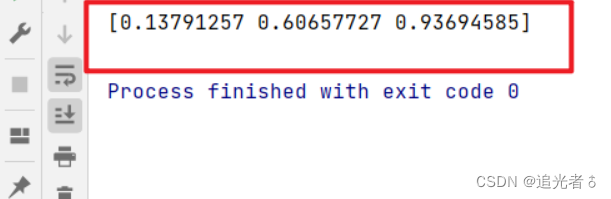
print(model.predict_proba([[0], [1], [2]])[:, 1])
?四、支持向量机SVM(算法四)
?4.1 简介
支持向量机,Support Vector Machine,SVM,这是一种应用范围非常广泛的算法,既可以用于分类,也可以用于回归。
我们这里以线性支持向量机为例。线性SVM是以间隔最大化为基准,来学习得到尽可能地远离数据的决策边界的算法。虽然该算法的决策边界与逻辑回归一样是线性的,但有时线性SVM得到的效果更好。
上面提到“间隔最大化”。那么什么是间隔?
为方便起见,我们以平面上的二元分类问题为例进行说明,并且假设数据可以完全分类。线性SVM通过线性的决策边界将平面一分为二,据此进行二元分类。此时,训练数据中最接近决策边界的数据与决策边界之间的距离就称为间隔。
?4.2 示例 code
下面我们生成线性可分的数据,将其分割成训练数据和验证数据,使用训练数据训练线性SVM,使用验证数据评估正确率。此外,由于使用了随机数,因此每次运行的结果大概率会有所不同。
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 10:37
from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 数据生成
centers = [(-1, -0.125), (0.5, 0.5)]
X, y = make_blobs(n_samples=50, n_features=2, centers=centers, cluster_std=0.3)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = LinearSVC()
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
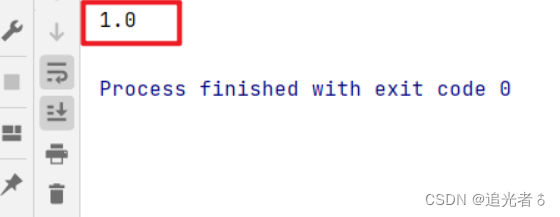
print(accuracy_score(y_pred, y_test)) # 评估
?五、支持向量机(核方法)【算法五】
?5.1 简介
在深度学习出现之前,使用核方法的支持向量机很受欢迎!
通过在支持向量机中引入 核方法(kernel methods) (使得模型可以学习复杂的决策边界)这个技巧,那些无法人力标注特征值的复杂数据也能被处理。当然,该算法现在也用于解决各种分类和回归问题。
众所周知,线性支持向量机通过最大化间隔,可以得到尽可能远离数据的“好的”决策边界。但是由于决策边界必定为直线,所以它很难对“每个标签的边界为曲线的数据”进行分类。
也就是说,模型需要学习曲线的线性决策边界、SVM可以使用&方法学习复杂的决策边界。
核方法的一个较为普遍的解释是:“将数据移动到一个特征空间,然后进行线性回归”。
对于该解释的理解。我们首先思考一下如何使线性不可分数据成为线性可分数据。假设有一个比训练数据更高维的空间,训练数据中的每一个点都对应着这个高维空间中的一个点。在这个高维空间中,训练数据对应的点是可以线性分离的,实际的训练数据是来自于该高维空间的投影。一旦有了这样的空间,模型就可以在高维空间中使用SVM来学习决策边界。最后,将高维空间的决策边界投影到由原始特征形成的向量空间上,得到决策边界。
?5.2 示例 code
通过示例代码来看一下使用核方法的SVM如何学习呈圆形分布的数据的决策边界。
我们生成呈圆形分布的数据,将其拆分成训练数据和验证数据,使用训练数据训练模型,使用验证数据评估正确率。
我在代码中没有明确指定使用哪个核方法,这是因为代码默认使用RBF(Radial Basis Function。径向基函数)核方法。
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 15:53
from sklearn.svm import SVC
from sklearn.datasets import make_gaussian_quantiles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 数据生成
X, y = make_gaussian_quantiles(n_features=2, n_classes=2, n_samples=300)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = SVC()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(accuracy_score(y_pred, y_test))
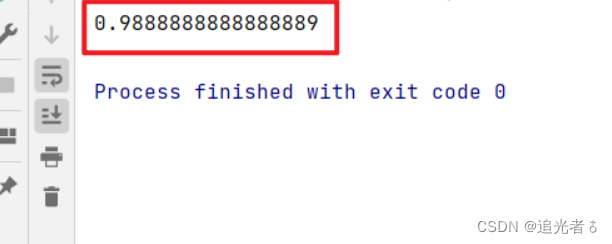
?5.3 其它说明
核方法中可以使用的核函数多种多样。使用不同的核函数,得到的决策边界也不同。
一些常见的函数有:线性核函数、Sigmoid核函数、多项式核函数、RBF核函数等等。
注意:使用核方法后,我们就无法清楚地知道SVM使用的是什么特征了。核方法适用于“相比特征的可解释性更看重精度”的场景。需要指出的是,得到的决策边界不一定是通过示例code学习到的那种一目了然的决策边界。
由于这些特点,在使用SVM时,不宜立即使用非线性核函数,在此之前,应先使用线性核函数进行分析,以了解数据。
?六、朴素贝叶斯(算法六)
?6.1 简介
朴素贝叶斯(Naive Bayes)是常用于自然语言分类问题的算法。它在垃圾邮件过滤上的应用是非常有名的!
朴素贝叶斯是一个基于概率进行预测的算法,在实践中被用于分类问题。具体来说,就是计算数据为某个标签的概率,并将其分类为概率值最大的标签。朴素贝叶斯主要用于文本分类和垃圾邮件判定等自然语言处理中的分类问题。
虽然最终要做的是自然语言处理的分类,但在应用朴素贝叶斯时,还需要将输入数据转换为由特征值构成的向量。我们先在预处理阶段将文本转换为由特征值构成的向量,然后使用朴素贝叶斯进行训练,最后查看结果。
例如,朴素贝叶斯使用训练数据来学习与各标签对应的单词的概率。在分类时求出每个标签对应的概率,将概率最高的标签作为分类结果。朴素贝叶斯在训练时计算以下两种概率。
- 1、每个标签出现的概率;
- 2、在各标签下,每个单词出现的概率。
?6.2 示例 code
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 16:24
from sklearn.naive_bayes import MultinomialNB
# 数据生成
X_train = [[1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1]]
y_train = [1, 1, 1, 0, 0, 0]
model = MultinomialNB()
model.fit(X_train, y_train) # 训练
print(model.predict([[1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0]])) # 评估
此处输出的array[1],意为着一种类别。

?6.3 补充说明
注意:朴素贝叶斯是自然语言分类的基础算法,但是不适合预测天气预报中的降水概率那种预测值本身是概率的情况。假设 朴素贝叶斯基于“每个单词的概率可以独立计算”的假设,这是为了使概率的计算方法尽量简单。这个假设忽略忽略了文本中单词之间的关联性。如果要计算的概率值很重要,那么应该避免直接将由朴素贝叶斯算出的值用作概率。
另外,朴素贝叶斯的“即使将各自的特征作为独立的变量来处理,也可以计算出概率”这一假设对于某些学习任务不成立。例如,如果单词在不同的上下文中含义不同,那么朴素贝叶斯的假设是不成立的。
比如说,“踢”这个单词常常在格斗等运动的文本中出现,但是如果文本中出现了“踢了球”的用法,那么此时文本的主题很有可能是足球。这种单词含义在不同的上下文中有所变化的情况不满足朴素贝叶斯“所有特征都是相互独立的”这一假设的。如果要考虑单词的上下文,就需要根据不同的上下文考虑使用其他模型。
?七、随机森林(算法七)
?7.1 简介
随机森林(random forest)是将多个模型综合起来创建更高性能模型的方法,既可用于回归,也可用于分类。同样的算法有梯度提升(gradient boosting)等在机器学习竞赛中很受欢迎的算法。
(通过学习随机森林,我们可以学到在其他算法中也适用的基础知识)
随机森林的目标是利用多个决策树模型,获得比单个决策树更高的预测精度。单个决策树的性能并不一定很高,但是多个决策树汇总起来,一定能创建出泛化能力更强的模型。
随机森林的多数表决就像是找别人商量事情一样,不只听一个人的意见,而是在听取许多人的意见之后综合判断。机器学习也一样,通过创建多个模型,采取多数表决的方式,可以期待获得更为妥当的结果。
需要注意的是,如果使用同样的学习方法创建决策树,那么输出的就都是同样的东西,也就失去了采取多数表决的意义。在随机森林中,采用的决策树要具备多样性,这是很重要的一点。
决策树:
随机森林是综合决策树的结果的算法。决策树,是通过将训练数据按条件分支进行划分来解决分类问题的方法,在分割时利用了表示数据杂乱程度(或者不均衡程度)的不纯度的数值。决策树为了使表示数据杂乱程度的不纯度变小,对数据进行分割。当分割出来的组中存在很多相同的标签时,不纯度会变小;反之,当分割出来的组中存在很多不同的标签时,不纯度会变大。
(随机森林可以让我们知道每个特征对预测结果的重要度。)
前面讲过,每棵决策树的学习方法都是通过沿着某个值分割特征,使不纯度尽可能地小。通过对随机森林的所有决策树求在以某个特征分割时的不纯度并取平均值,可以得到特征的重要度。将重要度高的特征用于分割,有望大幅度减小不纯度。反之,重要度低的特征即使被用于分割,也无法减小不纯度。所以可以说这样的特征是非必要的。基于特征的重要度,我们可以去除非必要的特征。
?7.2 示例 code
让我们用随机森林基于3种葡萄酒的各种测量值数据。对葡萄酒进行分类。
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 20:13
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 数据生成
data = load_wine()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.3)
model = RandomForestClassifier()
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
print(accuracy_score(y_pred, y_test)) # 评估

?八、神经网络(算法八)
?8.1 简介
一直以来,人们都认为神经网络(Neural Network,NN)是模仿生物体的神经网络设计而成的。
神经网络即可以用于回归,也可以用于分类,但在实际应用中常用于分类。 基于神经网络的深度学习因在图像识别和语音识别等领域表现优异而广为人知。
神经网络在输入数据和输出结果之间插入了叫做中间层的层,能够学习复杂的决策边界。(只由输入层和输出层可以构成简单的感知机,简单感知机是将非线性函数应用于对特征值加权后的结果并进行识别的模型。简单感知机与逻辑回归具有类似的特性,其实在用Sigmoid函数作为激活函数 f f f时,简单感知机与逻辑回归是等价的)通过叠加简单感知机,神经网络得以表示复杂的决策边界。 (简单感知机不能很好地学习某些数据的决策边界,逻辑回归无法成功地对非线性决策边界进行分类)
神经网络通过设置中间层的方式,可以利用单一算法学习各种决策边界。通过调节中间层的数量以及层的深度,神经网络可以学习更复杂的边界。
?8.2 示例
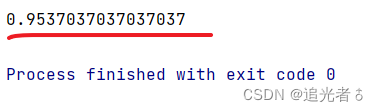
下面读取MNIST数据集,将其分割成训练数据和验证数据,使用训练数据训练模型,使用验证数据评估正确率。每次运行结果都有所不同,不过结果的正确率都在95%左右。
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 20:38
from sklearn.datasets import load_digits
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 数据生成
data = load_digits()
X = data.images.reshape(len(data.images), -1)
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = model = MLPClassifier(hidden_layer_sizes=(16,))
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
print(accuracy_score(y_pred, y_test)) # 评估
?九、KNN(算法九)
?9.1 简介
KNN(K-Nearest Neighbor,K近邻)算法是一种与众不同的机器学习算法,它只是机械地基础所有的数据。KNN的历史悠久,早已为人所知,不过,该算法虽然简单,却可以学习复杂的边界。
KNN既可用于分类,也可用于回归。KNN在训练时机械地记住所有的训练数据。相较于其他算法要经历“根据训练数据计算最佳参数”的训练阶段和“使用计算出的学习参数进行预测”的预测阶段,KNN在训练阶段不进行任何计算,直到进入预测阶段之后才进行具体的计算。
在对未知数据进行分类时,KNN将计算未知数据与训练数据的距离,通过多数表决找到最邻近的 k k k个点,然后进行分类。
KNN虽然是一种简单的算法,但也适用于具有复杂边界的数据。
该算法使用训练数据对未知输入数据进行分类时的步骤如下。
-
- 计算输入数据与训练数据之间的距离。
-
- 得到距离输入数据最近的 k k k的训练数据。
-
- 对训练数据的标签进行多数表决,将结果作为分类结果。
其中,最近邻点 k k k的数量是一个超参数。在二元分类时,通常取 k k k为奇数,这样多数表决才能决定结果是其中的哪一个。
?9.2 示例 code
我们使用呈曲线分布的样本数据进行学习,从而解决分类问题。最近邻点 k k k的数量采用默认值5。
# 昵 称:XieXu & CSDN@追光者♂
# 时 间: 2023/5/11/0011 20:50
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 数据生成
X, y = make_moons(noise=0.3)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = KNeighborsClassifier()
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
print(accuracy_score(y_pred, y_test)) # 评估
此处报了个小的警告。问题不大,版本所致。

?十、完整code获取
? 热门专栏推荐:
- ?Python&AI专栏:【Python从入门到人工智能】
- ?前端专栏:【前端之梦~代码之美(H5+CSS3+JS.】
- ?论文阅读&项目专栏:【小小的项目 (实战+案例)】
- ?C语言/C++专栏:【C语言、C++基础代码~】
- ?问题解决专栏:【工具、技巧、解决办法】
- ? 加入Community 一起追光:追光者♂社区
持续创作优质好文ing…✍✍✍
记得一键三连哦!!!
求关注!求点赞!求个收藏啦!







 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结