数据结构-线性表-链表网站首页 其他

数据结构-线性表-链表

摘星的晚上、 2024-08-29 00:01:02

简介数据结构-线性表-链表

线性表的链式存储结构：

为了表示数据元素ai和其后继元素ai+1之间的逻辑关系，对ai来说需存储其本身信息和后继元素的信息（存储位置）。这两部分组成ai的存储映像，称为结点（Node），它包含两个域：数据域和指针域。n个结点链结在一起，就组成线性表的链式存储结构。
在这里插入图片描述
1）单向链表

using namespace std;
struct Node
{
	int value;
	Node *next;
}*LinkedList,LNode;

2）双向链表

struct DNode
{
    int value;       /* Data field */
    struct DNode *prior;  /* Pointer field */
    struct DNode *next;   /* Pointer field */
}DNode;

一、单向链表的ADT定义

1.1 创建链表
使用尾插法创建单链表

 //尾插法创建单链表、链表长度为n;
void CreatLinkedList(LinkedList &L,int n)  
{
    L = (LinkedList)malloc(sizeof(LNode));  //初始化;
    L->next = NULL;
    L->data = 0;
    LinkedList Tail = L;    //尾指针;
    cout<<"Enter "<<n<<" number(s)"<<endl;
    for(int i = 0 ; i < n; i++)
    {
        LinkedList Temp = (LinkedList)malloc(sizeof(LNode));
        cin>>Temp->data;
        Tail->next = Temp;
        Tail = Temp;
        Temp = NULL;
        L->data++;  //计数;
    }
    Tail->next = NULL;
}

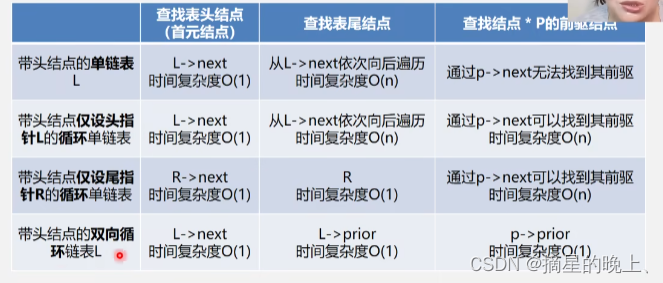
1.2 查找
从头结点开始，逐个查找（后移）并计数，直到第i个为止。
算法的平均时间复杂度为T(n) = O(n)

//查找链表中第一个数据为data的节点，如果找到就返回节点指针，否则返回空指针NULL
Node findInList(LinkedList lst, int data) {
    Node tmp = lst;
    while (tmp->next != NULL) {
        if (tmp->data == data) {
            return tmp;
        }
        tmp = tmp->next;
    }
    return NULL;
}

在这里插入图片描述
1.3 插入
在指定位置插入节点

	// 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addHead(LinkedList* head, int val) {
        LinkedList* newNode = new Node();
        newNode->value = val;
        newNode->next = head->next;
    }

    // 在链表最后面添加一个节点
    void addTail(LinkedList* head, int val) {
        LinkedList* newNode = new Node();
        newNode->value = val;
        newNode->next = nullptr;
        LinkedList* cur = head;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
    }

    // 在链表的某个位置插入一个节点
    void addIndex(LinkedList* head, int index, int val) {
        LinkedNode* newNode = new Node();
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
    }

1.4 删除
删除结点

LinkedList* removeElements(LinkedList* head, int val) {
        //删除头节点
        while((head != NULL)&&(head->value == val)){ 
            Node* temp = head;
            head = head->next;
            delete temp;
        }
        //删除非头节点
        Node*  cur = head;  //头节点不动
        //不是空链表且不是尾部节点
        while((cur != NULL)&&(cur->next != NULL)){
        	//如果下一个节点的值等于目标值，删除
            if(cur->next->val == val){ 
                Node*  temp = cur->next; //
                cur->next = cur->next->next;
                delete temp; 
            }
            else{
                cur = cur->next;
            }
        }
        return head;

1.5 反转链表

    Node* reverseList(ListNode* head) {
    	//初始化一个空指针的节点
        Node* pre = new Node();  
        pre = nullptr;
        ListNode* cur = new Node();
        cur = head;
        Node* temp;
        while(cur != nullptr){
            temp = cur->next; 
            cur->next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }

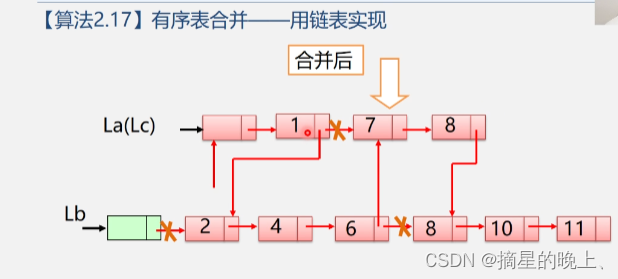
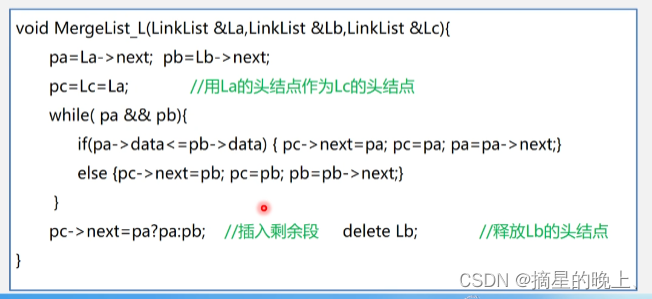
1.6 链表的合并

有序表的合并，用链表实现：
在这里插入图片描述

在这里插入图片描述

Node* mergeList(Node* head1, Node* head2)
	Node* p = head1; // 指向第一个链表的指针
	Node* q = head2; // 指向第二个链表的指针
	Node* dummy = new Node(); // 创建一个虚拟节点
	Node* r = dummy; // 指向新链表的指针
	while (p != nullptr && q != nullptr) {
	    if (p->val < q->val) {
	        r->next = p; // 将第一个链表中的节点插入到新链表中
	        p = p->next; // 移动指针到下一个节点
	    } else {
	        r->next = q; // 将第二个链表中的节点插入到新链表中
	        q = q->next; // 移动指针到下一个节点
	    }
	    r = r->next; // 移动指针到新链表的最后一个节点
	}
	if (p != nullptr) {
	    r->next = p; // 将第一个链表中剩余的节点插入到新链表中
	} else {
	    r->next = q; // 将第二个链表中剩余的节点插入到新链表中
	}
	head = dummy->next; // 将新链表头指针指向第一个节点
	return head;

1.7 链表的长度

int getListSize(LinkedList* head){
	Node* p = head; // 指向链表头节点的指针
	int len = 0; // 链表长度
	while (p != nullptr) {
	    len++;
	    p = p->next; // 移动指针到下一个节点
	}
	cout << "链表的长度为：" << len << endl;
	return len;
}