您现在的位置是：首页 >技术杂谈 >【C++】二叉搜索树网站首页技术杂谈
【C++】二叉搜索树
简介【C++】二叉搜索树
文章目录
二叉搜索树的查找规则
从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
最多查找高度次，走到到空，还没找到，这个值不存在
二叉搜索树(二叉排序树)性质
非空左子树的所有值小于根节点的值非空右子树的所有值大于根节点的值
左右子树都是二叉搜索树
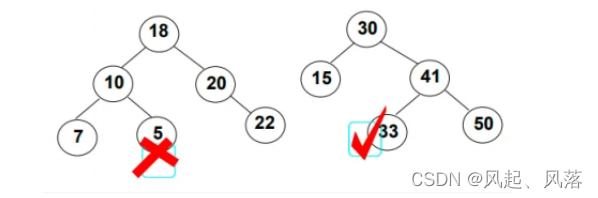
第一个不满足，因为值为5的节点在值为10的节点的右边，正常来说10的右边都应该比10大
二叉搜索树的中序遍历
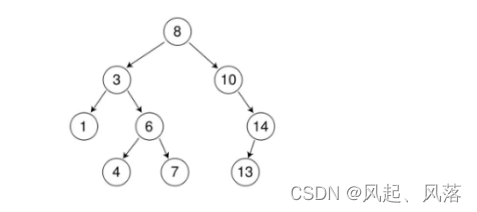二叉搜索树的中序遍历，一定可以得到一个递增的序列 中序为：1 3 4 6 7 8 10 13 14
二叉搜索树的实现 (非递归)
插入
分为两种情况
若插入的值在二叉树中不存在，则通过比较进行插入
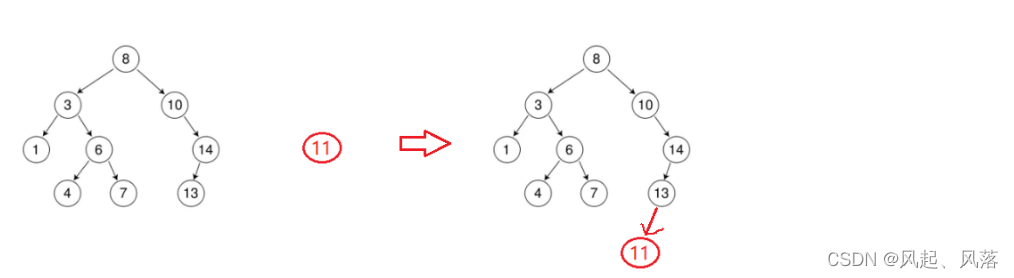
若插入11，因为11比8大，所以跟10比较，而11比10大，所以走10的右子树14，14与11比较，因14>11，所以走14的左子树13，11与13比较，因13>11，故作为13的左子树，遇见NULL指针停止
若插入的值，在二叉树中存在
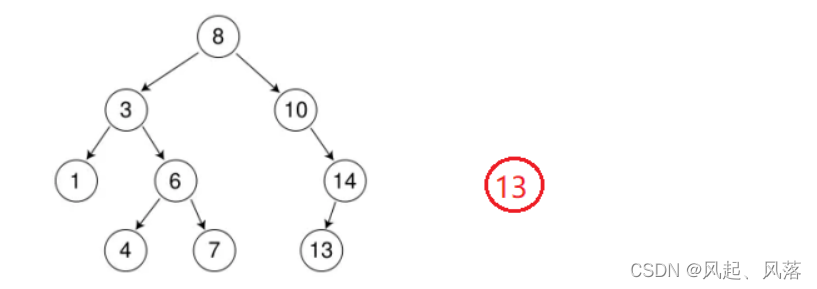
因为插入值13与二叉树中的值13相等，则直接返回false
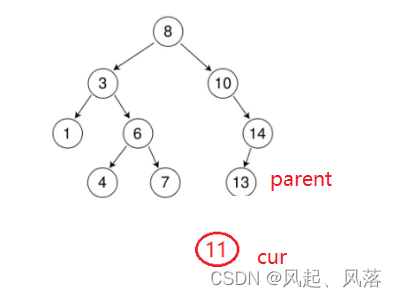
实际上创建节点后，需要与二叉搜索树进行连接，去当前创建节点的上一个节点parent，
通过判断cur节点是parent节点左子树还是右子树 进行连接
bool Insert(const K& key)
{
if (_root = nullptr)//若root根节点为nullptr
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = NULL;//用于接收cur之前的节点
while (cur != NULL)
{
if (cur->_key > key)//若插入的值比cur值小
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)//若插入的值比cur值大
{
parent = cur;
cur = cur->_right;
}
else//若相等，则直接返回false
{
return false;
}
}
//遇见空指针，连接新节点
//由于不知道parent的左还是右连接key，所以需要判断
cur = new Node(key);
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
中序遍历
inorder需要传根，但是由于_root是类的私有成员变量，所以没办法从.c文件传过来
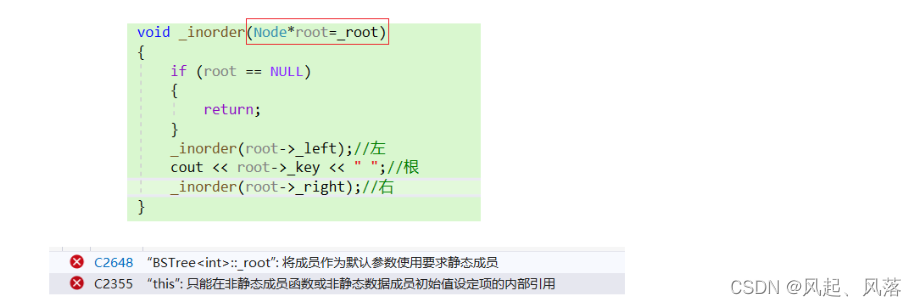
若将inorder函数设为缺省值，不可以通过编译
缺省值必须是常量或者全局变量，而root不是全局变量/常量 ，所以不能用缺省值
访问成员变量需要用this指针，而此时_root并没有this指针去指向
所以采用嵌套一层函数的方式，这样调用inorder函数时，不用传参数过来也可以解决问题
查找
bool Find(const K& key)
{
Node* cur = _root;
while (cur != NULL)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return true;
}
}
return false;
}
删除 (重点)
删除共分为三种情况
1. 要删除节点无孩子节点
删除4后，直接将6的左子树置为NULL
2.要删除节点只有左孩子节点/右孩子节点
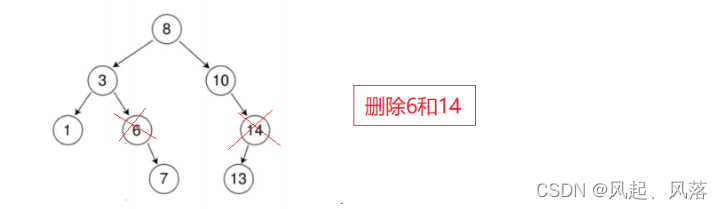
3.要删除节点有左孩子和右孩子节点
删除8节点，就需要寻找左子树的最大节点或者右子树最小节点 来当树的根节点
左子树的最大节点是最右节点
右子树的最小节点是最左节点
假设删除节点8，通过右子树的最小节点来进行替换，将右子树的最小节点替换掉cur节点值，删除右子树的最小节点即可
由于叶子节点的删除可以算为左为空/右为空的情况，所以只需考虑左为空/右为空 或者 删除节点有左孩子和右孩子节点 即可
左为空
左为空时，使用parent节点去接收cur的右子树，但是还需判断下cur的右子树节点在parent的左子树还是右子树
需要考虑cur节点作为根的情况，此时的parent节点为NULL，NULL->right就会报错
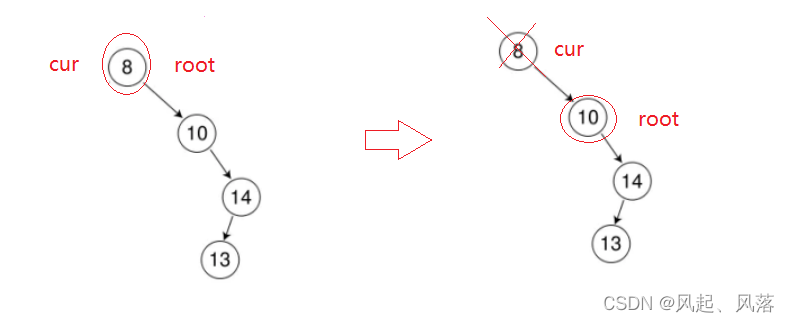
为了解决这个问题，把cur的右子树的节点作为根，然后直接删除cur节点
右为空
右为空时，使用parent节点去接收cur的左子树，但是还需判断下cur的左子树节点在parent的左子树还是右子树
当cur作为根节点时，此时parent为NULL,就会报错
所以要把cur作为根节点的情况单独处理
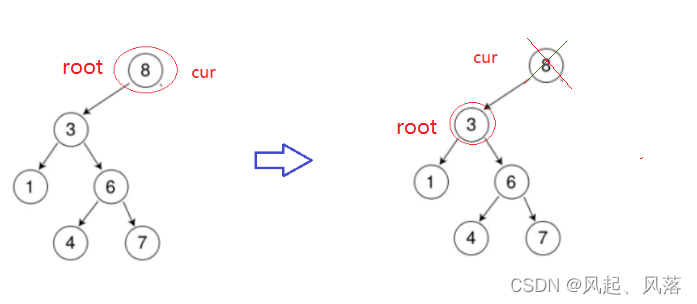
把cur的左子树的节点作为根，然后直接删除cur节点
删除节点有左孩子和右孩子节点
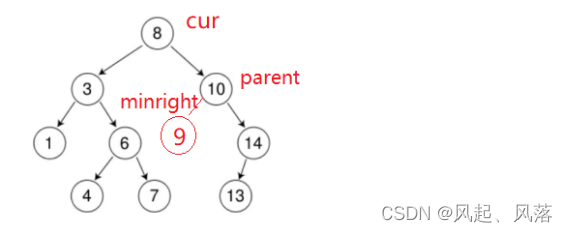
当找到minright时，minright在9节点位置上，minright可以替代cur的位置，替cur照顾两个孩子，但是minright本身也是有可能有孩子的，所以还需要找到minright的上一个父节点parent，同时需要判断下minright节点是parent节点的左孩子还是有孩子
pminright初始化不能为NULL，若为空，若不进入while循环，则无法更新pminright值，
导致NULL->left，从而报错
，minright不一定是minright的左子树，也有可能是pminright的右子树 ，所以需要判断下
整体代码
//删除
bool Erase(const K& key)
{
//将第一种和第二种看作一种
Node* parent = nullptr;//记录cur之前的节点
Node* cur = _root;
while (cur!=NULL)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
//相等则说明数据存在，要删除
//1.左为空
if (cur->_left == nullptr)
{
if (cur == _root)//当cur作为根节点时
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)//若cur在parent节点的左边
{
parent->_left = cur->_right;
}
else//若cur在parent节点的右边
{
parent->_right = cur->_right;
}
}
delete cur;
}
//2.右为空
else if (cur->_right == nullptr)
{
if (cur == _root)//当cur作为根节点时
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)//若cur在parent节点的左边
{
parent->_left = cur->_left;
}
else//若cur在parent节点的右边
{
parent->_right = cur->_left;
}
}
delete cur;
}
//3.请保姆
else
{
//寻找右子树的最小节点
Node* pminright = cur;
Node* minright = cur->_right;//右子树的最小节点
//最左节点
while (minright->_left)//找到最小节点
{
pminright = minright;//记录minright之前的节点
minright = minright->_left;
}
cur->_key = minright->_key;
//由于不知道minright是pminright的左子树还是右子树 ，所以需要判断下
//再将minright的右子树pminright
if (pminright->_left == minright)
{
pminright->_left = minright->_right;
}
else
{
pminright->_right = minright->_right;
}
delete minright;
}
return true;
}
}
//说明要删除的数据不存在
return false;
}
二叉搜索树的实现 (递归)
递归实现，全都使用了函数嵌套的方式，与非递归的中序遍历的方式相同，是为了使用_root这个定义在类中的成员变量
查找
bool _FindR(Node * root, const K & key)
{
if (root == nullptr)
{
return false;
}
if (root->_key == key)
{
return true;
}
if (root->_key < key)
{
retrun _FindR(root->_right, key);
}
else
{
retrun _FindR(root->_left, key);
}
}
bool FindR(const K & key)
{
return _FindR(_root, key);
}
插入
bool _InsertR(Node*&root,const K&key)//插入
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if(root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
bool InsertR(const K& key)
{
return _InsertR(_root,key);
}
通过引用的方式解决遇见NULL连接新节点的问题
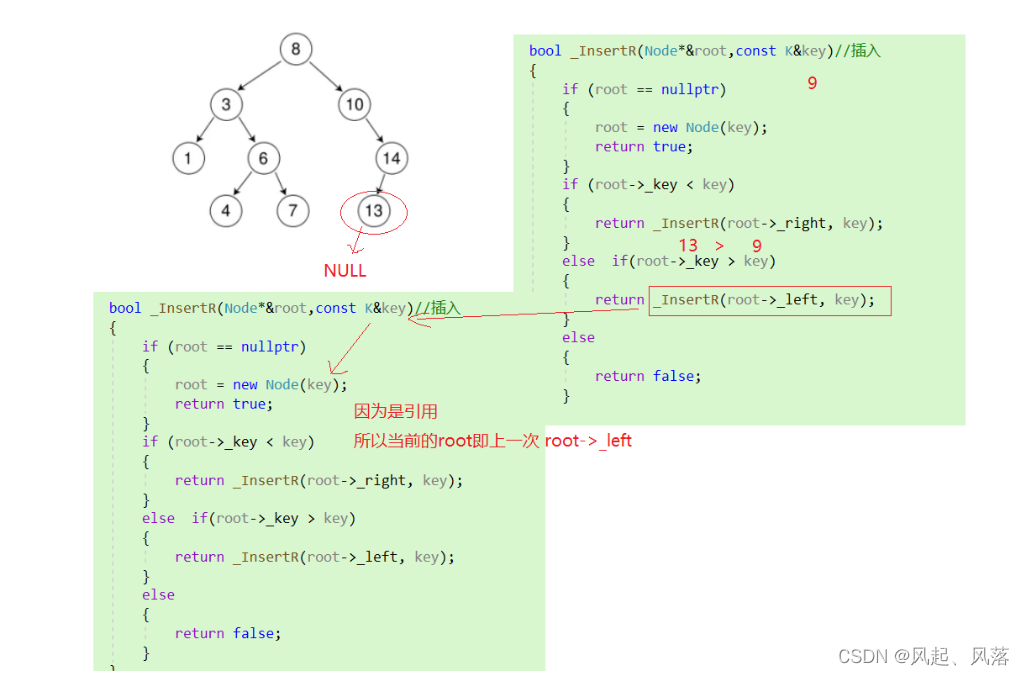
因为引用的原因，所以root==NULL进入if判断时， root作为上一个节点左指针的别名，相当于 root->_left 新创建了一个节点，直接与二叉树连接起来了
就不用像非递归一样考虑创建节点后，与它的上一个节点连接的问题
删除
删除节点有左孩子和右孩子节点
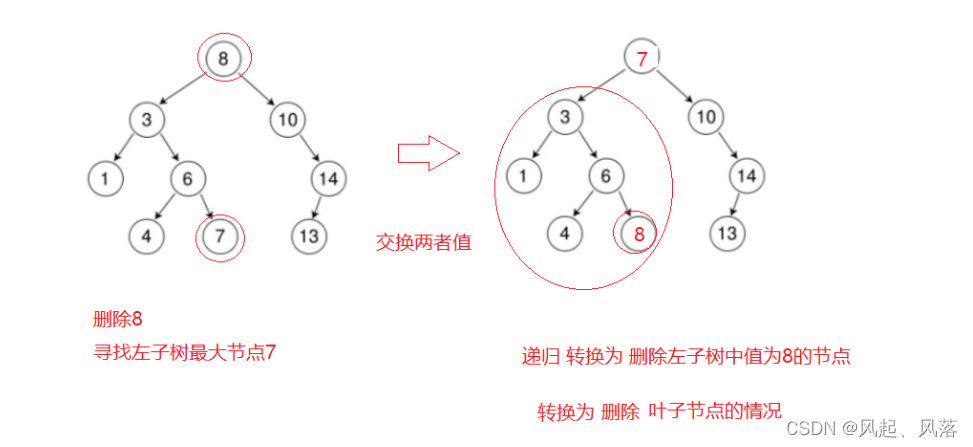
bool _EraseR(Node*&root,const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return EraseR(root->_right, key);
}
else if (root->_key > key)
{
return EraseR(root->_left, key);
}
else
{
//开始删除
Node* del= root;//保存要删除的节点
if (root->_left == nullptr)//左为空
{
root = root->_right;
}
else if (root->_right == nullptr)//右为空
{
root = root->_left;
}
else
{
//替代法
Node* maxleft = root->_left;
//在左子树中寻找最右 作为左子树最大节点
while (maxleft->_right != NULL)
{
maxleft = maxleft->_right;
}
swap(maxleft, root);
return EeaseR(root->_left, key);
}
delete del;
return true;
}
}
bool EraseR(const K&key)
{
return _EraseR(_root,key);
}
二叉搜索树实现的整体代码
#pragma once
#include<iostream>
using namespace std;
template <class K>
//BSTree -- BinarySearchTree
struct BSTreeNode
{
BSTreeNode<K>* _left;//左
BSTreeNode<K>* _right;//右
K _key;//关键字
BSTreeNode(const K& key)
:_left(nullptr), _right(nullptr), _key(key)
{
}
};
template <class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
~BSTree()//析构
{
Destroy(_root);
_root = nullptr;
}
/*BSTree(const BSTree<K>& t)
{
}
void cpoy(Node*root)
{
}*/
//插入
bool Insert(const K& key)
{
if (_root == NULL)//若root根节点为nullptr
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;//用于接收cur之前的节点
while (cur != NULL)
{
if (cur->_key > key)//若插入的值比cur值小
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)//若插入的值比cur值大
{
parent = cur;
cur = cur->_right;
}
else//若相等，则直接返回false
{
return false;
}
}
//遇见空指针，连接新节点
//由于不知道parent的左还是右连接key，所以需要判断
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
//中序遍历
void inorder()
{
_inorder(_root);
}
void _inorder(Node*root)
{
if (root == NULL)
{
return;
}
_inorder(root->_left);//左
cout << root->_key << " ";//根
_inorder(root->_right);//右
}
//查找
bool Find(const K& key)
{
Node* cur = _root;
while (cur != NULL)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return true;
}
}
return false;
}
//删除
bool Erase(const K& key)
{
//将第一种和第二种看作一种
Node* parent = nullptr;//记录cur之前的节点
Node* cur = _root;
while (cur!=NULL)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
//相等则说明数据存在，要删除
//1.左为空
if (cur->_left == nullptr)
{
if (cur == _root)//当cur作为根节点时
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)//若cur在parent节点的左边
{
parent->_left = cur->_right;
}
else//若cur在parent节点的右边
{
parent->_right = cur->_right;
}
}
delete cur;
}
//2.右为空
else if (cur->_right == nullptr)
{
if (cur == _root)//当cur作为根节点时
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)//若cur在parent节点的左边
{
parent->_left = cur->_left;
}
else//若cur在parent节点的右边
{
parent->_right = cur->_left;
}
}
delete cur;
}
//3.请保姆
else
{
//寻找右子树的最小节点
Node* pminright = cur;
Node* minright = cur->_right;//右子树的最小节点
//最左节点
while (minright->_left)//找到最小节点
{
pminright = minright;//记录minright之前的节点
minright = minright->_left;
}
cur->_key = minright->_key;
//由于不知道minright是pminright的左子树还是右子树 ，所以需要判断下
//再将minright的右子树pminright
if (pminright->_left == minright)
{
pminright->_left = minright->_right;
}
else
{
pminright->_right = minright->_right;
}
delete minright;
}
return true;
}
}
//说明要删除的数据不存在
return false;
}
//--------- 递归
bool _FindR(Node * root, const K & key)//查找
{
if (root == nullptr)
{
return false;
}
if (root->_key == key)
{
return true;
}
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else
{
return _FindR(root->_left, key);
}
}
bool FindR(const K & key)
{
return _FindR(_root, key);
}
bool _InsertR(Node*&root,const K&key)//插入
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if(root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
bool InsertR(const K& key)
{
return _InsertR(_root,key);
}
bool _EraseR(Node*&root,const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return EraseR(root->_right, key);
}
else if (root->_key > key)
{
return EraseR(root->_left, key);
}
else
{
//开始删除
Node* del= root;//保存要删除的节点
if (root->_left == nullptr)//左为空
{
root = root->_right;
}
else if (root->_right == nullptr)//右为空
{
root = root->_left;
}
else
{
//替代法
Node* maxleft = root->_left;
//在左子树中寻找最右 作为左子树最大节点
while (maxleft->_right != NULL)
{
maxleft = maxleft->_right;
}
swap(maxleft, root);
return EeaseR(root->_left, key);
}
delete del;
return true;
}
}
bool EraseR(const K&key)
{
return _EraseR(_root,key);
}
void Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
private:
Node* _root = nullptr;
};
风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。
站长推荐
- U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》