0 专栏介绍

?附C++/Python/Matlab全套代码?课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

?详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

1 RRT-Connect基本原理

在原始RRT算法中，终点附近的区域信息并不能得到有效利用，为了解决这个问题，可以分别以起点和终点为根节点进行双搜索树双向扩展，当两棵树建立连接时可回溯可行路径，称为RRT-Connect算法

2 RRT-Connect vs. RRT

对原始版本RRT算法不了解的同学请看：路径规划 | 图解快速随机扩展树RRT算法(附ROS C++/Python/Matlab仿真)。与RRT算法相比，RRT-Connect有什么特别的优势呢？

• 更高效的路径搜索：RRT-Connect算法通过引入Connect启发式算法，将传统的扩张函数替换为一种贪婪策略——允许在更长的距离上移动，而不仅限于单步扩展，从而在探索可行路径时具有更高的效率。这使得RRT-Connect能够更快地收敛到可行路径，尤其是在没有微分约束的情况下。
• 更好的全局规划性能：RRT-Connect算法的另一个优点是它能够同时从起始配置和目标配置开始扩展RRT。这种双向扩展可以更好地探索搜索空间，并在找到可行路径时更快地连接起始配置和目标配置。这使得RRT-Connect算法在全局路径规划方面更为有效，并且具有更好的搜索性能。

RRT-Connect算法流程如下所示

3 ROS C++算法实现

核心代码如下所示

bool RRTConnect::plan(const unsigned char* gloal_costmap, const Node& start, const Node& goal, std::vector<Node>& path,
                      std::vector<Node>& expand)
{
  sample_list_f_.clear();
  sample_list_b_.clear();
  // copy
  start_ = start, goal_ = goal;
  costs_ = gloal_costmap;
  sample_list_f_.insert(start);
  sample_list_b_.insert(goal);
  expand.push_back(start);
  expand.push_back(goal);

  // main loop
  int iteration = 0;
  while (iteration < sample_num_)
  {
    // generate a random node in the map
    Node sample_node = _generateRandomNode();

    // obstacle
    if (gloal_costmap[sample_node.id_] >= lethal_cost_ * factor_)
      continue;

    // visited
    if (sample_list_.find(sample_node) != sample_list_.end())
      continue;

    // regular the sample node
    Node new_node = _findNearestPoint(sample_list_f_, sample_node);
    if (new_node.id_ == -1)
      continue;
    else
    {
      sample_list_f_.insert(new_node);
      expand.push_back(new_node);
      // backward exploring
      Node new_node_b = _findNearestPoint(sample_list_b_, new_node);
      if (new_node_b.id_ != -1)
      {
        sample_list_b_.insert(new_node_b);
        expand.push_back(new_node_b);
        // greedy extending
        while (true)
        {
          double dist = std::min(max_dist_, _dist(new_node, new_node_b));
          double theta = _angle(new_node_b, new_node);
          Node new_node_b2;
          new_node_b2.x_ = new_node_b.x_ + (int)(dist * cos(theta));
          new_node_b2.y_ = new_node_b.y_ + (int)(dist * sin(theta));
          new_node_b2.id_ = grid2Index(new_node_b2.x_, new_node_b2.y_);
          new_node_b2.pid_ = new_node_b.id_;
          new_node_b2.g_ = dist + new_node_b.g_;

          if (!_isAnyObstacleInPath(new_node_b, new_node_b2))
          {
            sample_list_b_.insert(new_node_b2);
            expand.push_back(new_node_b2);
            new_node_b = new_node_b2;
          }
          else
            break;

          // connected -> goal found
          if (new_node_b == new_node)
          {
            path = _convertClosedListToPath(new_node_b);
            return true;
          }
        }
      }
    }

    // swap
    if (sample_list_b_.size() < sample_list_f_.size())
      std::swap(sample_list_f_, sample_list_b_);

    iteration++;
  }
  return false;
}

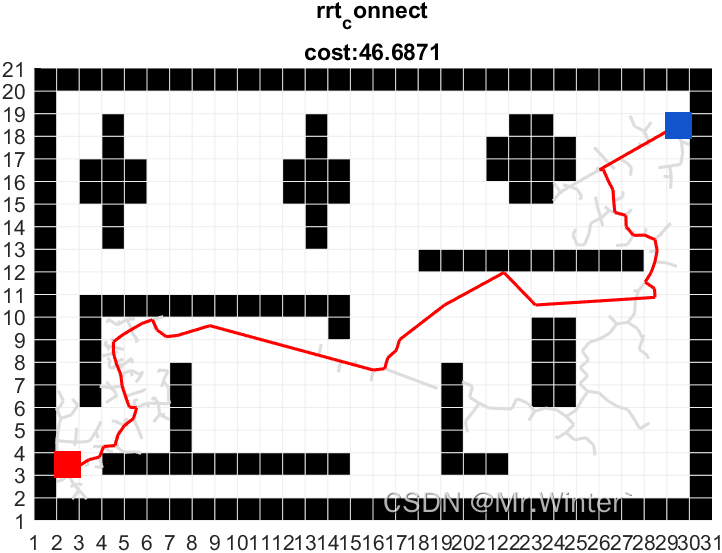
运行效果图

4 Python算法实现

核心代码如下所示

def plan(self):
	for _ in range(self.sample_num):
	    # generate a random node in the map
	    node_rand = self.generateRandomNode()            
	    # generate new node
	    node_new = self.getNearest(self.sample_list_f, node_rand)
	    if node_new:
	        self.sample_list_f.append(node_new)
	        # backward exploring
	        node_new_b = self.getNearest(self.sample_list_b, node_new)
	        if node_new_b:
	            self.sample_list_b.append(node_new_b)
	            # greedy extending
	            while True:
	                dist = min(self.max_dist, self.dist(node_new, node_new_b))
	                theta = self.angle(node_new_b, node_new)
	                node_new_b2 = Node((node_new_b.current[0] + dist * math.cos(theta),
	                                   (node_new_b.current[1] + dist * math.sin(theta))),
	                                    node_new_b.current, node_new_b.g + dist, 0)
	                if not self.isCollision(node_new_b2, node_new_b):
	                    self.sample_list_b.append(node_new_b2)
	                    node_new_b = node_new_b2
	                else:
	                    break
	
	                if node_new_b == node_new:
	                    return self.extractPath(node_new)
	
	    if len(self.sample_list_b) < len(self.sample_list_f):
	        self.sample_list_f, self.sample_list_b = self.sample_list_b, self.sample_list_f
	
	return 0, None

5 Matlab算法实现

核心代码如下所示

% main loop
for i=1: param.sample_num
    % generate a random node in the map
    node_rand = generate_node(goal, param);

    % generate new node
    [node_new, success] = get_nearest(sample_list_f, node_rand, map, param);
    if success
        sample_list_f = [node_new; sample_list_f];
        % backward exploring
        [node_new_b, success_b]  = get_nearest(sample_list_b, node_new(1:2), map, param);
        if success_b
             sample_list_b = [node_new_b; sample_list_b];
             % greedy extending
             while true
                 distance = min(param.max_dist, dist(node_new(1:2), node_new_b(1:2)'));
                 theta = angle(node_new_b, node_new);
                 node_new_b2 = [node_new_b(1) + distance * cos(theta), ...
                                              node_new_b(2) + distance * sin(theta), ...
                                              node_new_b(3) + distance, ...
                                              node_new_b(1:2)];
                if ~is_collision(node_new_b2(1:2), node_new_b(1:2), map, param)
                    sample_list_b = [node_new_b2; sample_list_b];
                    node_new_b = node_new_b2;
                else
                    break
                end
                % goal found
                if node_new_b(1) == node_new(1) && node_new_b(2) == node_new(2)
                    flag = true;
                    cost = sample_list_f(1, 3) + sample_list_b(1, 3);
                    path = extract_path(sample_list_f, sample_list_b, start, goal);
                    expand = [sample_list_f; sample_list_b];
                    return
                end
             end
        end
    end
    
    [len_f, ~] = size(sample_list_f); [len_b, ~] = size(sample_list_b);
    if len_b < len_f
        temp = sample_list_f;
        sample_list_f = sample_list_b;
        sample_list_b = temp;
    end
end

完整工程代码请联系下方博主名片获取

? 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …