赛题介绍

背景

2021 CCF BDCI 基于飞桨实现花样滑冰选手骨骼点动作识别赛题再开放，旨在探索基于骨骼点的细粒度人体动作识别方法，要求参赛选手构建基于骨骼点的时空细粒度动作识别模型，完成测试集的动作识别任务。

人体运动分析是近几年众多领域研究的热点问题。在学科交叉研究方面，人体运动分析涉及到计算机科学、运动人体科学、环境行为学和材料科学等。随着相关研究的逐步深入以及计算机视觉、5G通信的飞速发展，人体运动分析技术已应用于自动驾驶、影视创作、安防异常事件监测和体育竞技分析、康复等实际场景，人体运动分析已成为人工智能领域研究的前沿课题，此类研究也将在竞技体育、运动康复、日常健身等方面发挥非常重大的意义。

然而，目前的研究数据普遍缺少细粒度语义信息，导致现存的分割或识别任务缺少时空细粒度动作语义模型。相较于图片细粒度研究，时空细粒度语义的人体动作具有动作类内方差大、类间方差小等特点，这将导致由细粒度语义产生的一系列问题，而利用粗粒度语义的识别模型进行学习也难以获得理想的结果。

数据集

在本次比赛最新发布的数据集中，所有视频素材均从2017-2020 年的花样滑冰锦标赛中采集得到。源视频素材中视频的帧率被统一标准化至每秒30 帧，图像大小被统一标准化至1080 * 720 ，以保证数据集的相对一致性。之后通过2D姿态估计算法Open Pose，对视频进行逐帧骨骼点提取，最后以.npy格式保存数据集。请各位选手基于本次比赛最新发布的训练集数据训练模型，并基于本次比赛最新发布的测试集数据提交对应结果文件。

|–train.zip
|–train_data.npy
|–train_label.npy
|–test_A.zip
|–test_A_data.npy
|–test_B.zip
|–test_B_data.npy

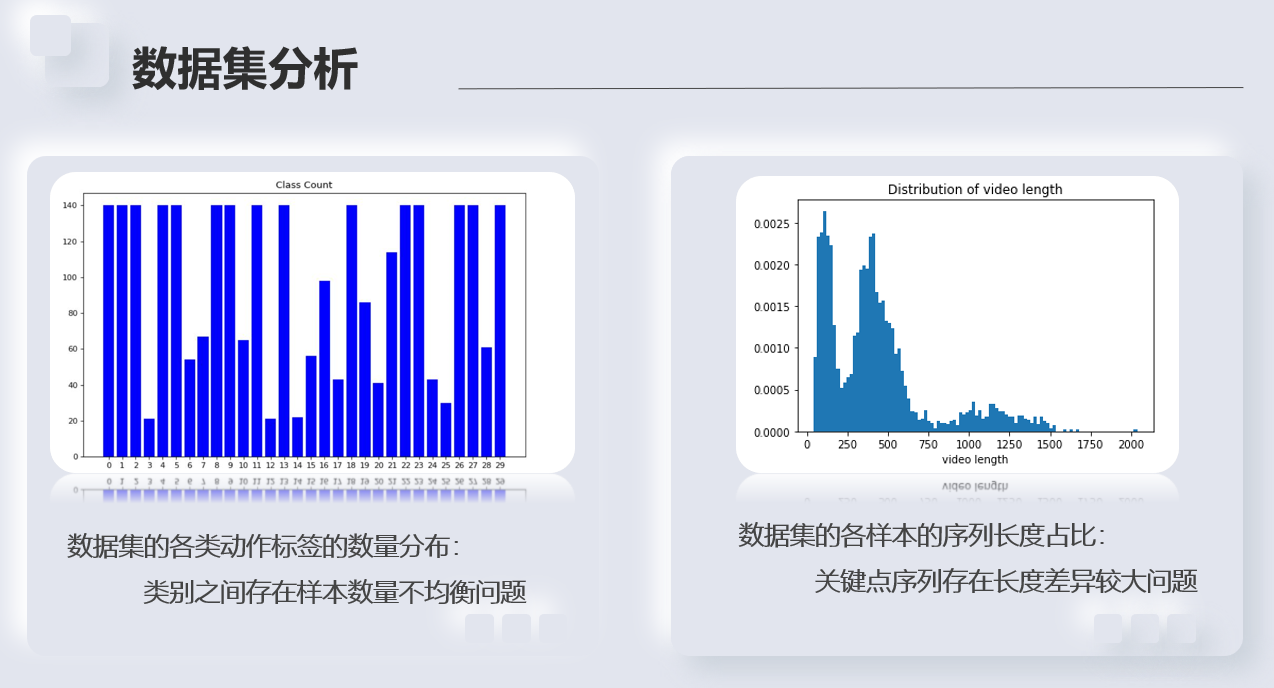
• 本次比赛最新发布的数据集共包含30个类别，训练集共2922个样本，A榜测试集共628个样本，B榜测试集共634个样本；
• train_label.npy文件通过np.load()读取后，会得到一个一维张量，张量中每一个元素为一个值在0-29之间的整形变量，代表动作的标签；
• data.npy文件通过np.load()读取后，会得到一个形状为N×C×T×V×M的五维张量，每个维度的具体含义如下：

• 骨架示例图：

思路讲解

这些过程都在该项目的各个版本中。
Steps：

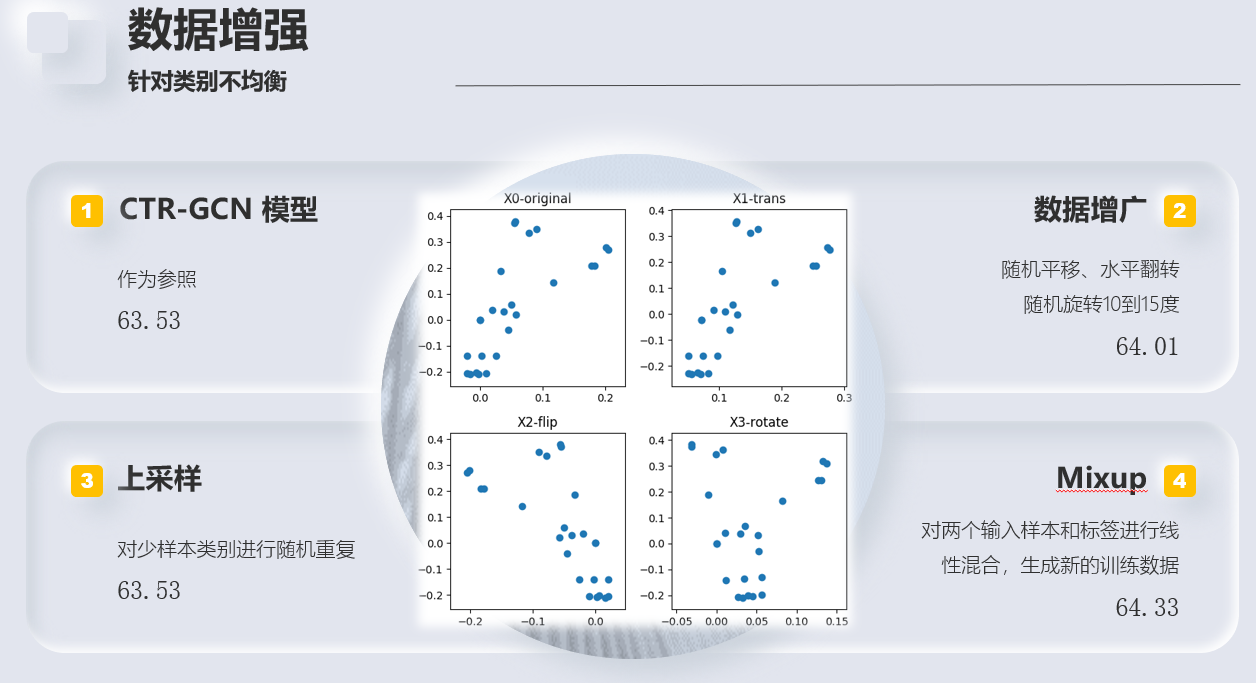
1. 模型选择 -> CTR-GCN
2. 优化（针对数据集的类别不平衡和序列长度不均问题）
3. 高阶特征提取，多流框架
   
   
   

backbone 模型

介绍了三种模型，ST-GCN 是比赛提供的 Baseline 模型，在此基础上，实现了 2s-AGCN 和 CTR-GCN 模型。见下文模型介绍。

三种模型均基于大赛提供的 PaddleVideo 框架。

文件结构 – PaddleVideo 框架

博文参考：PaddleVideo 简介以及文件目录详解

PaddleVideo 是一个基于飞桨的视频理解工具库，它支持视频数据标注工具、轻量化的RGB和骨骼点的行为识别模型、以及视频标签和运动检测等实用应用。

configs 文件夹

configs 文件夹存放各种模型和数据集的 配置文件。PaddleVideo 支持 通过修改配置文件 来 实现不同的模型和数据集的组合，以及进行 模型训练、测试、推理等操作。

PaddleVideo 分类别 存放不同模型和数据集的配置文件：
PaddleVideo/configs/ 下有 recognition（行为识别）、segmentation（视频分割）、localization（动作定位）、detection（动作检测） 等文件夹。

举例来说， recognition 文件夹下有很多行为识别方向的模型和数据集的 配置文件，如图：

paddlevideo 文件夹

paddlevideo 文件夹存放 视频模型库相关的代码和文件 的文件夹。

• paddlevideo/utils 文件夹中包含了一些 通用的工具函数 和 预处理方法，用于 辅助视频数据的加载、预处理和后处理 等。
• paddlevideo/tasks 文件夹的作用是存放一些 用于定义和执行不同的机器学习任务的类或函数。
• paddlevideo/loader 文件夹的作用是存放一些用于 加载和处理数据 的类或函数。
• paddlevideo/modeling 文件夹的作用是存放一些用于 构建和定义模型 的类或函数。
• paddlevideo/solver 文件夹的作用是存放一些用于 优化和求解模型 的类或函数。
• paddlevideo/metrics 文件夹存放一些用于 评估模型性能的指标 的类或函数。

模型介绍

1. ST-GCN – Baseline 模型

整体结构

ST-GCN是AAAI 2018中提出的经典的基于骨骼的行为识别模型，不仅为解决基于人体骨架关键点的人类动作识别问题提供了新颖的思路，在标准的动作识别数据集上也取得了较大的性能提升。算法整体框架如下图所示：

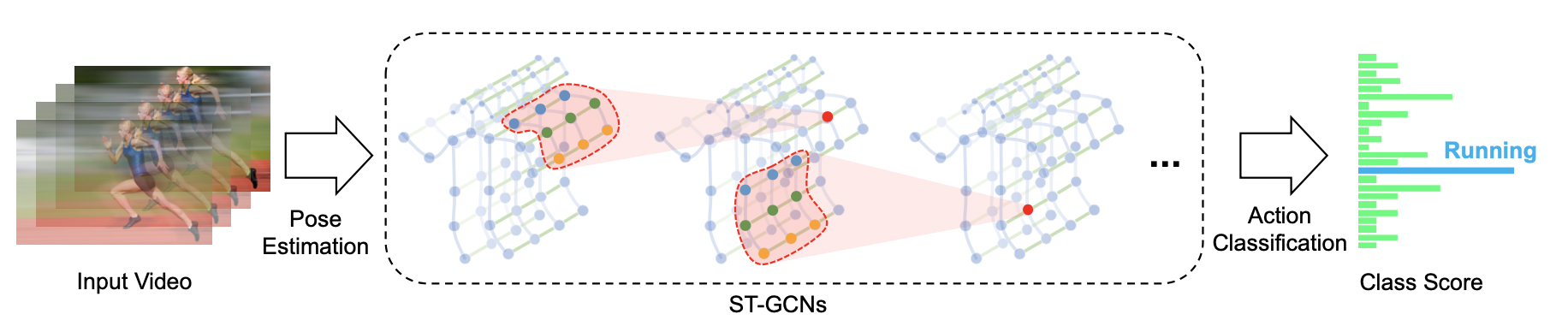
时空图卷积网络模型 ST-GCN 通过将图卷积网络（GCN）和时间卷积网络（TCN）结合起来，扩展到时空图模型，设计出了用于行为识别的骨骼点序列通用表示，该模型将人体骨骼表示为图，其中图的每个节点对应于人体的一个关节点。图中存在两种类型的边，即符合关节的自然连接的空间边（spatial edge）和在连续的时间步骤中连接相同关节的时间边（temporal edge）。在此基础上构建多层的时空图卷积，它允许信息沿着空间和时间两个维度进行整合。

ST-GCN 的网络结构大致可以分为三个部分，首先，对网络输入一个五维矩阵$\left(N,C,T,V;M\right)$.其中N为视频数据量；C为关节特征向量，包括$\left(x,y,acc\right)$；T为视频中抽取的关键帧的数量；V表示关节的数量，在本项目中采用25个关节数量；M则是一个视频中的人数，然后再对输入数据进行Batch Normalization批量归一化，接着，通过设计ST-GCN单元，引入ATT注意力模型并交替使用GCN图卷积网络和TCN时间卷积网络，对时间和空间维度进行变换，在这一过程中对关节的特征维度进行升维，对关键帧维度进行降维，最后，通过调用平均池化层、全连接层，并后接 SoftMax 层输出，对特征进行分类。

GCN部分

图卷积网络（Graph Convolutional Network，GCN）借助图谱的理论来实现空间拓扑图上的卷积，提取出图的空间特征，具体来说，就是将人体骨骼点及其连接看作图，再使用图的邻接矩阵、度矩阵和拉普拉斯矩阵的特征值和特征向量来研究该图的性质。
在原论文中，作者提到他们使用了「Kipf, T. N., and Welling, M. 2017. Semi-supervised classification with graph convolutional networks. In ICLR 2017」中的GCN架构，其图卷积数学公式如下:
$$f_{out}={\Lambda }^{-\frac{1}{2}}\left(A+I\right){\Lambda }^{-\frac{1}{2}}{f}_{in}W$$

其中，$f_{out}$为输出，A为邻接矩阵，I为单位矩阵，$A^{ii}={\sum }_j(A^{ij}+I^{ij})$, W是需要学习的空间矩阵。
原文中，作者根据不同的动作划分为了三个子图$\left(A_1,A_2,A_3\right)$，分别表达向心运动、离心运动和静止的动作特征。

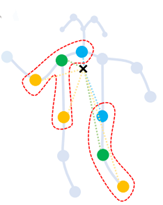
在实际的应用中，最简单的图卷积已经能达到很好的效果，所以实现中采用的是$D^{-1}A$图卷积核。D为度矩阵。

TCN部分

ST-GCN单元通过GCN学习空间中相邻关节的局部特征，而时序卷积网络（Temporal convolutional network，TCN）则用于学习时间中关节变化的局部特征。卷积核先完成一个节点在其所有帧上的卷积，再移动到下一个节点，如此便得到了骨骼点图在叠加下的时序特征。对于TCN网络，项目中通过使用$9\times 1$的卷积核进行实现。为了保持总体的特征量不变，当关节点特征向量维度©成倍变化时，步长取2，其余情况步长取1。

2. 2s-AGCN

参见博文：
2s-AGCN 论文解读
2s-AGCN 代码理解

2s-AGCN 是发表在CVPR2019上的一篇针对 ST-GCN 进行改进的文章，文章提出双流自适应卷积网络，针对原始 ST-GCN 的缺点进行了改进。在现有的基于 GCN 的方法中，图的拓扑是手动设置的，并且固定在所有图层和输入样本上。另外，骨骼数据的二阶信息（骨骼的长度和方向）对于动作识别自然是更有益和更具区分性的，在当时方法中很少进行研究。因此，文章主要提出一个基于骨架节点和骨骼两种信息融合的双流网络，并在图卷积中的邻接矩阵加入自适应矩阵，大幅提升骨骼动作识别的准确率，也为后续的工作奠定了基础（后续的骨骼动作识别基本都是基于多流的网络框架）。

从名字可以看出，文章主要创新点有两个，一个是自适应性，另外一个是双流网络。

自适应图卷积

这是针对 ST-GCN 的第一个缺点进行的改进，对邻接矩阵进行了改进。

图的拓扑实际上是由邻接矩阵和掩码决定的，分别为 $A_k$ 和 $M_k$。$A_k$ 决定了两个顶点之间是否有连接，$M_k$ 决定了连接的强度。为了使图结构自适应，将公式改为如下形式：$${\mathbf{f}}_{out}=\sum _k^{K_v}{\mathbf{W}}_k{\mathbf{f}}_{in}({\mathbf{A}}_k+{\mathbf{B}}_k+{\mathbf{C}}_k)\text{\hspace{1em}(3)}$$主要区别在于图的邻接矩阵，它分为三部分：$A_k$，$B_k$ 和 $C_k$。

第一部分 $(A_k)$ 与 ST-GCN 原公式中原归一化 $N\times N$ 邻接矩阵 $A_k$ 相同，它代表人体的物理结构。

第二部分 $(B_k)$ 也是一个 $N\times N$ 邻接矩阵。与 $A_k$ 相比，$B_k$ 的元素在训练过程中与其他参数一起参数化和优化。$B_k$ 的值没有约束，这意味着图完全是根据训练数据学习的。注意，矩阵中的元素可以是任意值。它不仅表明两个关节之间是否存在连接，而且还表明连接的强度。

第三部分 $(C_k)$ 是一个依赖于数据的图，它为每个样本学习一个唯一的图。

自适应图卷积层的总体结构如下图所示：

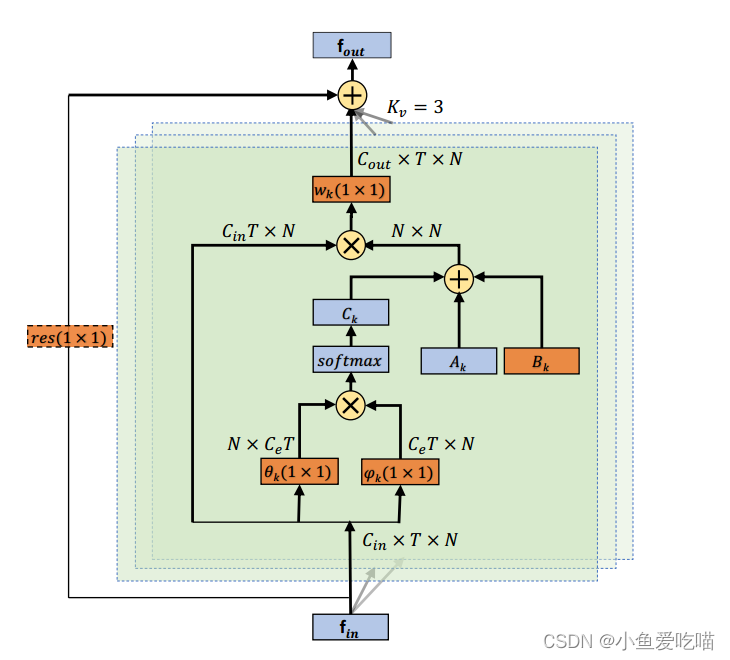
每一层共有三种类型的图，分别是 $A_k$，$B_k$ 和 $C_k$。橙色框表示该参数是可学习的。$(1\times 1)$ 为卷积核的大小，$K_v$ 表示子集的数量。$\oplus$ 表示按元素求和，$\otimes$ 表示矩阵乘法。残差框(虚线)仅在 $C_{in}$ 与 $C_{out}$ 不相同时才需要。

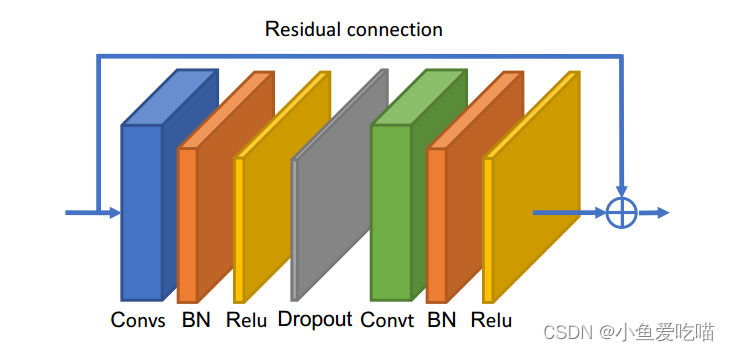
上图为自适应图卷积块的说明，Convs 表示空间 GCN，Convt 表示时间 GCN，后面都有 BN 层和 ReLU 层。此外，为每个块添加一个残差连接。

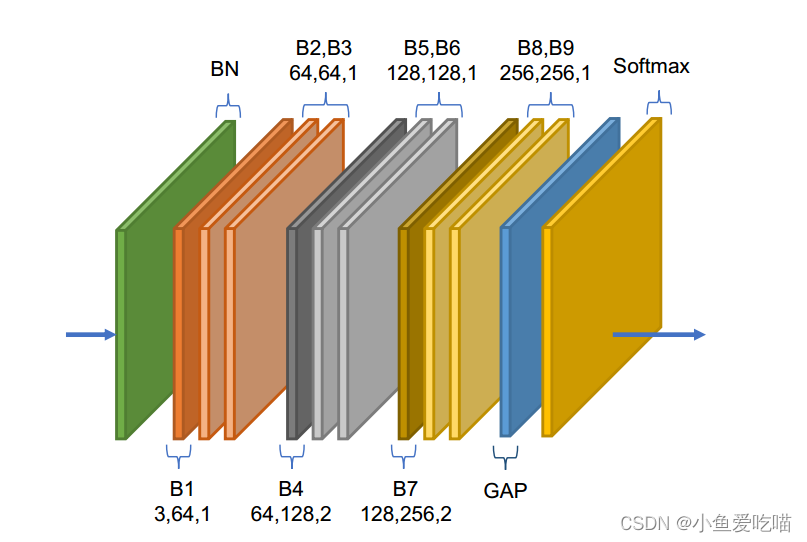
上图为自适应图卷积层的说明，是基本块的堆栈。图中，每个块的三个数字分别表示输入通道数、输出通道数和步幅。GAP 表示全局平均池化层。

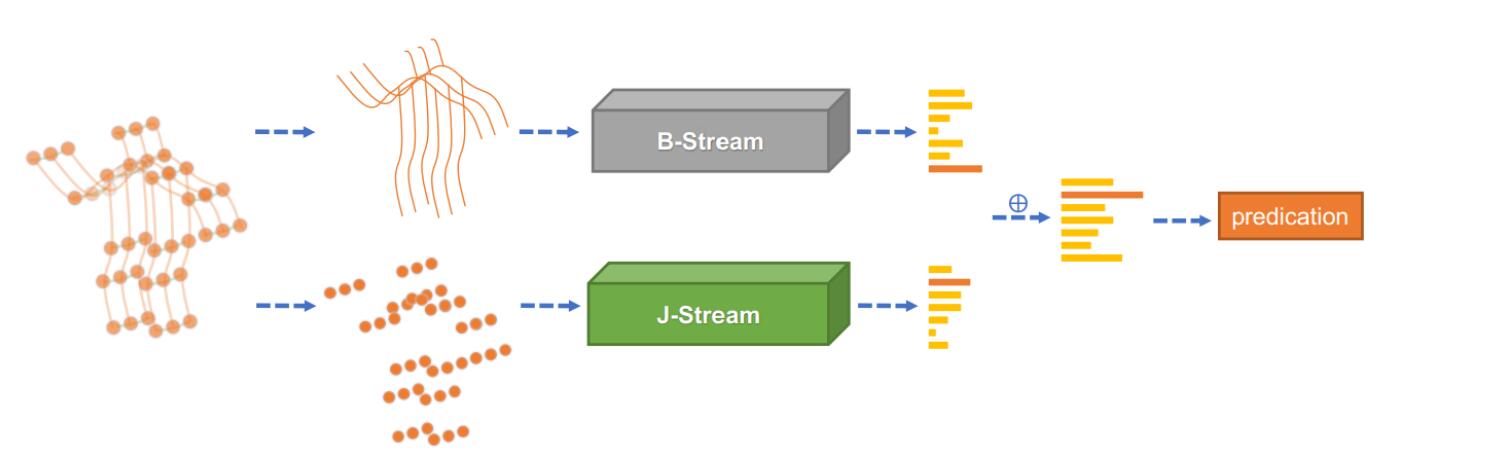
双流网络

我们使用 J-stream 和 B-stream 分别表示关节和骨骼的网络。整体架构(2s-AGCN)如下图所示。

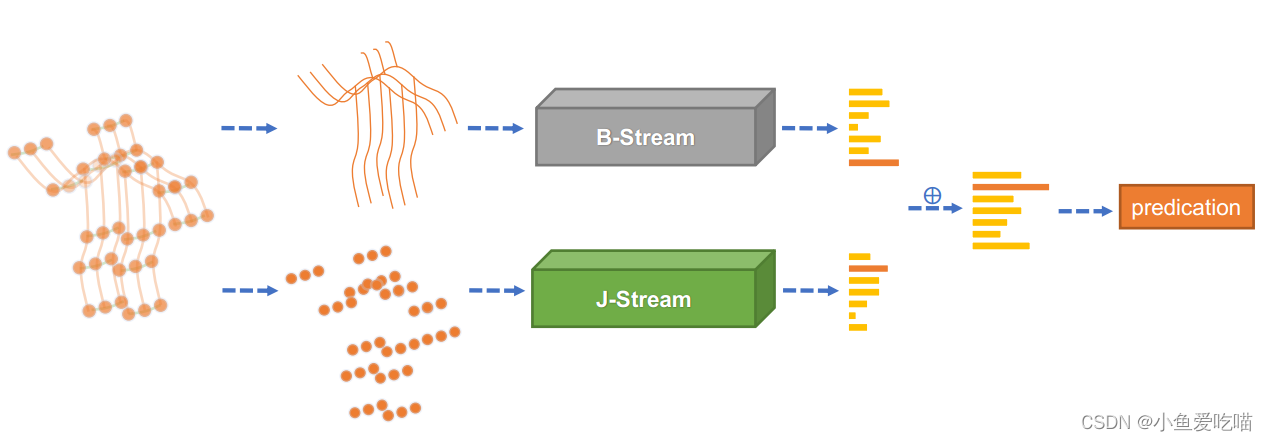
给定一个样本，我们首先根据关节数据计算骨骼数据。然后将关节数据和骨骼数据分别输入 J-stream 和 B-stream。最后，将两个流的 $softmax$ 分数相加，得到融合分数并预测动作标签。

3. CTR-GCN

参见博文：
CTR-GCN 论文解读
CTR-GCN 代码理解

CTR-GCN 是 ICCV 2021提出的基于骨骼的行为识别模型，通过将改动应用在具有拓扑结构的人体骨骼数据上的图卷积，使用时空图卷积提取时空特征进行行为识别，提升了基于骨骼的行为识别任务精度。

提出了一种新的通道拓扑优化图卷积(CTR-GC)，以动态学习不同的拓扑，并有效地聚合不同通道中的关节特征，用于基于骨骼的动作识别。提出的 CTR-GC 通过学习共享拓扑作为所有通道的通用先验，并使用每个通道的特定通道相关性对其进行细化，从而对通道拓扑进行建模。

这篇文章最大的创新就是细化训练了拓扑结构，CTR-GCN 的代码完全基于2s-AGCN 改进的。

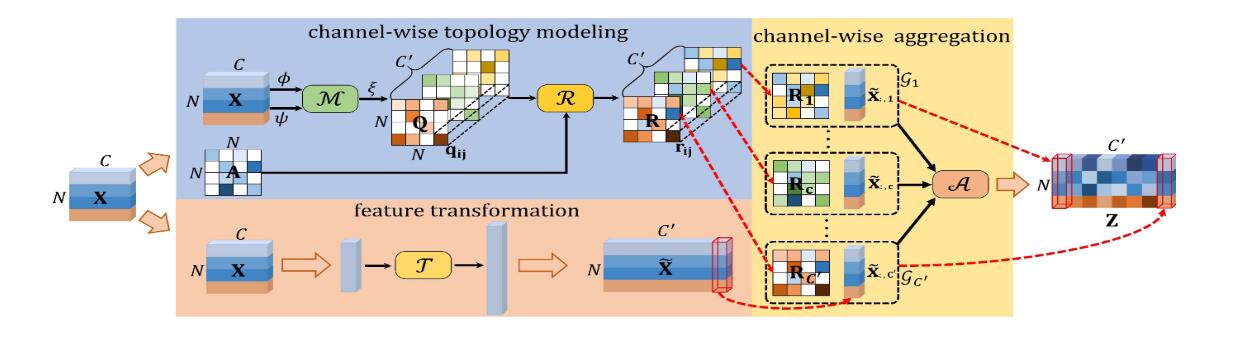
上图为所提出的通道拓扑优化图卷积的框架。基于通道的拓扑建模使用推断出的特定于通道的相关性来细化可训练的共享拓扑。特征转换的目的是将输入特征转换为高级表示形式。最终，通过通道聚合获得输出特征。

CTR-GC

CTR-GC 包含三个部分：

• 特征转换，通过变换函数 $\mathcal{T}(\cdot )$ 进行特征变换；
• 通道拓扑建模，包括相关建模函数 $\mathcal{M}(\cdot )$ 和细化函数 $\mathcal{R}(\cdot )$；
• 通道聚合，由聚合函数 $\mathcal{A}(\cdot )$ 完成。

给定输入特征 $\mathbf{X}\in {\mathbb{R}}^{N\times C}$，则 CTR-GC 的输出 $\mathbf{Z}\in {\mathbb{R}}^{N\times C^{\prime }}$ 表示为$$\mathbf{Z}=\mathcal{A}(\mathcal{T}(\mathbf{X}),\mathcal{R}(\mathcal{M}(\mathbf{X}),\mathbf{A}))\text{\hspace{1em}(2)}$$其中 $\mathbf{A}\in {\mathbb{R}}^{N\times N}$ 为可学习共享拓扑。