1、时间复杂度

• 算法在编写成可执行程序后，运行时需要耗费时间资源和空间(内存)资源，因此衡量一个算法的好坏一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度
• 时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间。

（1）时间复杂度只保留最高阶项

（2）同级别的未知数不能省略

（3）常数次的时间复杂度为O(1)

（4）常数×未知数，常数可以省略

（5）关注算法的最坏运行情况

（6）冒泡排序O(N^2)

（7）二分查找O(log2(N))

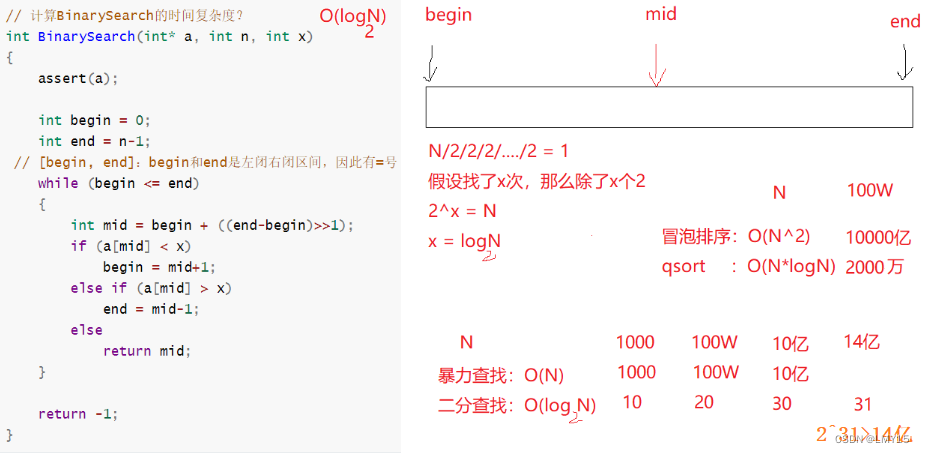
（8）递归调用对比

（9）斐波那契递归O(2^N)

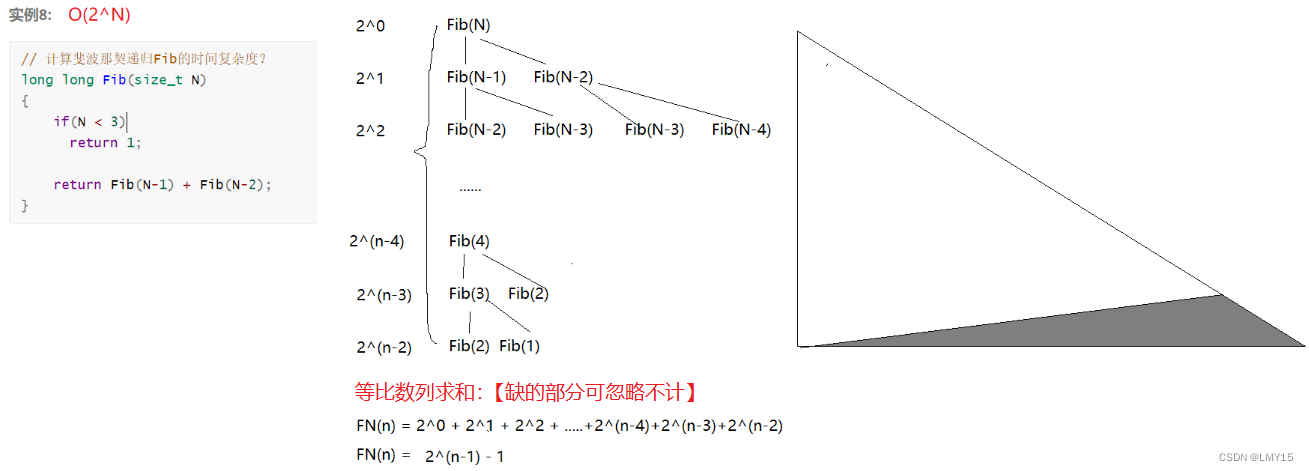
（10）Leetcode题目链接：消失的数字

• 方法1：排序，依次查找，如果下一个数不是上一个数+1，那么上一个数+1就是消失的数字 【O(N*log2(N))】

• 方法2：异或法 【O(N)】

int missingNumber(int* nums, int numsSize)
{
     int x=0;
     for(int i=0;i<numsSize;i++)
     {
         x=x^nums[i];
     }
     for(int i=0;i<numsSize+1;i++)
     {
         x=x^i;
     }
     return x;
}

• 方法3：0~N等差数列求和，再减去数组中已有的数 【O(N)】

int missingNumber(int* nums, int numsSize)
{
    int x = (0 + numsSize) * (numsSize + 1) / 2; //等差数列求和
    for (int i = 0; i < numsSize; i++)
    {
        x = x - nums[i];
    }
    return x; //缺失的数=等差数列的和-数组中已有的数
}

2、空间复杂度

• 空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用额外存储空间大小的量度
• 空间复杂度不是程序占用了多少bytes的空间，空间复杂度算的是变量的个数
• 注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定

（1）冒泡排序O(1)

（2）斐波那契递归O(N)

（3）阶乘递归O(N)

（4）Leetcode题目链接：轮转数组

void swap(int* a, int* b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

void reverse(int arr[], int start, int end)
{
    while (start < end)
    {
        swap(&arr[start], &arr[end]);
        start++;
        end--;
    }
}

void rotate(int* nums, int numsSize, int k)
{
    //方法一：
    // int temp=0;
    // for(int i=0;i<k;i++)
    // {
    //     temp=nums [numsSize-1];
    //     for(int j=numsSize-1;j>0;j--)
    //     {
    //         nums[j]=nums[j-1];
    //     }
    //     nums[0]=temp;
    // }

    //方法二：
    // int newArr[numsSize];
    // for (int i = 0; i < numsSize; i++)
    // {
    //     newArr[(i + k) % numsSize] = nums[i];
    // }
    // for (int i = 0; i < numsSize; i++)
    // {
    //     nums[i] = newArr[i];
    // }

    //方法三：
    k = k % numsSize; //k可能比数组大，在这种情况下，向右移动整个数组长度后就回到原来的位置，k%numsSize就是去掉每次回到原来位置的步数，获得能够产生相同结果的最少步数
    reverse(nums, 0, numsSize - 1);
    reverse(nums, 0, k - 1);
    reverse(nums, k, numsSize - 1);
}