LeetCode：28. 找出字符串中第一个匹配项的下标 ——【1、理解 KMP 算法】网站首页 技术交流

LeetCode：28. 找出字符串中第一个匹配项的下标 ——【1、理解 KMP 算法】

Super algorithm 2023-05-22 09:01:49

简介LeetCode：28. 找出字符串中第一个匹配项的下标 ——【1、理解 KMP 算法】

🍎道阻且长，行则将至。🍓

🌻算法，不如说它是一种思考方式🍀

算法专栏： 👉🏻123

一、🌱28. 找出字符串中第一个匹配项的下标

题目描述：给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。
来源：力扣（LeetCode）
难度：中等
提示：
1 <= haystack.length, needle.length <= 10⁴
haystack 和 needle 仅由小写英文字符组成

🌴解题

1.暴力法

暴力法只需要判断字符串 A 的子字符串和目标字符串 needle 是不是相等即可；
用 i 遍历与目标字符串等长的 A 的子字符串：haystack.substring(i,i+needle.length()) ==needle
注意到，这个遍历并不需要到字符串 A 的结尾，因为匹配长度的原因，遍历区间是 [0，haystack.length()-needle.length()]。

code：

class Solution {
    public int strStr(String haystack, String needle) {
        int ans=-1;
        for (int i = 0; i <= haystack.length()-needle.length(); i++) {
            if(haystack.substring(i,i+needle.length()).equals(needle)){
                return i;
            }
        }
        return ans;
    }
}

在这里插入图片描述

2.模式串匹配

KMP 算法

在前面使用暴力法匹配的时候是浪费了很多的匹配次数，就是指有一部分内容可以略过，不用从头开始：
在这里插入图片描述
例如上图中，遍历到第 7 个字符匹配 (b - c) 的时候，发现是不匹配的。按常规方法来说又得从字符串 A 第 2 个字符及目标第一个字符开始往后面遍历，而实际上在 a b a 这一段开始的匹配是做的无用功，而有用的就是 (b - c) 前面匹配过的 a a：
字符串 A 中的b前面的 a a（红框里）可以匹配上目标最前面的 a a ，字符串A的遍历就不必要回头，只有目标要返回；
例如下图：
在这里插入图片描述

即：找到目标串最前面和最后面相同的字串，这一部分不用重复，是已经验证过的。

有了前面的理解，我们就可以更好理解 KMP 算法了。
KMP 中的模式串就是目标字符串，而模式串(目标)如何回头——使用 next 数组，或说前缀表，来确定模式串的指针回到哪个位置。

前缀表就是记录一个最长公共前后缀，
前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串；
就是前缀==后缀的一个长度。

例如对于这个模式(目标)串，最长公共前后缀：
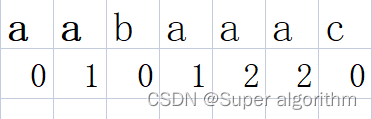
在这里插入图片描述

对于a：没有最长公共前后缀——0；
对于aa：第一个a和最后一个a——1；
对于aab：第一个a和最后一个b，不匹配——0；
对于aaba：第一个a和最后一个a——1；
对于aabaa：前面的aa和最后的aa——2，注意aab和baa、aaba和abaa不是相等的；
…
那我们理解了这个概念，又如何用代码实现求 next 数组呢？

int[] next=new int[needle.length()];
int j=0;
next[j]=0;
for (int i = 1; i < needle.length(); i++) {
    while(j>0&&needle.charAt(j)!=needle.charAt(i)){
        j=next[j-1];
    }
    if(needle.charAt(j)==needle.charAt(i)){
        j++;
    }
    next[i]=j;
}

求 next 数组演示图：
在这里插入图片描述
根据 next 数组模式匹配：

code：

class Solution {
    public int strStr(String haystack, String needle) {
        int ans=-1;
        //计算前缀和next数组
        int[] next=new int[needle.length()];
        int j=0;
        next[j]=0;
        for (int i = 1; i < needle.length(); i++) {
            while(j>0&&needle.charAt(j)!=needle.charAt(i)){
                j=next[j-1];
            }
            if(needle.charAt(j)==needle.charAt(i)){
                j++;
            }
            next[i]=j;
        }

        //匹配
        j=0;
        for (int i = 0; i < haystack.length(); i++) {
            if(j< needle.length()) {
                if (haystack.charAt(i) == needle.charAt(j)) {
                    j++;
                } else if(j>0){
                    j = next[j - 1];
                    i--;
                }
            }
            if(j== needle.length()){
                ans=i-needle.length()+1;
                break;
            }
        }

        return ans;

    }
}