【数据结构】---二叉树类型部分练习解析让你更深程度了解二叉树网站首页 技术交流

【数据结构】---二叉树类型部分练习解析让你更深程度了解二叉树

小沈熬夜秃头中୧⍤⃝❅ 2024-07-23 06:01:02

简介【数据结构】---二叉树类型部分练习解析让你更深程度了解二叉树

文章目录

前言
?一、第一种：二叉树性质类型：
?二、第二种：二叉树遍历+创建类型：
?总结

前言

?个人主页：@小沈熬夜秃头中୧⍤⃝❅
?小编介绍：欢迎来到我的乱七八糟小星球?
?专栏：数据结构
?本章内容：二叉树类型部分练习
送给各位?：月亮本无光努力久了便会万丈光芒
记得评论? +点赞? +收藏? +关注?哦~

提示：以下是本篇文章正文内容，下面案例可供参考

?一、第一种：二叉树性质类型：

二叉树性质:

若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2(i-1)个结点.
若规定根节点的层数为1，则深度为h的二叉树的最大结点数是 2h -1.
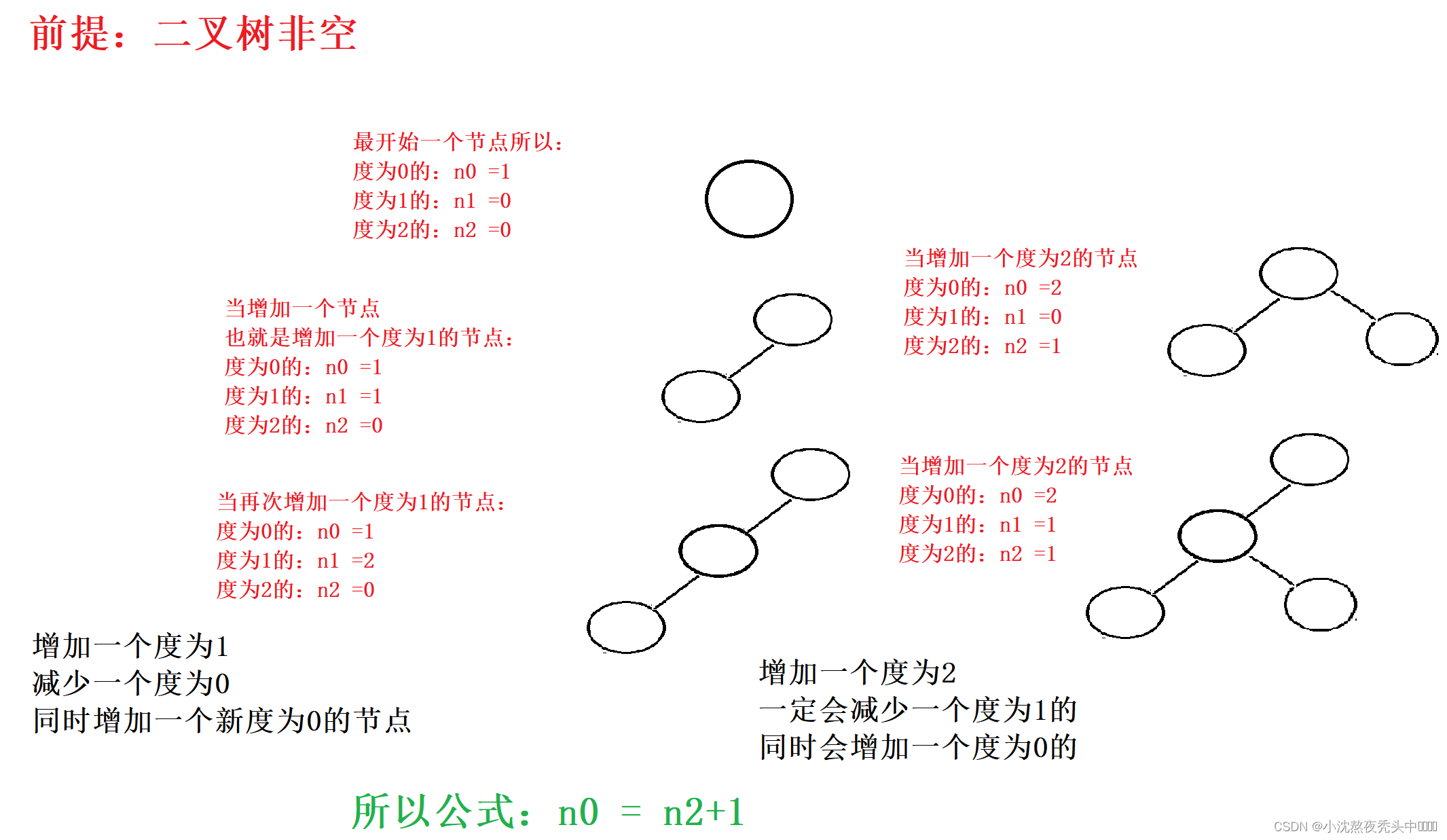
对任何一棵二叉树, 如果度为0其叶结点个数为 n, 度为2的分支结点个数为m ,则有n ＝m＋1
若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=log2(n+1) . (ps：log2(n+1)是log以2为底，n+1为对数)
对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有:
若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

***具体可看***：【数据结构】— 博主拍了拍你并向你扔了一“棵”二叉树(概念+结构)

?1.1 第一题：

某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（***B***）
A 不存在这样的二叉树
B 200
C 198
D 199

?1.1.1 理论：

***关于二叉树的度具体可看***：【数据结构】— 博主拍了拍你并向你扔了一“棵”二叉树(概念+结构)

节点的度：一个节点含有的子树的个数称为该节点的度；如上图：A的为6：B C D E F G

?1.1.2 图解：

?1.1.3 解析：

某二叉树共有 399 个结点，其中有 199 个度为 2 的结点(n2)，则该二叉树中的叶子结点数(n0)为
这就相当于知道了度为2的让你度为1的代入公式：n0=n2+1 <==> n0=199+1<=>20

?1.2 第二题：

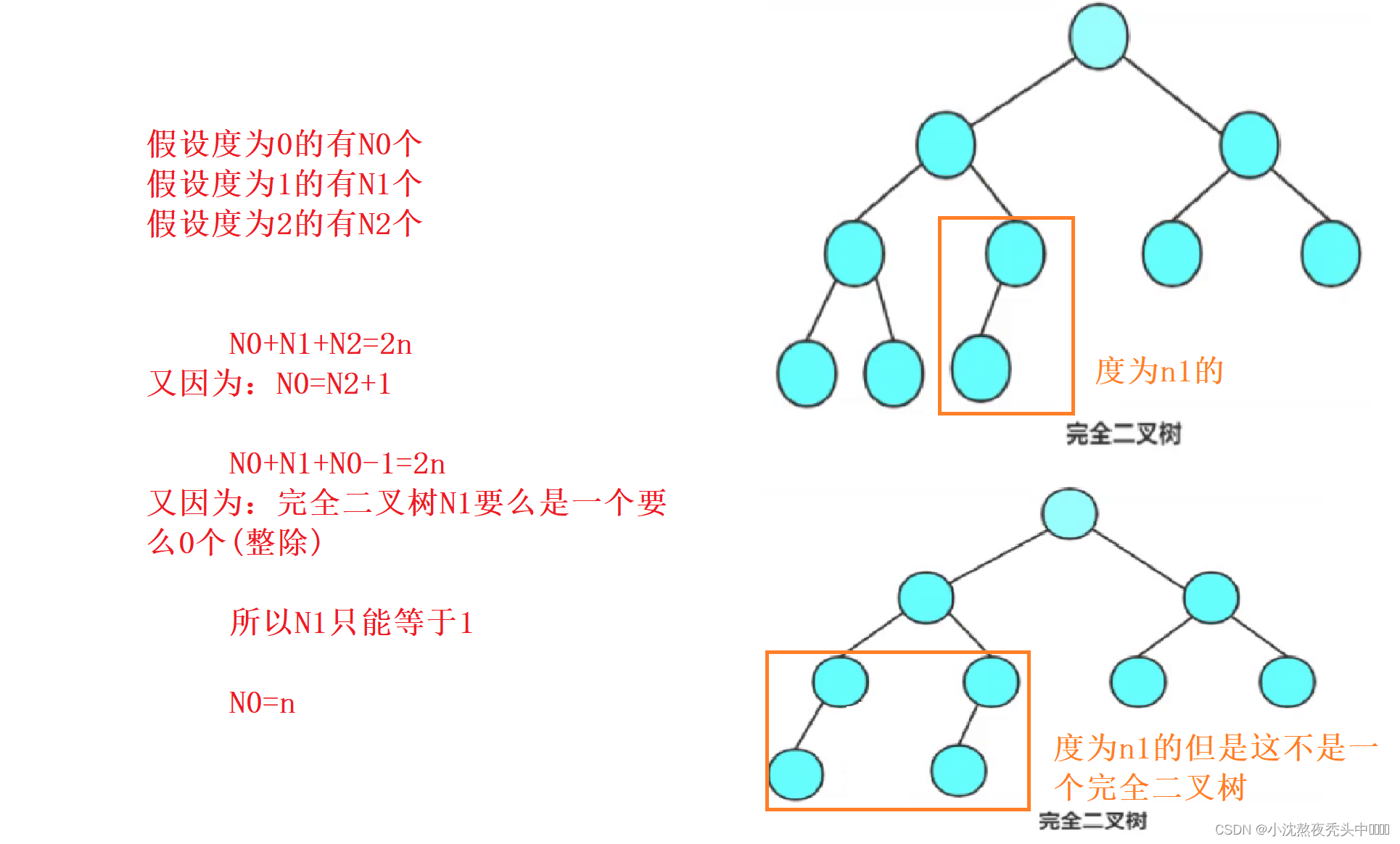
在具有 2n 个结点的完全二叉树中，叶子结点个数为（***A***）
A n
B n+1
C n-1
D n/2

?1.2.1 理论：

完全二叉树度为1的节点个数最多有一个，最少有0个

?1.2.2 图解：

?1.3 第三题：

一棵完全二叉树的节点数位为531个，那么这棵树的高度为（***B***）
A 11
B 10
C 8
D 12

?1.3.1 理论推理：

高度为h的满二叉树的节点数量：2^h-1
***具体推论可以看：***【数据结构】— 博主拍了拍你并向你扔了一“棵”二叉树(概念+结构)
排除法带入可以算出带入10是可以满足的算出大致范围是[512 1023]
512(代表前9层是满的然后第十层有一个所以2^9-1+1 == 512)
1023(代表满二叉树2^10-1=1024)

?二、第二种：二叉树遍历+创建类型：

?2.1 牛客题目：

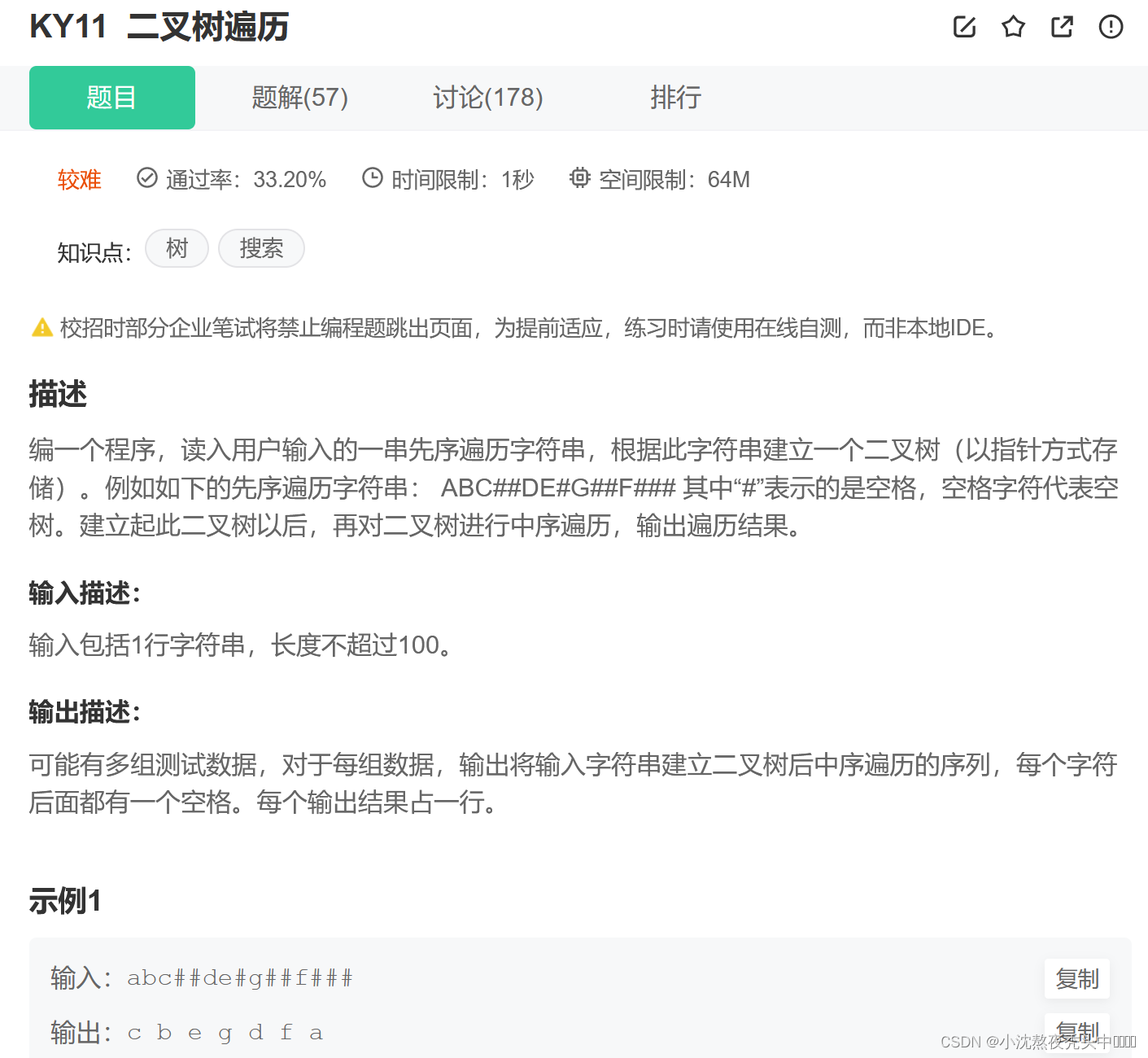
? 题目：KY11 二叉树遍历

描述
编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。
输入描述：
输入包括1行字符串，长度不超过100。
输出描述：
可能有多组测试数据，对于每组数据，输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。每个输出结果占一行。

?2.2 链接：

KY11 二叉树遍历

?2.3 代码：

对于为什么传i的地址而不是传值可以看力扣—二叉树OJ题(多种题型二叉树)

#include <stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}
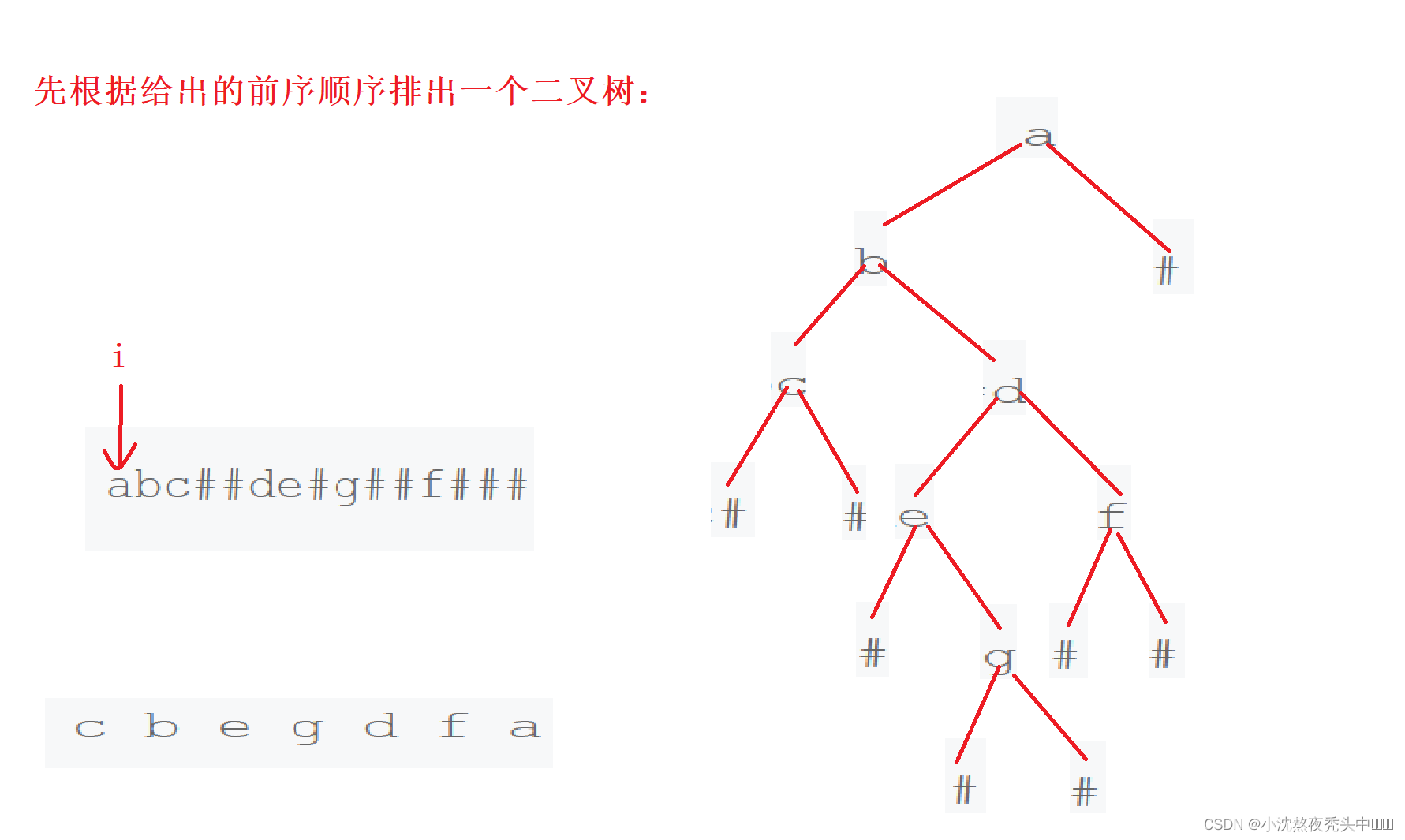
BTNode* CreatTree(char* a,int* pi)
{
    if(a[*pi]=='#')
    {
        (*pi)++;
        return NULL;
    }
    BTNode* root=BuyNode(a[*pi]);
    (*pi)++;
    root->left=CreatTree(a,pi);
    root->right=CreatTree(a,pi);
    return root;
}
void InOrder(BTNode* root)
{
    if(root==NULL)
    return;
    InOrder(root->left);
    printf("%c ",root->data);
    InOrder(root->right);
}
int main() 
{
    int i=0;
    char a[100];
    scanf("%s",a);
    BTNode* root=CreatTree(a,&i);
    InOrder(root);
    return 0;
}