您现在的位置是:首页 >学无止境 >【动态规划】通配符匹配与正则表达式匹配网站首页学无止境
【动态规划】通配符匹配与正则表达式匹配
一、通配符匹配
题目描述:
给你一个输入字符串 (s) 和一个字符模式 § ,请你实现一个支持 ‘?’ 和 ‘*’ 匹配规则的通配符匹配:
- ‘?’ 可以匹配任何单个字符。
- ‘*’ 可以匹配任意字符序列(包括空字符序列)。
判定匹配成功的充要条件是:字符模式必须能够 完全匹配 输入字符串(而不是部分匹配)。
示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:s = “aa”, p = ""
输出:true
解释:'’ 可以匹配任意字符串。
示例 3:
输入:s = “cb”, p = “?a”
输出:false
解释:‘?’ 可以匹配 ‘c’, 但第二个 ‘a’ 无法匹配 ‘b’。
1.1 思路分析
我们可以分别以i和j表示s[0~i]和p[0~j]是否能成功匹配。
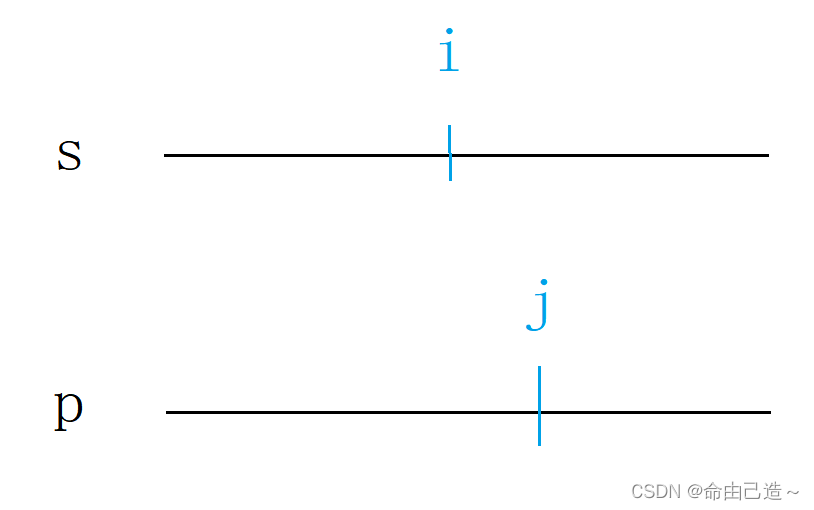
那么这里就只用讨论i和j的位置,有四种情况:
1️⃣ 如果s[i] == p[j],那么我们就只用判断dp[i - 1][j - 1]是否能成功匹配,如果能成功匹配,那么说明加上i和j的位置也能成功匹配。
状态转移方程:dp[i][j] = s[i] == p[j] && dp[i - 1][j - 1]
2️⃣ 如果p[j] == '?'那么说明此时s[i]不管是什么都可以,只需要判断dp[i - 1][j - 1]是否能成功匹配,就跟上面一样。
状态转移方程:dp[i][j] = p[j] == '?' && dp[i - 1][j - 1]
3️⃣ 如果p[j] == '*',这里的情况就比较多,因为它可以变成0个或多个字符:
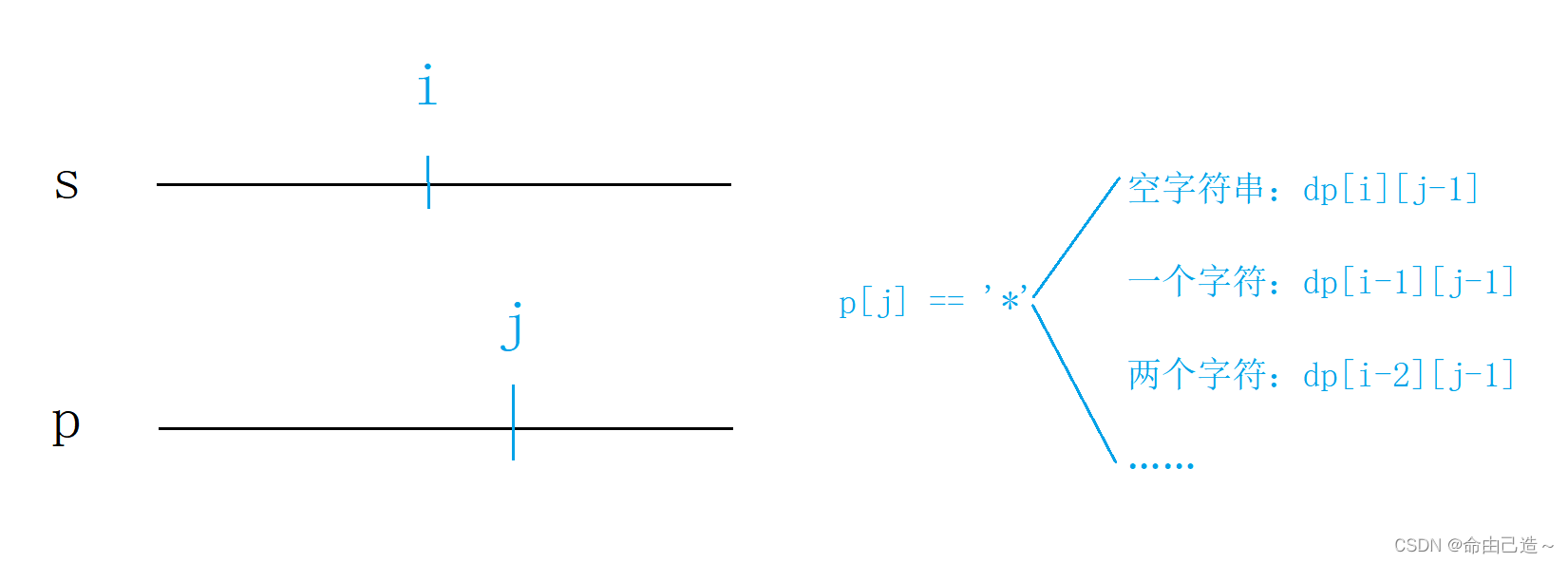
这么多情况只要有一种情况满足条件即可。
状态转移方程:
for(int k = 0; k <= i; k++)
{
if(dp[i - k][j - 1])
{
dp[i][j] = true;
break;
}
}
4️⃣ 如果p[j] != '?' && p[j] != '*' && p[j] != s[i],那么说明不能匹配。
1.2 初始化处理
我们看到状态转移方程会用到i-1和j- 1,所以dp表可以多开一维,而为了不改变下标的映射关系,我们可以在s串和p串的开头各自添加一个字符。
接下来就是初始化,首先dp[0][0]就代表两个空串,一定能匹配。所以dp[0][0] = true;
其次还有*在p串开头的位置出现,因为*可以变成空串,所以只要是开头的*都可以跟s[0]匹配成功:dp[0][j] = true;
1.3 代码
class Solution {
public:
bool isMatch(string s, string p) {
s = " " + s;
p = " " + p;
int n = s.size(), m = p.size();
vector<vector<bool>> dp(n, vector<bool>(m));
dp[0][0] = true;
for(int j = 1; j < m; j++)
{
if(p[j] == '*')
{
dp[0][j] = true;
}
else break;
}
for(int i = 1; i < n; i++)
{
for(int j = 1; j < m; j++)
{
if((p[j] == '?' && dp[i - 1][j - 1]))
{
dp[i][j] = true;
}
else if(s[i] == p[j] && dp[i - 1][j - 1])
{
dp[i][j] = true;
}
else if(p[j] == '*')
{
for(int k = 0; k <= i; k++)
{
if(dp[i - k][j - 1])
{
dp[i][j] = true;
break;
}
}
}
}
}
return dp[n - 1][m - 1];
}
};
1.4 优化
p[j] == '*'这种情况其实可以写成:
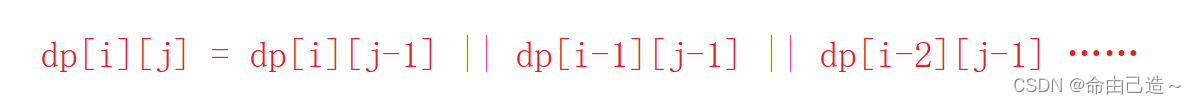
而经过观察可以再写出一个式子:
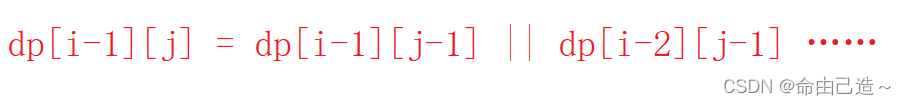
经过观察可以发现蓝色框框圈起来的部分是相等的

所以可以写成:
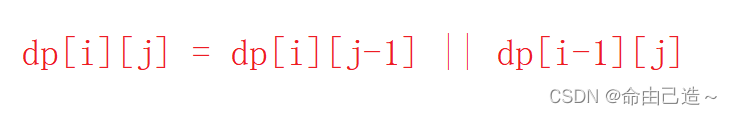
class Solution {
public:
bool isMatch(string s, string p) {
s = " " + s;
p = " " + p;
int n = s.size(), m = p.size();
vector<vector<bool>> dp(n, vector<bool>(m));
dp[0][0] = true;
for(int j = 1; j < m; j++)
{
if(p[j] == '*') dp[0][j] = true;
else break;
}
for(int i = 1; i < n; i++)
{
for(int j = 1; j < m; j++)
{
if(dp[i - 1][j - 1] && (p[j] == '?' || s[i] == p[j])) dp[i][j] = true;
else if(p[j] == '*')
{
dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
}
}
}
return dp[n - 1][m - 1];
}
};
二、正则表达式匹配
题目描述:
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
- ‘.’ 匹配任意单个字符
- ‘*’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:s = “aa”, p = “a*”
输出:true
解释:因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:
输入:s = “ab”, p = “."
输出:true
解释:".” 表示可匹配零个或多个(‘*’)任意字符(‘.’)。
这里的.字符跟上面一道题的?作用是一样的。但是*字符又区别,它的作用是把*字符的前一个字符重复0次或者多次,比方说"a*"
它可以变成:"","a","aa","aaa"……
2.1 思路分析
这里的有些情况跟上面的重复:
当dp[i - 1][j - 1] && (p[j] == '.' || s[i] == p[j])的时候,dp[i][j]=true。
接下来只剩p[j] == '*' 的情况:
这里要分情况讨论j的前一个元素,如果前一个元素是.,那么也就是可以变成任意的多个字符,既然要匹配多个字符,那么又是跟上面一个题一样要讨论到底变成多长。因为上面讲过优化版,所以这里直接写:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TjgwHLLy-1685717763933)(null)]](https://img-blog.csdnimg.cn/86849bfae0e94f9a8de540034d69f0f9.png)
接下来如果前面一个字符是普通字符:
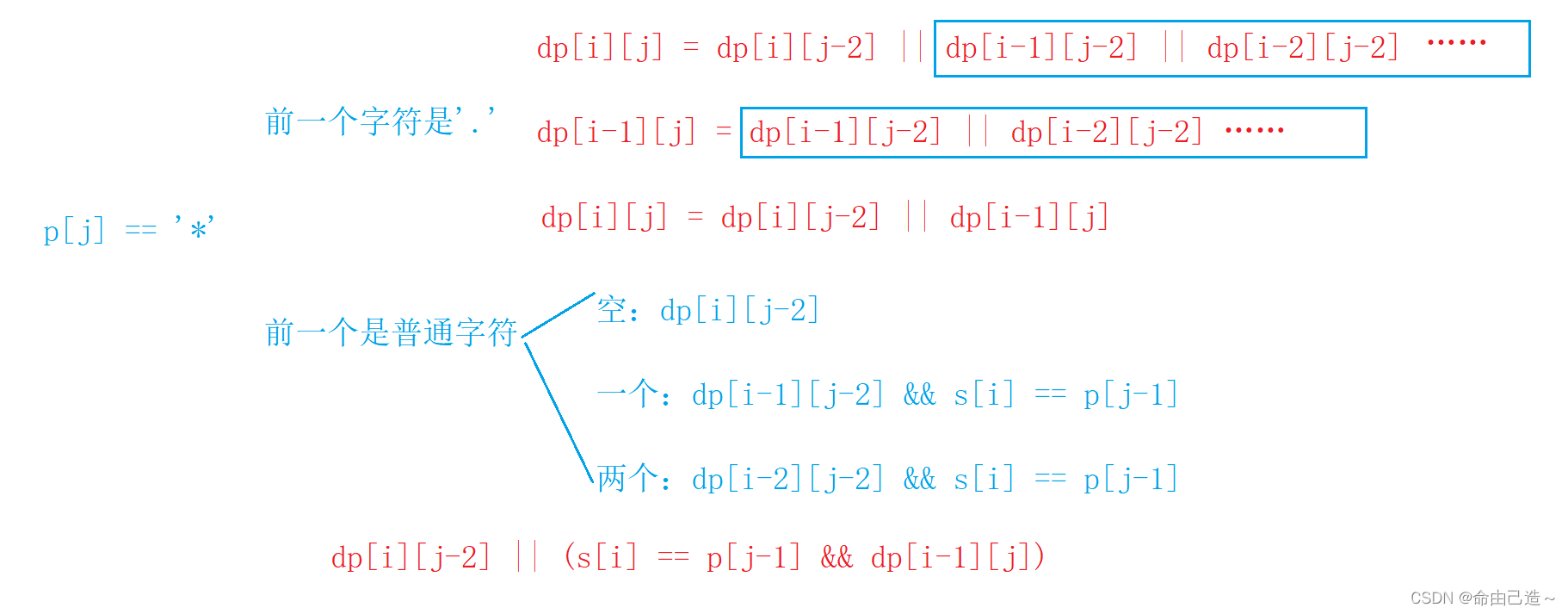
这里解释以下:空自然不用说,当只变成长度为1的字符串时,首先要判断j的前一个字符是否等于s[i],如果不相等就不用考虑前面的了。
2.2 初始化设置
还是跟上面一样多加一维,然后让dp[0][0] = true,接下来就是看p的前面全部是x*x*……这种字符串的情况:
for(int j = 2; j < m; j += 2)
{
if(p[j] == '*') dp[0][j] = true;
else break;
}
2.3 代码
class Solution {
public:
bool isMatch(string s, string p) {
s = " " + s;
p = " " + p;
int n = s.size(), m = p.size();
vector<vector<bool>> dp(n, vector<bool>(m + 1));
dp[0][0] = true;
for(int j = 2; j < m; j += 2)
{
if(p[j] == '*') dp[0][j] = true;
else break;
}
for(int i = 1; i < n; i++)
{
for(int j = 1; j < m; j++)
{
if(p[j] == '*')
{
if(p[j - 1] == '.')
{
dp[i][j] = dp[i][j - 2] || dp[i - 1][j];
}
else
{
dp[i][j] = dp[i][j - 2] || (s[i] == p[j - 1] && dp[i - 1][j]);
}
}
else
{
dp[i][j] = dp[i - 1][j - 1] && (p[j] == '.' || s[i] == p[j]);
}
}
}
return dp[n - 1][m - 1];
}
};






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结