您现在的位置是：首页 >学无止境 >常见的五种排序网站首页学无止境

?博主主页：@ᰔᩚ. 一怀明月ꦿ 

❤️‍?专栏系列：线性代数，C初学者入门训练，题解C，C的使用文章，「初学」C++

?座右铭：“不要等到什么都没有了，才下定决心去做”

???大家觉不错的话，就恳求大家点点关注，点点小爱心，指点指点???

目录

冒泡排序 

选择排序 

插入排序

堆排序

希尔排序

五种排序的效率比较 

冒泡排序 

从左到右，相邻元素进行比较。每次比较之后，就会找到待排数据中最大的一个或者最小的一个，这个数就会从待排数据的最右边冒出来。
以从升序为例，第一次比较后，所有数中最大的那个数就会浮到最右边；第二轮比较后，所有数中第二大的那个数就会浮到倒数第二个位置……就这样一轮一轮地比较，最后实现从小到大排序。

 这里所有排序都以升序为例

//升序
#include<stdio.h>
void Print(int arr[],int len)
{
    for(int i=0;i<len;i++)
    {
        printf("%d ",arr[i]);
    }
    printf("
");
}
void Buble_sort(int arr[],int len)
{
    for(int i=0;i<len-1;i++)
    {
        for(int j=0;j<len-i-1;j++)
        {
            if(arr[j]>arr[j+1])
            {
                int temp=arr[j];
                arr[j]=arr[j+1];
                arr[j+1]=temp;
            }
        }
    }
    Print(arr,len);
}
int main()
{
    int arr[]={9,8,7,6,0,5,4,3,2,1};
    int len=sizeof(arr)/sizeof(*arr);
    Buble_sort(arr,len);
    return 0;
}

结果：0 1 2 3 4 5 6 7 8 9

选择排序 

 选择排序（Choose sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的中数据元素选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

//升序
#include<stdio.h>
void Print(int arr[],int len)
{
    for(int i=0;i<len;i++)
    {
        printf("%d ",arr[i]);
    }
    printf("
");
}
void Choose_sort(int arr[],int len)
{
    for(int i=0;i<len;i++)
    {
        for(int j=i+1;j<len;j++)
        {
            if(arr[i]>arr[j])
            {
                int temp=arr[j];
                arr[j]=arr[i];
                arr[i]=temp;
            }
        }
    }
    Print(arr,len);
}
int main()
{
    int arr[]={9,8,7,6,0,5,4,3,2,1};
    int len=sizeof(arr)/sizeof(*arr);
    Choose_sort(arr,len);
    return 0;
}

结果：0 1 2 3 4 5 6 7 8 9

插入排序

将待排序序列分为两部分，一部分有序一部分无序，我们把第一个元素看作有序序列，从第二个元素到最后为无序序列，将无序序列中每一个元素依次插入到有序序列的合适位置–从小到大（从大到小）。 

#include<stdio.h>
void Print(int arr[],int len)
{
    for(int i=0;i<len;i++)
    {
        printf("%d ",arr[i]);
    }
    printf("
");
}
void Insert_sort(int arr[],int len)
{
    int i,j;
    for( i=0;i<len;i++)
    {
        int temp=arr[i];
        for( j=i-1;j>=0;j--)
        {
            if(temp<arr[j])
            {
                arr[j+1]=arr[j];
            }
            else
            {
                break;
            }
        }
        arr[j+1]=temp;
    }
    Print(arr,len);
}
int main()
{
    int arr[]={9,8,7,6,0,5,4,3,2,1};
    int len=sizeof(arr)/sizeof(*arr);
    Insert_sort(arr,len);
    return 0;
}

结果：0 1 2 3 4 5 6 7 8 9

堆排序

堆排序（HeapSort）就是利用堆（一种数据结构，如果不了解堆，可以看我前面文章了解一下堆）进行排序的方法 。基本思想：将待排序的序列构造成一个大根堆。此时，整个序列的最大值就是堆顶的根结点。将它移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值），然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次小值。如此反复执行，就能得到一个有序序列 
 

主要步骤：建堆（大根堆），调整（向下调整）

#include<stdio.h>
//两数交换
void Swap(int* e1,int* e2)
{
    int temp=*e1;
    *e1=*e2;
    *e2=temp;
}
//向上调整
void AdjustUP(int* a,int n)
{
    int child=n-1;
    int parent=(child-1)/2;
    while(child>0)
    {
        if(a[child]<a[parent])
        {
            Swap(&a[child], &a[parent]);
            child=parent;
            parent=(child-1)/2;
        }
        else
        {
            break;
        }
    }
}
//向下调整
void AdjustDown(int* a,int n,int parent)
{
    int child=parent*2+1;
    while(child<n)
    {
        if(child+1<n&&a[child]<a[child+1])
        {
            child++;
        }
        if(a[child]>a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent=child;
            child=parent*2+1;
        }
        else
        {
            break;
        }
    }
}
//向上建堆排序
//时间复杂度为O(N*logN)
void HeapSort_UP(int* a,int n)
{
    //向上建堆是从第二层开始直到第h层，所以其时间复杂度为O(N*logN)
    for(int i=1;i<n;i++)
    {
        AdjustUP(a, i);
    }
    int end=n-1;
    //建堆完成后，需要进行向下调整其时间复杂度为O(N*logN)
    while(end>0)
    {
        Swap(&a[0], &a[end]);
        AdjustDown(a, end,0);
        end--;
    }
}
//向下建堆排序
//时间复杂度为N*logN
void HeapSort_Down(int* a,int n)
{
    //向下建堆是从第h-1层直到第一层，所以其时间复杂度为O(N)
    for(int i=(n-1-1)/2;i>=0;i--)
    {
        AdjustDown(a, n,i);
    }
    int end=n-1;
    //建堆完成后，需要进行向下调整其时间复杂度为O(N*logN)
    while(end>0)
    {
        Swap(&a[0], &a[end]);
        AdjustDown(a, end,0);
        end--;
    }
}
总结：向上建堆从第二层开始直到第h层，向下建堆是从第h-1层直到第一层，虽然它们经历的层数相同，但是向上建堆中第一层不用调整，向下建堆中第h层不用调整（h为最后一层），第一层的元素只有一个，第h层元素有2^(h-1)个。所以他们的时间复杂度不同，向上建堆为O(N*logN)，向下建堆为O(N)
int main()
{
    int a[]={1,3,5,7,9,0,8,6,4,2};
    int n=sizeof(a)/sizeof(a[0]);
    //HeapSort_UP(a,n);
    HeapSort_Down(a, n);
    for(int i=0;i<n;i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}
//结果：0 1 2 3 4 5 6 7 8 9
结果：0 1 2 3 4 5 6 7 8 9  

希尔排序

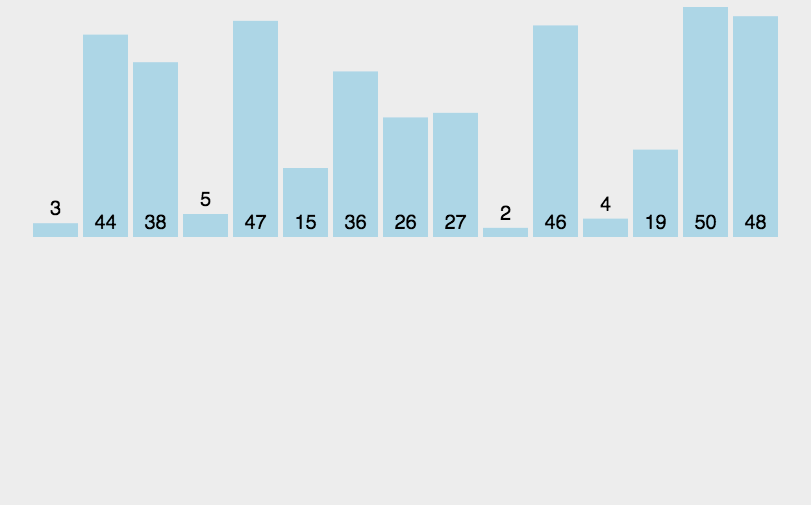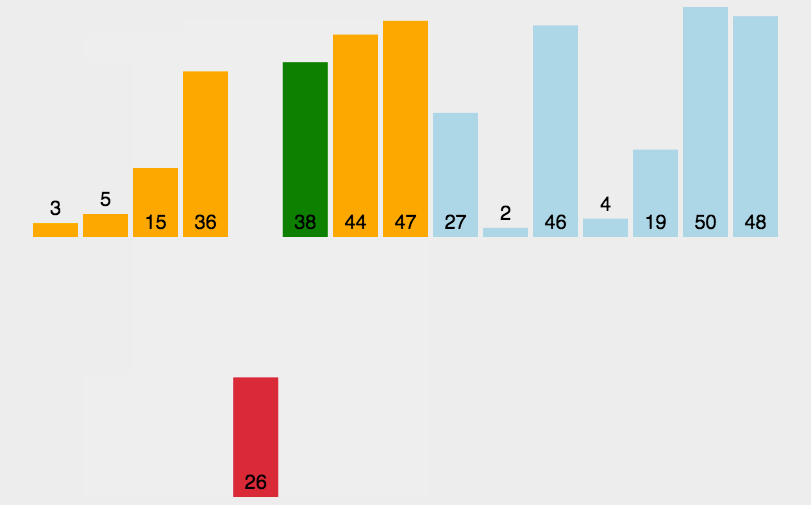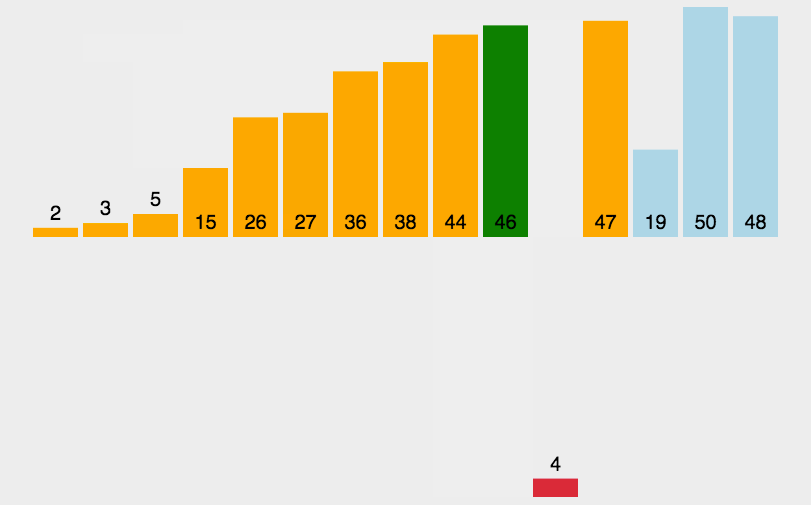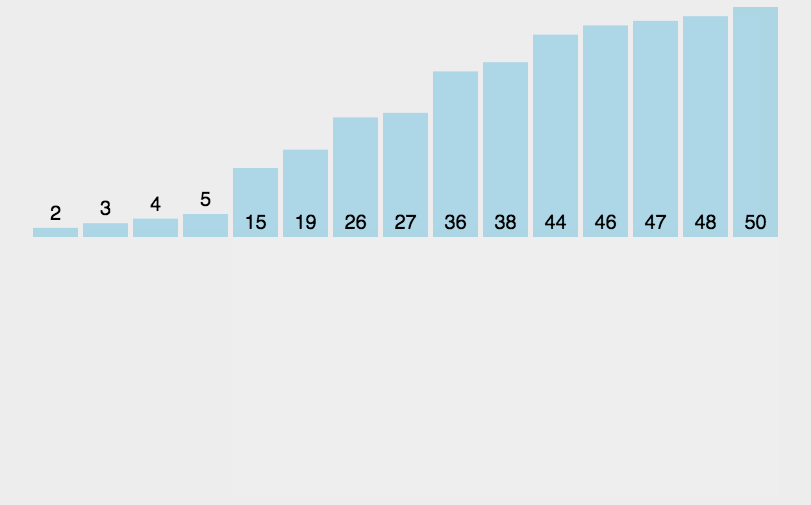
 希尔排序是对插入排序进行优化，希尔排序先选定一个数值（整数）作为增量，把待排序所有数据分为若干组，以每个距离（这个距离就是增量）的等差数列为一组，对每一组进行排序，这一步叫作预排序，然后将增量缩小，继续分组排序，重复上述动作，直到增量缩小为1时，排序完正好有序。

​ 希尔排序原理是每一对分组进行排序后，整个数据就会更接近有序，当增量缩小为1时，就是插入排序，但是现在的数组非常接近有序，移动的数据很少，所以效率非常高，所以希尔排序又叫减小增量排序。

​ 每次排序让数组接近有序的过程叫做预排序，最后一次插入是直接插入排序

希尔排序
1.预排序--接近有序
2.插入排序

间隔gap分为一组，总计gap组
假设gap==3；
预排序：对gap组数据分别进行插入排序


gap越大，大的数可以更快到后面，小的数
#include<stdio.h>
void Print(int* a,int n)
{
    for(int i=0;i<n;i++)
    {
        printf("%d ",a[i]);
    }
    printf("
");
}
归纳公式：合计gap组，每组n/gap个
每组：1+2+3+...+n/gap
合集gap组
总计：gap*(1+2+3+...+n/gap)

O(N^1.33)
int main()
{
    int a[]={9,8,7,6,5,4,3,2,1,0};
    int n=sizeof(a)/sizeof(*a);
    int gap=n;
    while(gap>1)//时间复杂度log3^N
    {
        gap=gap/3+1;
//        for(int j=0;j<n-gap;j++)
//        {
            for(int i=0;i<n-gap;i++)//N
            {
                int end=i;
                int temp=a[end+gap];
                while(end>=0)//log3^N
                {
                    if(a[end]>temp)
                    {
                        a[end+gap]=a[end];
                        end-=gap;
                    }
                    else
                    {
                        break;
                    }
                }
                a[end+gap]=temp;
            }
//        }
    }
    Print(a, n);
    return 0;
}
结果：0 1 2 3 4 5 6 7 8 9

五种排序的效率比较 

其实这里是六种排序，我在这里加入了 C 语言库里的快速排序qsort，为了更好比较各个排序的效率。这里采用六种排序同时排序具有 相同10000 个数据的数组。

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
//打印函数
void Print(int* a,int n)
{
    for(int i=0;i<n;i++)
    {
        printf("%d ",a[i]);
    }
    printf("
");
}
//交换函数
void Swap(int* e1,int* e2)
{
    int temp=*e1;
    *e1=*e2;
    *e2=temp;
}
//向下调整
//大根堆
void AdjustDown(int* a,int n,int parent)
{
    int child=parent*2+1;
    while(child<n)
    {
        if(child+1<n&&a[child]>a[child+1])
        {
            child++;
        }
        if(a[child]<a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent=child;
            child=parent*2+1;
        }
        else
        {
            break;
        }
    }
}
//建大堆排序
void AdjustDownSort(int*a,int n)
{
    for(int i=(n-1-1)/2;i>=0;i--)
    {
        AdjustDown(a, n, i);
    }
    int end=n-1;
    while(end>0)
    {
        Swap(&a[0], &a[end]);
        AdjustDown(a, end, 0);
        end--;
    }
}
//冒泡排序
void BubbleSort(int* a,int n)
{
    for(int i=0;i<n-1;i++)
    {
        for(int j=0;j<n-i-1;j++)
        {
            if(a[j]>a[j+1])
                Swap(&a[j], &a[j+1]);
        }
    }
}
//选择排序
void SelectSort(int* a,int n)
{
    for(int i=0;i<n;i++)
    {
        for(int j=i+1;j<n;j++)
        {
            if(a[i]>a[j])
                Swap(&a[i], &a[j]);
        }
    }
}
//插入排序
void InsertSort(int* a,int n)
{
    for(int i=0;i<n;i++)
    {
        int end=i;
        int temp=a[i+1];
        while(end>=0)
        {
            if(a[end]>temp)
            {
                a[end+1]=a[end];
                end--;
            }
            else
            {
                break;
            }
        }
        a[end+1]=temp;
    }
}
//希尔排序
void SellSort(int* a,int n)
{
    int gap=n;
    while(gap>1)
    {
        gap=gap/3+1;
        for(int i=0;i<n-gap;i++)
        {
            int end=i;
            int temp=a[end+gap];
            while(end>=0)
            {
                if(a[end]>temp)
                {
                    a[end+gap]=a[end];
                    end-=gap;
                }
                else
                {
                    break;
                }
            }
            a[end+gap]=temp;
        }
    }
}
int cmp_int(const void* e1, const void* e2)
{
 return *(int*)e1 - *(int*)e2;
}


int main()
{
    srand((unsigned int)time(NULL));
    const int N=10000;
    int* a1=(int*)malloc(sizeof(int)*N);
    int* a2=(int*)malloc(sizeof(int)*N);
    int* a3=(int*)malloc(sizeof(int)*N);
    int* a4=(int*)malloc(sizeof(int)*N);
    int* a5=(int*)malloc(sizeof(int)*N);
    int* a6=(int*)malloc(sizeof(int)*N);
    
    for(int i=0;i<N;i++)
    {
        a1[i]=rand()%100;
        a2[i]=a1[i];
        a3[i]=a1[i];
        a4[i]=a1[i];
        a5[i]=a1[i];
        a6[i]=a1[i];
    }
    int begin1=(int)clock();
    BubbleSort(a1, N);
    int end1=(int)clock();
    printf("冒泡排序所需的时间：%dms
",end1-begin1);
    
    int begin2=(int)clock();
    SelectSort(a2, N);
    int end2=(int)clock();
    printf("选择排序所需的时间：%dms
",end2-begin2);
    
    int begin3=(int)clock();
    AdjustDownSort(a3, N);
    int end3=(int)clock();
    printf("堆排序所需的时间：%dms
",end3-begin3);
    
    int begin4=(int)clock();
    InsertSort(a4, N);
    int end4=(int)clock();
    printf("插入排序所需的时间：%dms
",end4-begin4);
    
    int begin5=(int)clock();
    SellSort(a5, N);
    int end5=(int)clock();
    printf("希尔排序所需的时间：%dms
",end5-begin5);
    
    int begin6=(int)clock();
    qsort(a6, N, 4, cmp_int);
    int end6=(int)clock();
    printf("快排排序所需的时间：%dms
",end6-begin6);
    return 0;
}

结果：

泡排序所需的时间：389679ms

选择排序所需的时间：165760ms

堆排序所需的时间：3005ms

插入排序所需的时间：75965ms

希尔排序所需的时间：1628ms

快排排序所需的时间：585ms

可见快排、希尔排序和堆排序是一个量级，其中快排的效率非常高，不可思议的是希尔排序的效率高过了时间效率为O(N*logN)的堆排序，虽然希尔排序的中循环比较多，但是时间效率并不高，因为希尔排序的时间效率存在难以解决的数学难题，所以很难精确其时间效率，希尔排序的时间效率大概是 O(N^1.3)。插入排序、选择排序和冒泡排序，这三种排序的时间效率都为O(N^2)，其中插入排序的效率明显高于其他两个，冒泡排序的效率非常低，没有实际的用途，常用于教学。

  ???如果大家还有不懂或者建议都可以发在评论区，我们共同探讨，共同学习，共同进步。谢谢大家！ ???