您现在的位置是：首页 >其他 >C#，码海拾贝（30）——求“广义逆”的“奇异值分解法SVD”C#源代码，《C#数值计算算法编程》源代码升级改进版网站首页其他

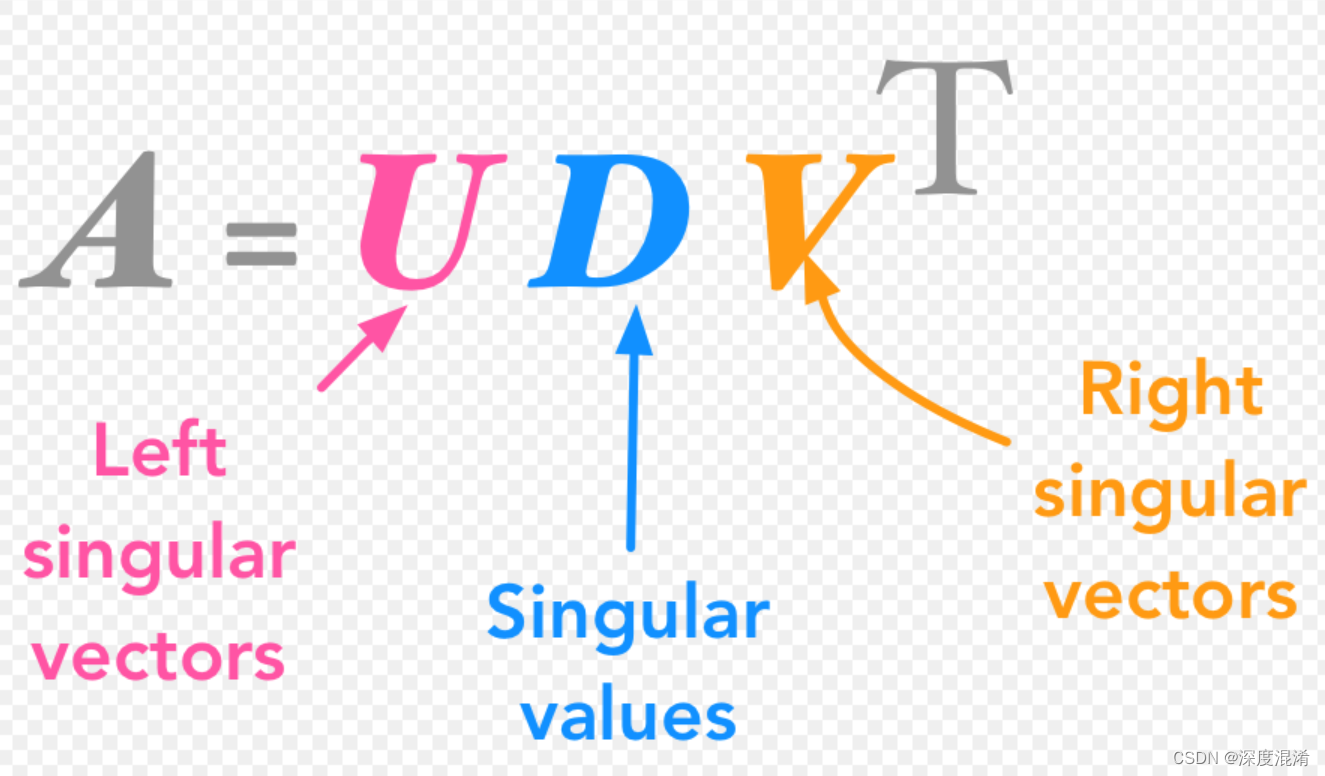
The Singular Value Decomposition (SVD) of a matrix is a factorization of that matrix into three matrices. It has some interesting algebraic properties and conveys important geometrical and theoretical insights about linear transformations. It also has some important applications in data science. In this article, I will try to explain the mathematical intuition behind SVD and its geometrical meaning. 

using System;

namespace Zhou.CSharp.Algorithm
{
    /// <summary>
    /// 矩阵类
    /// 作者：周长发
    /// 改进：深度混淆
    /// https://blog.csdn.net/beijinghorn
    /// </summary>
    public partial class Matrix
    {
        /// <summary>
        /// 求广义逆的奇异值分解法，分解成功后，原矩阵对角线元素就是矩阵的奇异值
        /// </summary>
        /// <param name="src">源矩阵</param>
        /// <param name="mtxAP">原矩阵的广义逆矩阵</param>
        /// <param name="mtxU">分解后的U矩阵</param>
        /// <param name="mtxV">分解后的V矩阵</param>
        /// <param name="eps">计算精度</param>
        /// <returns>求解是否成功</returns>
        public static bool InvertUV(Matrix src, Matrix mtxAP, Matrix mtxU, Matrix mtxV, double eps)
        {
            int i, j, k, u, t, p, q, f;

            // 调用奇异值分解
            if (!SplitUV(src, mtxU, mtxV, eps))
            {
                return false;
            }
            int m = src.Rows;
            int n = src.Columns;

            // 初始化广义逆矩阵
            if (!mtxAP.Init(n, m))
            {
                return false;
            }
            // 计算广义逆矩阵

            j = n;
            if (m < n)
            {
                j = m;
            }
            j = j - 1;
            k = 0;
            while ((k <= j) && Math.Abs(src[k * n + k]) > float.Epsilon)//([k * n + k] != 0.0))
            {
                k = k + 1;
            }
            k = k - 1;
            for (i = 0; i <= n - 1; i++)
            {
                for (j = 0; j <= m - 1; j++)
                {
                    t = i * m + j;
                    mtxAP[t] = 0.0;
                    for (u = 0; u <= k; u++)
                    {
                        f = u * n + i;
                        p = j * m + u;
                        q = u * n + u;
                        mtxAP[t] = mtxAP[t] + mtxV[f] * mtxU[p] / src[q];
                    }
                }
            }

            return true;
        }
    }
}