您现在的位置是：首页 >技术教程 >从C语言到C++_14(vector的常用函数+相关选择题和OJ题)网站首页技术教程
从C语言到C++_14(vector的常用函数+相关选择题和OJ题)
目录
26. 删除有序数组中的重复项 - 力扣（LeetCode）
137. 只出现一次的数字 II - 力扣（LeetCode）
260. 只出现一次的数字 III - 力扣（LeetCode）
剑指 Offer 39. 数组中出现次数超过一半的数字 - 力扣（LeetCode）
剑指 Offer 42. 连续子数组的最大和 - 力扣（LeetCode）
1. vector的常用函数
1.1 vector 的介绍
文档链接：
https://cplusplus.com/reference/vector/vector/
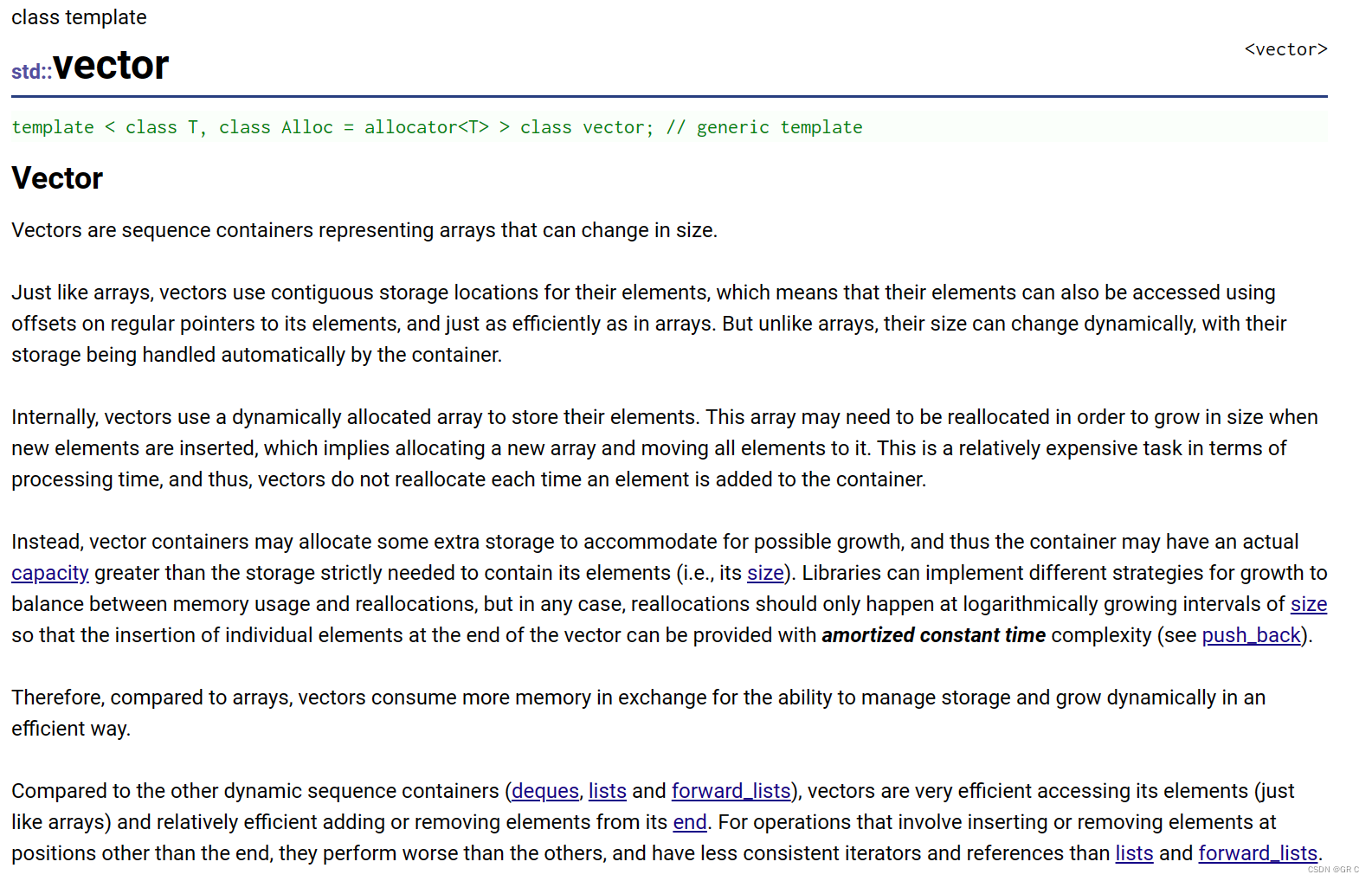
① vector 是表示可变大小数组的序列容器，我们说 vector 像数组，但是又不像数组。
说它像数组体现在：vector 就像是数组一样，它也是采用连续存储空间来存储元素的。这也就意味着我们可以用下标访问 vector 的元素，和数组一样的高效。
说它不像数组体现在：vector 的大小是可以动态改变的，而且它的大小会被容器自动处理。
② 本质上来说，vector 使用动态分配数组来存储它的元素。
当新元素插入时，为了增加存储空间，这个数组就需要被重新分配大小。具体做法是分配一个新的数组，然后将全部元素转移到这个新的数组。就时间而言，这是一个相对代价较高的任务，因为每当一个新的元素加入后，vector 并不会每次都重新分配大小。
③ vector 分配空间策略：vector 会分配一些额外的空间以适应可能的增长，因此存储空间会比实际需要的存储空间更大。不同的库采用不同的策略权衡空间的使用和重新分配。但是无论如何，重新分配都应该是对数增长的间隔大小，以至于末尾插入一个元素时是在常数时间的复杂度完成的。
因此，vector 占用了更多的存储空间，为了获得管理存储空间的能力，并且由一种有效的方式去动态增长。
④ 与其它动态序列容器相比（deques, lists and forward_lists）：
vector 在访问元素的时候更加高效，在末尾添加和删除元素相对高效。 但是对于其它不在末尾的删除和插入操作，效率更低。比起 lists 和 forward_lists 统一的迭代器和引用更好。
vector 的底层就是一个动态的顺序表
1.2 vector 的初始化
vector 是一个类模板，所以需要显示类型转化了：
#include<iostream>
#include<vector>
using namespace std;
int main()
{
vector<int> v1;
vector<int> v2(10, 1);
vector<int> v3(v2);
vector<int> v4(v2.begin(), v2.end());
string str("hello world");
vector<char> v5(str.begin(), str.end());
return 0;
}
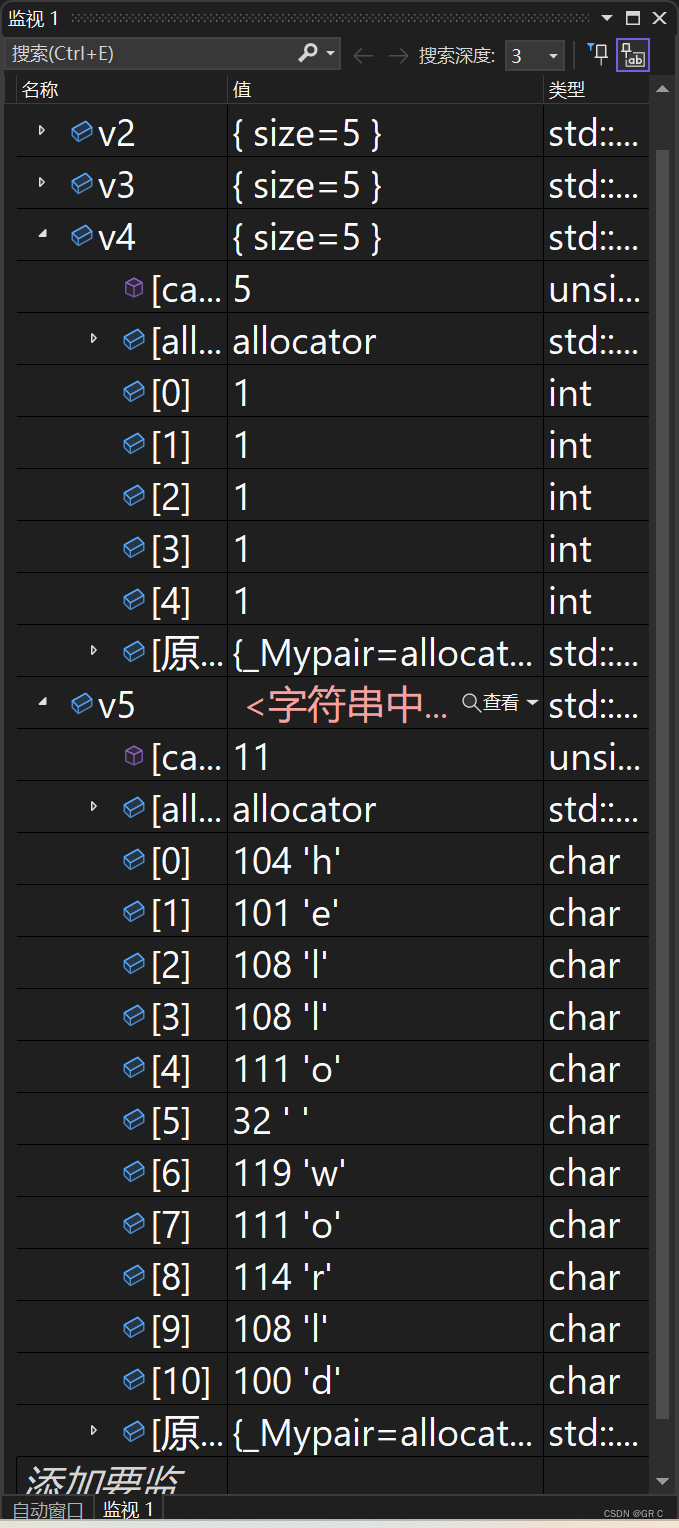
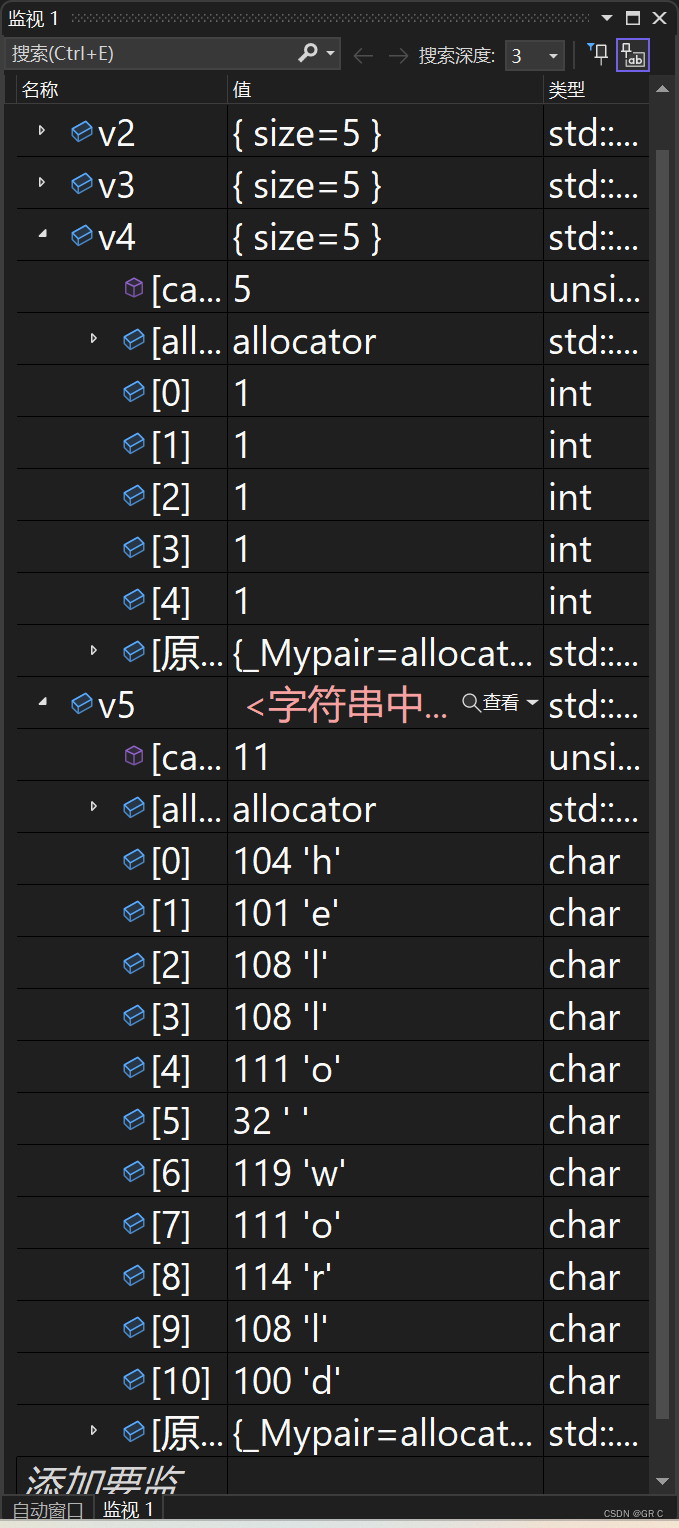
string 和 vector 有什么区别呢？刚才通过监视观察，感觉 vector char 已经很像 string 了。
能不能让 vector char 去替代 string 呢？这合适吗？
答案是否定的。因为 vector char 没有 ，而 string 结尾是有 的。
那我给 vector char 后面手动装一个 行不？
也不是不可以。但是 "术业有专攻" ，他们俩的体系是不一样的。
vector 是顺序表，存的是任意类型，是针对可动态增长的数组的。
vector 支持正常的增删查改，但是不支持 += （本身也没必要+=），也不支持比较大小。
vector 也没有 c_str 这些东西，因为 string 作为字符串专用的类，能提供专有的接口（比如 +=，find），所以这就是 string 存在的意义。
关于析构函数，一般情况下我们不需要管，因为它会自动调用。
拷贝构造和赋值构造，vector 的拷贝构造和赋值其实就是深拷贝。
这些我们放在 vector 模拟实现的章节里详细探讨。
1.3 vector 的操作和遍历
先简单介绍 3 种 vector 的遍历方式，然后再介绍一些访问元素的接口。
其中为了讲解 "下标 + 方括号" 的遍历方式，我们先提前介绍一下 vector 的 push_back 。
除此之外还有反向迭代器、const 迭代器……就不一一介绍了，具体可以看文档。
vector 不能用爽到飞起地 operator+=
string 能用 += 主要是 string 不仅可以尾插一个字符还可以追加一个字符串。
但是 vector 就只支持一个一个数据的插入和删除，push_back 和 pop_back。
vector 的接口和我们在数据结构实现过的顺序表都差不多。
而且学了string 大多都会用了，所以只简单介绍几个，剩下的可以自己查文档。
提一嘴：operator[] 会用断言检查越界，而 at() 会抛异常，平时基本不用at() 的。
vector 和 string 一样，是没有提供 push_front 和 pop_front 的，因为挪动数据效率低。
虽然可以用 insert 和 erase 去操作，但效率确实低，不建议。我们来玩一玩遍历：
#include<iostream>
#include<vector>
using namespace std;
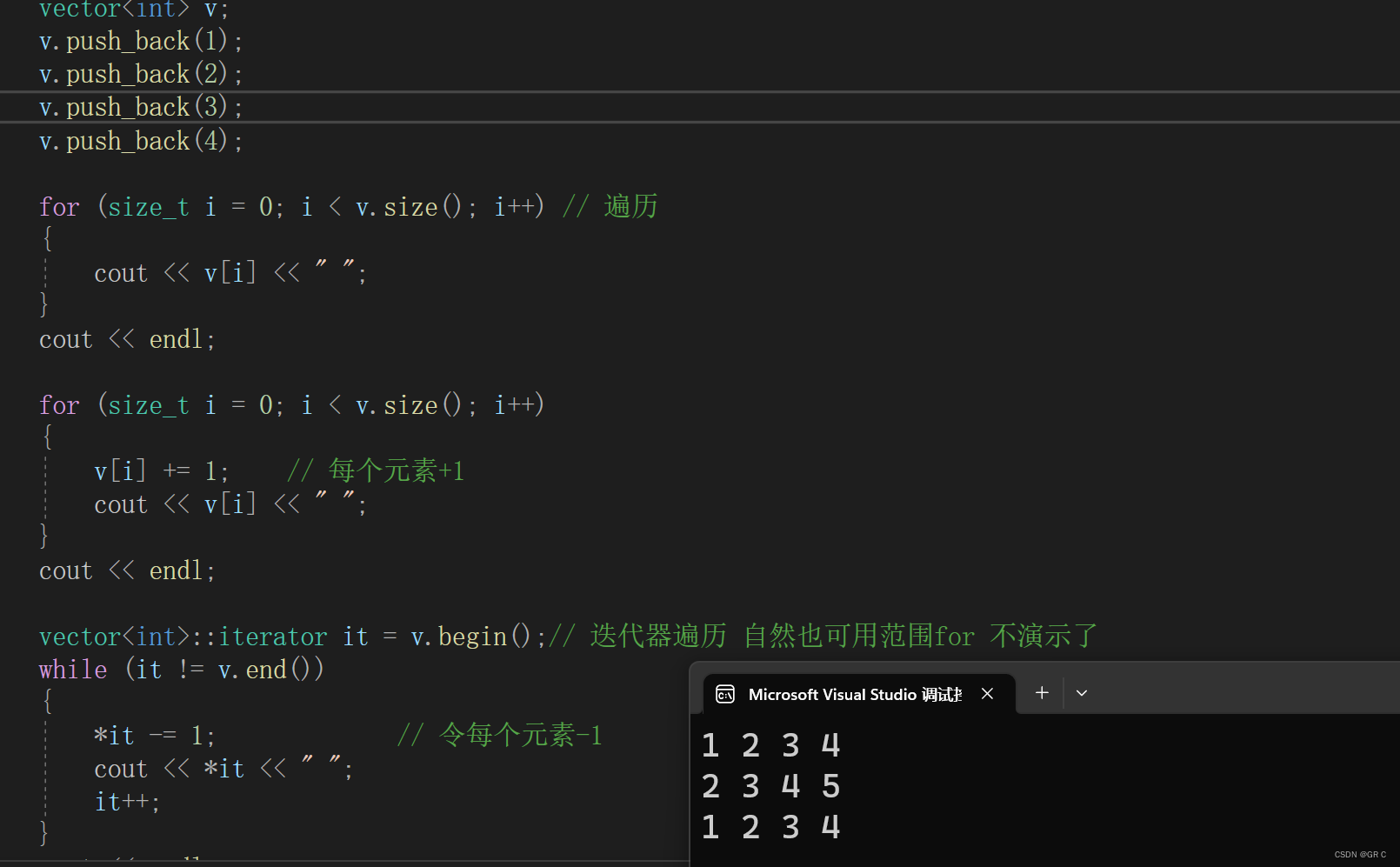
void Test1()
{
vector<int> v;
v.push_back(1);
v.push_back(2);
v.push_back(3);
v.push_back(4);
for (size_t i = 0; i < v.size(); i++) // 遍历
{
cout << v[i] << " ";
}
cout << endl;
for (size_t i = 0; i < v.size(); i++)
{
v[i] += 1; // 每个元素+1
cout << v[i] << " ";
}
cout << endl;
vector<int>::iterator it = v.begin();// 迭代器遍历 自然也可用范围for 不演示了
while (it != v.end())
{
*it -= 1; // 令每个元素-1
cout << *it << " ";
it++;
}
cout << endl;
}
int main()
{
Test1();
return 0;
}
1.4 vector 的容量和增删查改
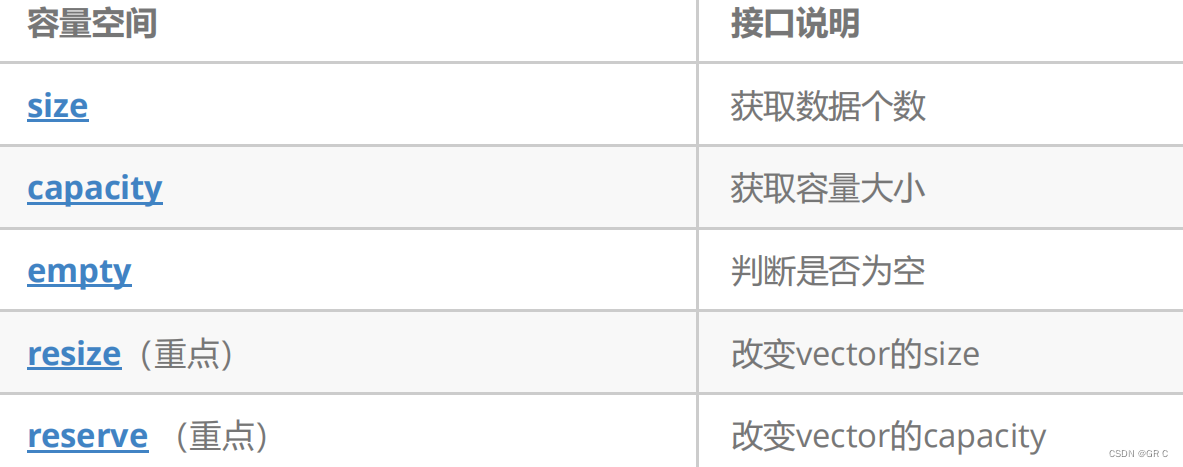
和string 一样， " reserve 和 resize 都是卖房子的（开空间的），reserve 只是把房子卖给你（开空间），而 resize 是一条龙服务，房子卖给你（开空间）之后还帮你搞装修（初始化），你还可以指定装修风格（初始化内容），如果不指定会按默认的简约风格装修（按类型的缺省值初始化）" resize 如果开的数据比之前更小，还会删除数据。
capacity 的代码在 VS 和 g++下分别运行会发现：VS下 capacity 是按 1.5 倍增长的，而 g++ 下 capacity 是按 2 倍增长的。 这个问题经常会考察，不要固化的认为，顺序表增容都是2倍，具体增长多少是根据具体的需求定义的。VS 是 PJ 版本 STL，g++ 是 SGI 版本 STL。
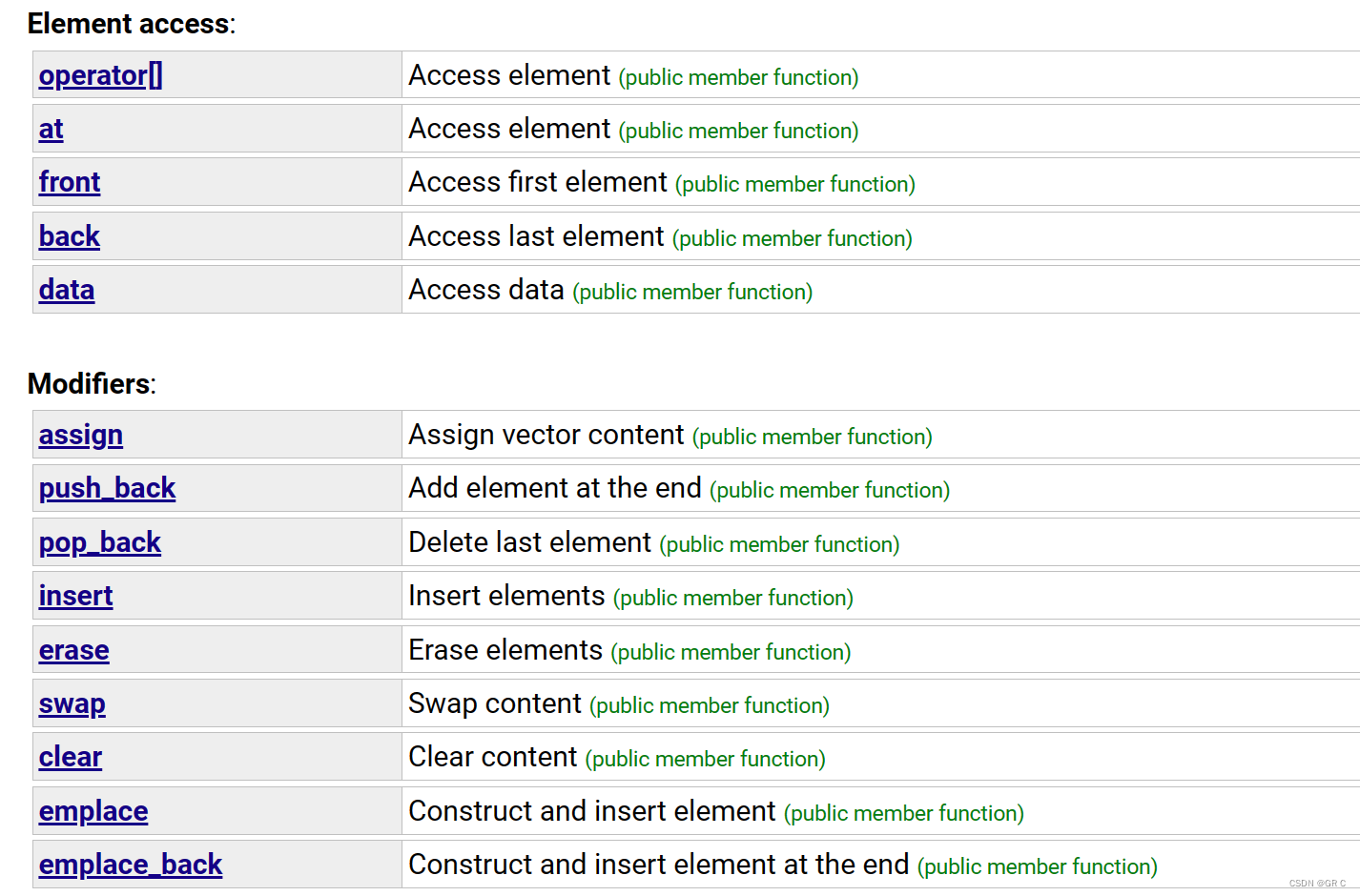
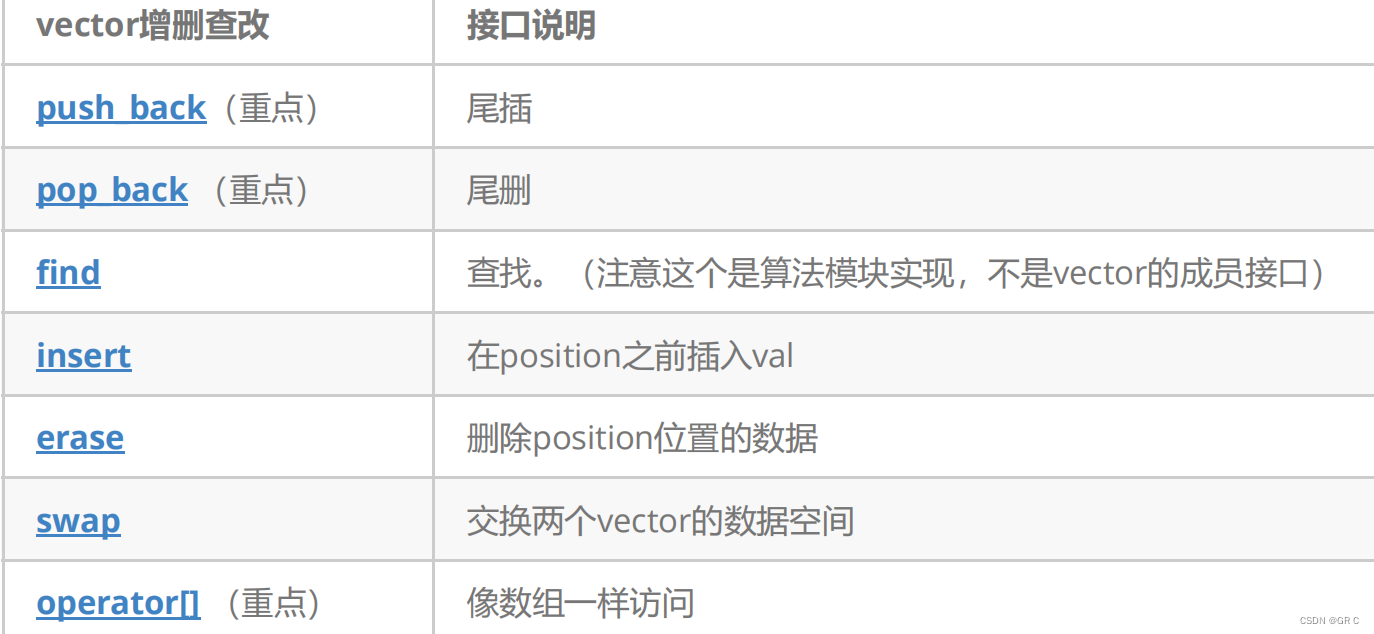
为什么 vector 不提供 find 接口：
string、map、set 都有 find() 用，凭什么 vector 和 list 没有？
其实，我们应该考虑的是 —— 为什么 string、map、set 能有 find 操作。
而 vector 之所以不提供 find ，是因为如果去查找元素效率就会是O（N）
但是"algorithm库" 里有通用的 find 操作
该 find 内部是从 begin 到 end 进行一次遍历，其复杂度是O（N）
值得一提的是，在C++中，凡是使用迭代器区间，都是左闭右开的
（map 和 set 接下来的章节会讲，以下部分可先作了解）
再去思考 map、set 为什么有 find() 通过迭代器从头到尾遍历 map 与 set 时，
得到的结果是按 key 排序的结果，而不是插入时的顺序，所以这两个容器没有 push_back 操作。
其实，插入到 map 与 set 中的元素会被组织到一颗红黑树上，红黑树是一颗平衡二叉树，
平衡二叉树是一颗二叉排序树，对一颗二叉排序树的查找有点像二分查找，复杂度是O（logN）
由于 map 与 set 的数据结构能有更快的查找方法，所以在容器内提供了 find 方法。
用的话大概就是这么用：这时候你就要记一下algorithm这个头文件怎么拼的了。
void Test2()
{
vector<int> v;
v.push_back(1);
v.push_back(2);
v.push_back(3);
v.push_back(4);
vector<int>::iterator ret = find(v.begin(), v.end(), 5);
// auto ret = find(v.begin(), v.end(), 3);
if (ret != v.end())
{
cout << "找到了" << endl;
}
else
{
cout << "没找到" << endl;
}
}很快哦，我们就玩完了vector，剩下的接口学过前面的应该都会了，下面我们写题了！
2. vector 相关选择题
1. 下面这个代码输出的是( )
#include <iostream>
#include <vector>
using namespace std;
int main(void)
{
vector<int>array;
array.push_back(100);
array.push_back(300);
array.push_back(300);
array.push_back(300);
array.push_back(300);
array.push_back(500);
vector<int>::iterator itor;
for(itor=array.begin();itor!=array.end();itor++)
{
if(* itor==300)
{
itor=array.erase(itor);
}
}
for(itor=array.begin();itor!=array.end();itor++)
{
cout<<*itor<<" ";
}
return 0;
}A.100 300 300 300 300 500
B.100 3OO 300 300 500
C.100 300 300 500
D.100 300 500
E.100 500
F.程序错误
2. std::vector::iterator 没有重载下面哪个运算符( )
A.==
B.++
C.*
D.>>
3. 下面有关vector和list的区别，描述错误的是( )
A.vector拥有一段连续的内存空间，因此支持随机存取，如果需要高效的随机存取,应该使用vector
B.list拥有一段不连续的内存空间，如果需要大量的插入和删除，应该使用list
C.vector<int>::iterator支持“+”、“+=”、“<”等操作符
D.list<int>::iterator则不支持“+”、“+=”、“<”等操作符运算，但是支持了[ ]运算符
4.下面程序的输出结果正确的是( )
int main()
{
int ar[] = {1,2,3,4,5,6,7,8,9,10};
int n = sizeof(ar) / sizeof(int);
vector<int> v(ar, ar+n);
cout<<v.size()<<":"<<v.capacity()<<endl;
v.reserve(100);
v.resize(20);
cout<<v.size()<<":"<<v.capacity()<<endl;
v.reserve(50);
v.resize(5);
cout<<v.size()<<":"<<v.capacity()<<endl;
}A.10:10 20:100 5:50
B.10:20 20:100 5:100
C.10:10 20:100 5:100
D.10 10 20:20 20:50
5. T是一个数据类型，关于std::vector::at 和 std::vector::operator[] 描述正确的是( )
A.at总是做边界检查， operator[] 不做边界检查.
B.at 不做边界检查， operator[] 做边界检查.
C.at和operator[] 都是会做边界检查的
D.以上都不对
3. vector 相关OJ题
（可以先刷一部分熟悉C++的刷题方式，后面再回来刷）
136. 只出现一次的数字 - 力扣（LeetCode）
难度简单
给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。
找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。
示例 1 ：
输入：nums = [2,2,1]
输出：1
示例 2 ：
输入：nums = [4,1,2,1,2]
输出：4
示例 3 ：
输入：nums = [1]
输出：1
提示：
-
1 <= nums.length <= 3 * 10^4 -
-3 * 104 <= nums[i] <= 3 * 10^4 -
除了某个元素只出现一次以外，其余每个元素均出现两次。
class Solution {
public:
int singleNumber(vector<int>& nums) {
}
};解析代码：
以前讲异或讲过的单身狗，直接重拳出击：
class Solution {
public:
int singleNumber(vector<int>& nums) {
int val = 0;
for(const auto& e : nums)
{
val ^= e;
}
return val;
}
};118. 杨辉三角 - 力扣（LeetCode）
难度简单
给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中，每个数是它左上方和右上方的数的和。
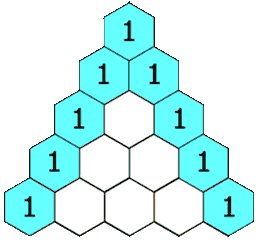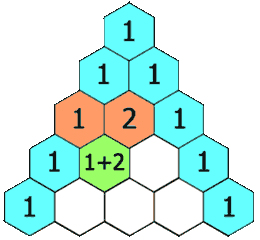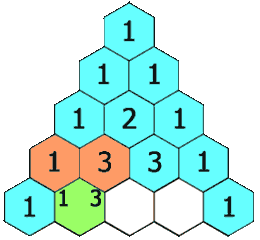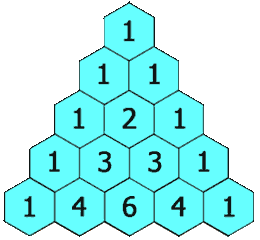
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
-
1 <= numRows <= 30
class Solution {
public:
vector<vector<int>> generate(int numRows) {
}
};解析代码：
杨辉三角写过类似的，这换成C++，vector 里面有个 vector<int> ，可以先理解为二维数组写：
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> vv;
vv.resize(numRows);
for (size_t i = 0;i < numRows;i++)// 开空间和把每一行的第一个和最后一个置为1
{
vv[i].resize(i + 1, 0);
//vv[i][0] = vv[i][vv[i].size() - 1] = 1;
vv[i].front() = vv[i].back() = 1;// 即上一行注释掉的代替
}
for (size_t i = 0;i < vv.size();i++)// 填充剩下的数据
{
for (size_t j = 0;j < vv[i].size();j++)
{
if (vv[i][j] == 0)
{
vv[i][j] = vv[i - 1][j - 1] + vv[i - 1][j];
}
}
}
return vv;
}
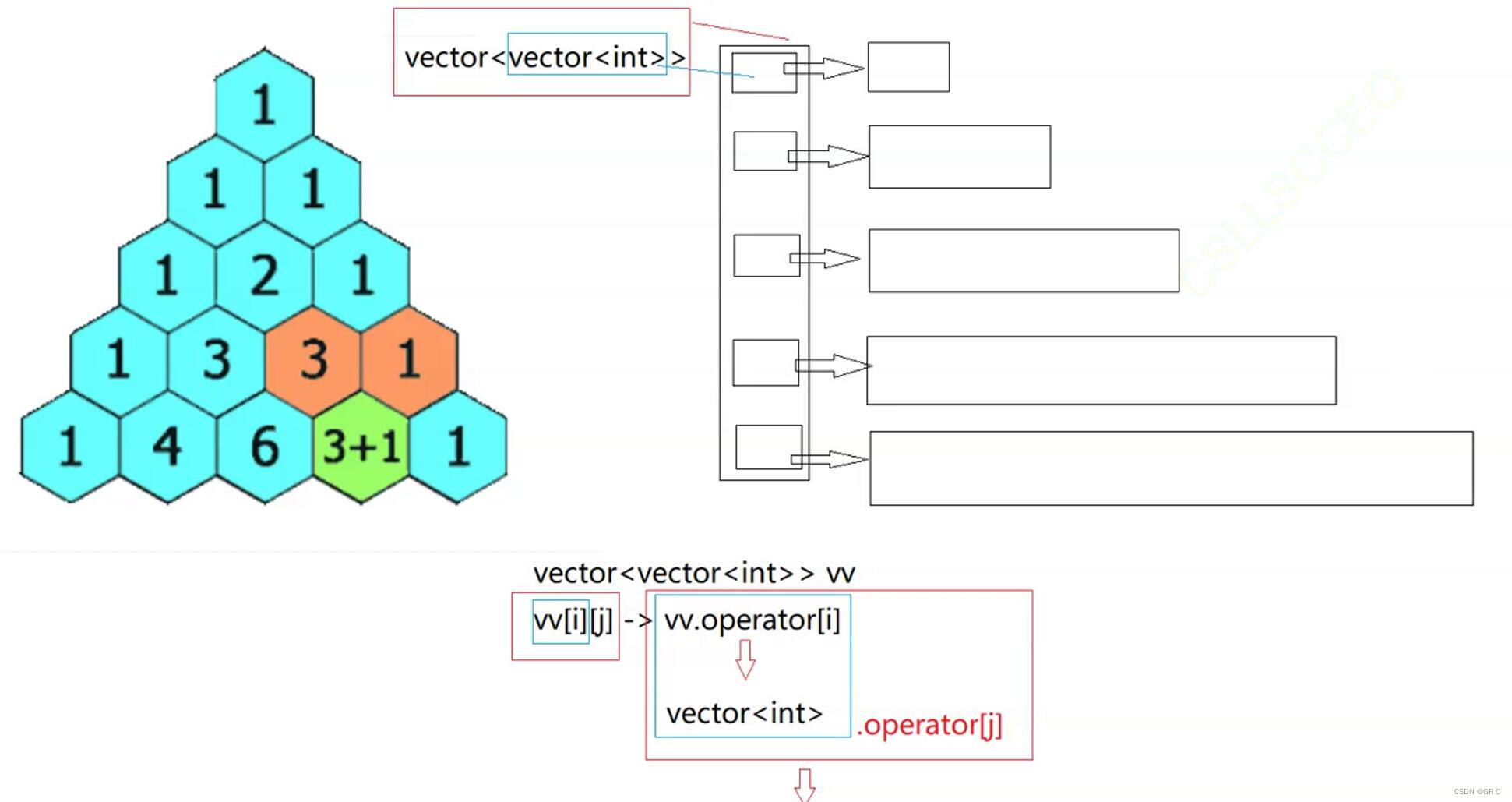
};这里的vector<vector<int>>空间上就是和二维数组类似的，操作就是调用了两次[ ] 运算符重载：
26. 删除有序数组中的重复项 - 力扣（LeetCode）
难度简单
给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：
- 更改数组
nums，使nums的前k个元素包含唯一元素，并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。 - 返回
k。
示例 1：
输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2：
输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示：
1 <= nums.length <= 3 * 10^4-104 <= nums[i] <= 10^4nums已按 升序 排列
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
}
};解析代码：
用C语言写过了，再次重拳出击，复制粘贴改一点点：
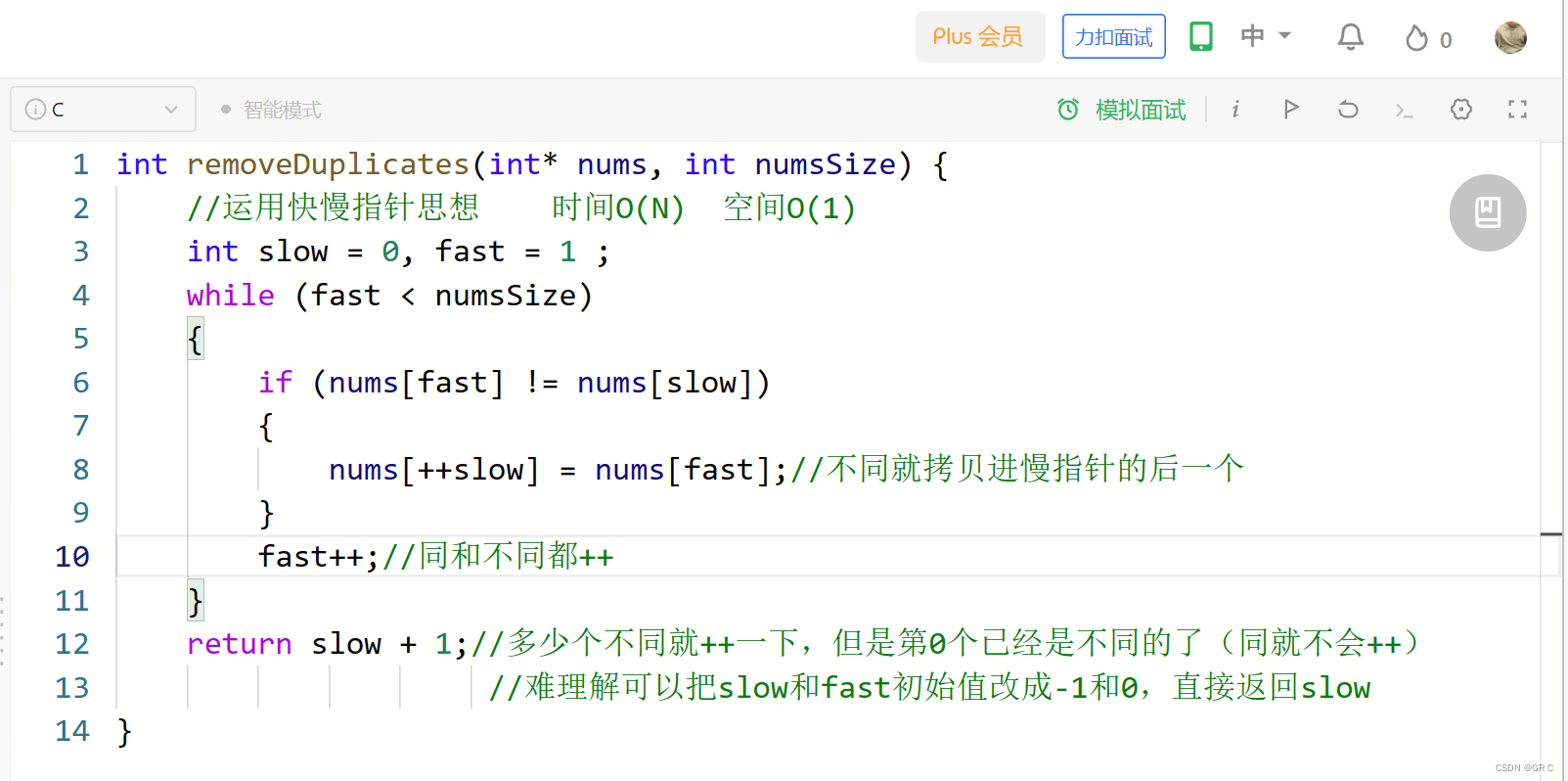
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
//运用快慢指针思想 时间O(N) 空间O(1)
int slow = 0, fast = 1;
while (fast < nums.size())
{
if (nums[fast] != nums[slow])
{
nums[++slow] = nums[fast];//不同就拷贝进慢指针的后一个
}
fast++;//同和不同都++
}
nums.resize(slow + 1);// 加不加都行，因为这题不用删除后面的元素，但其它题用呢？
return slow + 1;//多少个不同就++一下，但是第0个已经是不同的了（同就不会++）
//难理解可以把slow和fast初始值改成-1和0，直接返回slow
}
};137. 只出现一次的数字 II - 力扣（LeetCode）
难度中等
给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且不使用额外空间来解决此问题。
示例 1：
输入：nums = [2,2,3,2]
输出：3
示例 2：
输入：nums = [0,1,0,1,0,1,99]
输出：99
提示：
-
1 <= nums.length <= 3 * 10^4 -
-2^31 <= nums[i] <= 2^31 - 1 -
nums中，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次
class Solution {
public:
int singleNumber(vector<int>& nums) {
}
};解析代码1：
O（N^2）的笨蛋遍历：
class Solution {
public:
int singleNumber(vector<int>& nums) {
size_t i = 0;
for (; i < nums.size(); ++i)
{
int cnt = 0;
for (size_t j = 0; j < nums.size(); ++j)
{
if (nums[i] == nums[j])
{
cnt++;
}
if (cnt == 1 && j == nums.size() - 1)
{
return nums[i];
}
}
}
return nums[i];
}
};解析代码2:(sort排序)
这题还可以用排序的方法，我们以前学了八大排序，时间复杂度O（N*logN）的几大排序写起来都挺麻烦的，C++提供了这么库函数，怎么能少得了排序呢？有些人已经听过了algorithm里面的sort排序，sort的底层是快排加上了各种优化，时间复杂度也是O（N*logN），传个左闭右开的区间，它默认是排升序的，排降序会用到后面学的仿函数，后面再讲，排升序现在够了：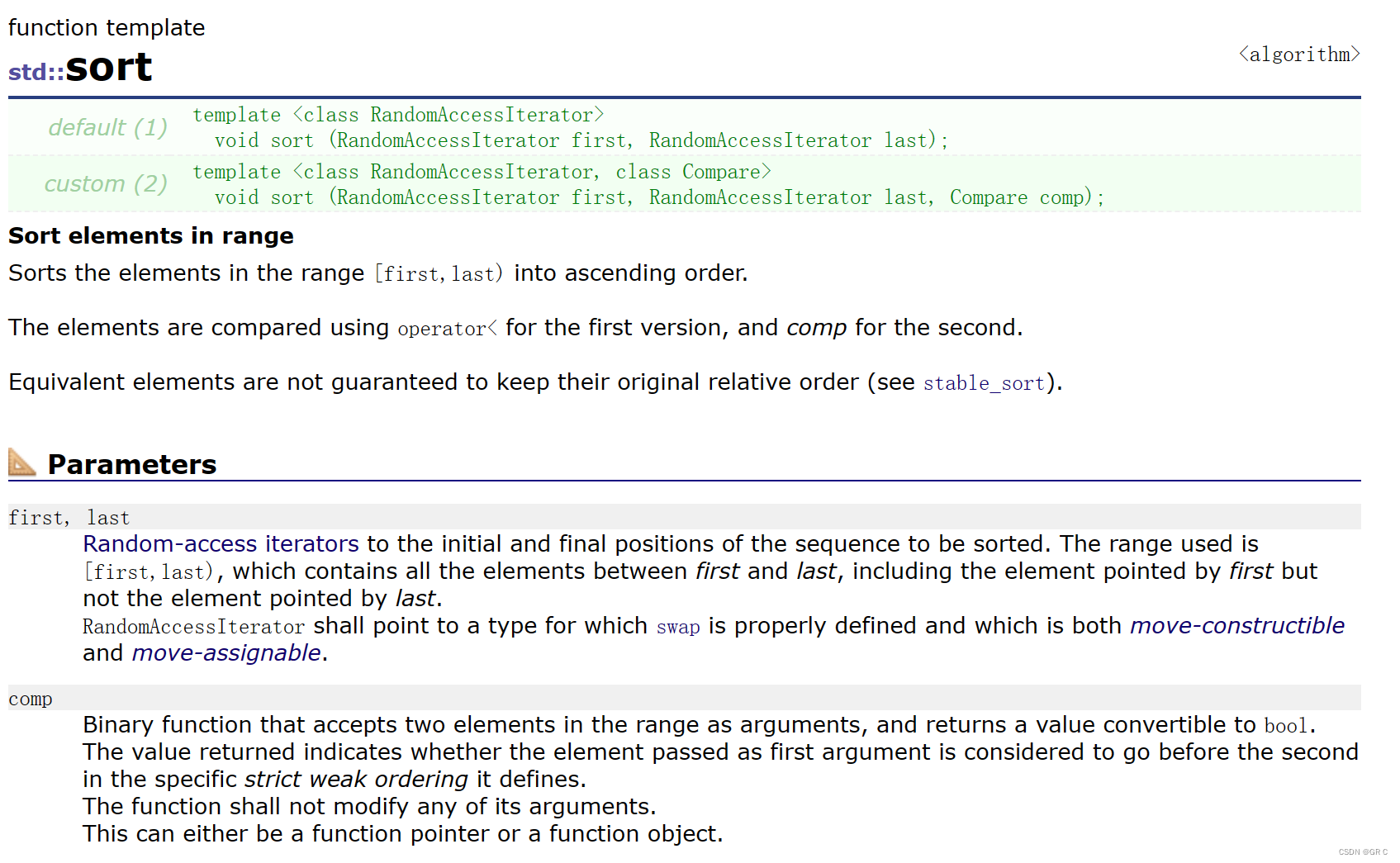
代码：
class Solution {
public:
int singleNumber(vector<int>& nums) {
sort(nums.begin(),nums.end());
int left = 0,right = 1;
while(right < nums.size())
{
if(nums[left] == nums[right])
{
right += 3;
left += 3;
}
else
{
return nums[left];
}
}
return nums[left];
}
};260. 只出现一次的数字 III - 力扣（LeetCode）
难度中等
给你一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1：
输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案。
示例 2：
输入：nums = [-1,0]
输出：[-1,0]
示例 3：
输入：nums = [0,1]
输出：[1,0]
提示：
-
2 <= nums.length <= 3 * 10^4 -
-2^31 <= nums[i] <= 2^31 - 1 -
除两个只出现一次的整数外，
nums中的其他数字都出现两次
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
}
};解析代码：
这也可以用排序，但这是以前写过的找两个单身狗的题：时间复杂度为O（N）
C语言进阶21收尾(编程作业)(atoi，strncpy,strncat,offsetof模拟实现+找单身狗+宏交换二进制奇偶位）_GR C的博客-CSDN博客
如果我们按照只出现一次的数字的思路直接异或 肯定只会出来一个四不像数
假设数组1 2 3 3 1 4
我们把 两个单身狗分成两个组
而组中其他的数字就都不是单身狗
此时我们在分组异或就分别得到了2个单身狗
问题 我们以什么为依据分组？
依据 二进制位 异或把相同的数字变成0，不同的数字变成1，
根据1在哪位 就说明单身狗这个的二进制位不同 ，按照这个二进制位分（这就是那个四不像的数）
两个单身狗是不可能进到一组的
① 我们依然把数组中所有数字异或到一起 然后判断这个数字的二进制位 比如有两个单身狗2和4
0010 和0100最后异或完毕得到的二进制位是 0110 说明两个单身狗数字的二进制最后位是相等
我们左移一(cnt)位得到了1 就说明 两个单身狗数字的倒数第二位二进制数 不相等
② 让数组中所有的数字左移一(cnt)位 如果等于 1 放进第一个数组中
如果等于0 放进第二个数组中
③ 把数组中的数字全部异或就得到了 2个单身狗
代码：
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
int sum = 0;
for (const auto& e : nums)
{
sum ^= e;
}
int cnt = 0;
for (int i = 0;i < 32;++i)
{
if (sum & (1 << i))// 第几位是1结果就是1
{
cnt = i;// 记录下来
}
}
vector<int> v = { 0,0 };// C++11的初始化,类似数组
for (const auto& e : nums)
{
if (e & (1 << cnt))
{
v[0] ^= e;
}
else
{
v[1] ^= e;
}
}
return v;
}
};剑指 Offer 39. 数组中出现次数超过一半的数字 - 力扣（LeetCode）
169. 多数元素 - 力扣（LeetCode）
数组中出现次数超过一半的数字_牛客题霸_牛客网 (nowcoder.com)
（上面三题都是一样的）
难度简单
数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。
你可以假设数组是非空的，并且给定的数组总是存在多数元素。
示例 1:
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2
限制：
1 <= 数组长度 <= 50000
进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
class Solution {
public:
int majorityElement(vector<int>& nums) {
}
};解析代码1:(sort)
上面三题用sort排序都能过，不过时间复杂度为 O(N*logN)：
class Solution {
public:
int majorityElement(vector<int>& nums) {
sort(nums.begin(),nums.end());
return nums[nums.size()/2];
}
};解析代码2:(摩尔投票法)
如果我们后面学了哈希表，后面比较容易想到的就是用哈希表，时间O(N)，空间O(N/2)
还是没有达到进阶，我们现在学另一种解法：摩尔投票法，时间O(N)，空间O(1)
可以理解成混战极限一换一，不同的两者一旦遇见就同归于尽，
最后活下来的值都是相同的，即要求的结果：
（这种方法一般人都想不到，理解就行，以后遇到就会了）
class Solution {
public:
int majorityElement(vector<int>& nums) {
int res = 0, count = 0;
//[1, 2, 3, 2, 2, 2, 5, 4, 2] //放个例子好理解
for(int i = 0; i < nums.size(); i++) // 遍历
{
if(count == 0)//count=0就更换候选人，投他一票
{
res = nums[i];
count++;
}
else // 开始记票
{
res == nums[i] ? count++ : count--;
}
}
return res;
}
};17. 电话号码的字母组合 - 力扣（LeetCode）
难度中等
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
示例 1：
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2：
输入：digits = ""
输出：[]
示例 3：
输入：digits = "2"
输出：["a","b","c"]
提示：
-
0 <= digits.length <= 4 -
digits[i]是范围['2', '9']的一个数字。
class Solution {
public:
vector<string> letterCombinations(string digits) {
}
};解析代码：
存储每个数字对应的所有可能的字母，然后进行回溯操作。（像前面树的递归一样）
回溯过程中维护一个字符串，表示已有的字母排列（如果未遍历完电话号码的所有数字，则已有的字母排列是不完整的）。该字符串初始为空。每次取电话号码的一位数字，从存储中获得该数字对应的所有可能的字母，并将其中的一个字母插入到已有的字母排列后面，然后继续处理电话号码的后一位数字，直到处理完电话号码中的所有数字，即得到一个完整的字母排列。然后进行回退操作，遍历其余的字母排列。
回溯算法用于寻找所有的可行解，如果发现一个解不可行，则会舍弃不可行的解。
在这道题中，由于每个数字对应的每个字母都可能进入字母组合，
因此不存在不可行的解，直接穷举所有的解即可。贴一个动画题解链接：
通俗易懂+动画演示 17. 电话号码的字母组合 - 电话号码的字母组合 - 力扣（LeetCode）
class Solution {
string arr[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
void _letterCombinations(const string& digits,size_t i,string& combinStr,vector<string>& strV)
{
if(i == digits.size())
{
strV.push_back(combinStr);
return;
}
string str = arr[digits[i]-'0'];
for(size_t j = 0 ; j < str.size() ; j++)
{
_letterCombinations(digits,i+1,combinStr+=str[j],strV);
combinStr.pop_back();
}
}
vector<string> letterCombinations(string digits) {
string combinStr;
vector<string> strV;
if(digits.empty())
{
return strV;
}
_letterCombinations(digits,0,combinStr,strV);
return strV;
}
};剑指 Offer 42. 连续子数组的最大和 - 力扣（LeetCode）
53. 最大子数组和 - 力扣（LeetCode）
连续子数组的最大和_牛客题霸_牛客网 (nowcoder.com)
（这三题也是一样的，这其实是一道非常简单的动态规划（dp））
难度简单
输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
提示：
-
1 <= arr.length <= 10^5 -
-100 <= arr[i] <= 100
class Solution {
public:
int maxSubArray(vector<int>& nums) {
}
};解析代码：
max函数是库里有的，直接得到两个数的较大值。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ret = nums[0];
for (int i = 1; i < nums.size(); i++)
{
nums[i] += max(nums[i - 1], 0);
ret = max(ret, nums[i]);
}
return ret;
}
};本篇完。
下一篇；模拟实现vector++迭代器失效问题
（虽然写OJ有点头疼，但是撑着头敲文章摘要时成就感拉满）
站长推荐
- stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述
【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述