【LeetCode】HOT 100（2）网站首页 技术交流

【LeetCode】HOT 100（2）

戊子仲秋 2024-07-04 18:01:02

简介【LeetCode】HOT 100（2）

题单介绍：

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。

题单介绍：

题目：5. 最长回文子串 - 力扣（Leetcode）

题目：11. 盛最多水的容器 - 力扣（Leetcode）

题目：5. 最长回文子串 - 力扣（Leetcode）

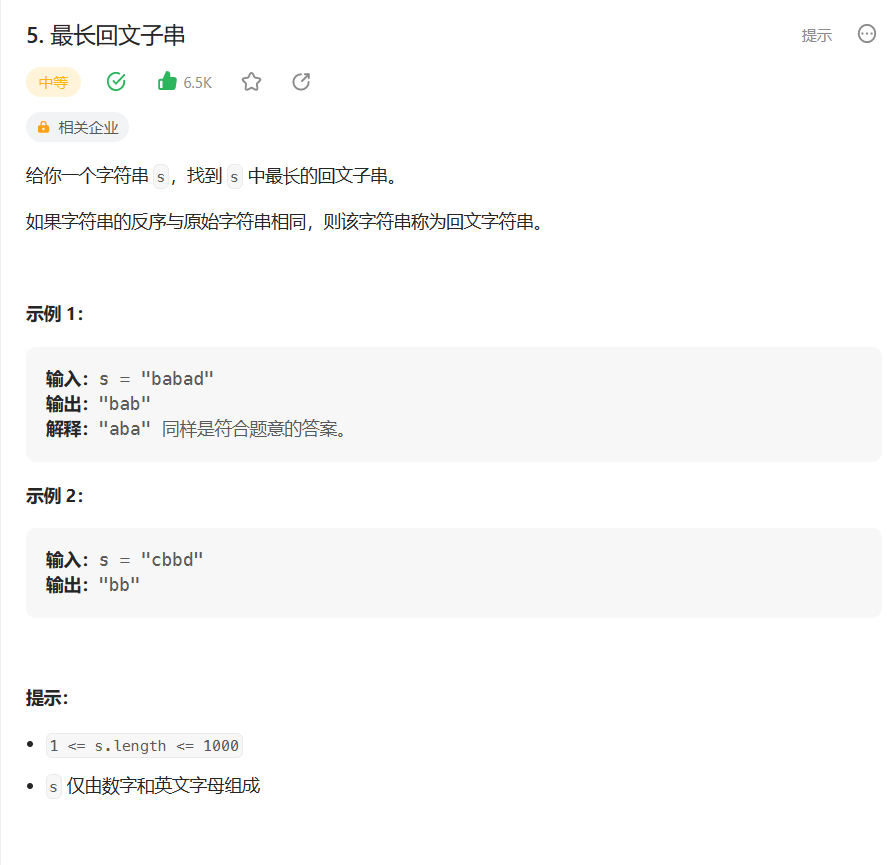
题目的接口：

class Solution {
public:
    string longestPalindrome(string s) {

    }
};

解题思路：

这道题我看很多题解都是用动态规划，

我动态规划不好，所以，我这道题用的是中心扩散的思路做的，

所以我就讲一讲中心扩散的思路：

直接遍历数组，

以遍历的时候的每个下标为中心，向两边扩散，

计算出这个回文串的大小，如果当前的回文串最长，

就更新他的：起始边界start，结束边界end，长度max_len。

最后将最长的回文串用substr截出来返回即可。

代码如下：

代码：

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.size();
        if(len <= 1) return s; //特殊情况直接返回
        int start = 0;
        int end = 0;
        int max_len = 0;
        for(int i = 0; i < len; i++) { //遍历字符串
            int len1 = exp_center(s, i, i); //aba情况
            int len2 = exp_center(s, i, i + 1); //abba情况
            max_len = max(max(len1, len2), max_len); //更新最大值
            if(max_len > end - start + 1) { //如果这次是最大值，更新边界
                start = i - ((max_len - 1) / 2); //考虑abba情况的下标，所以要-1
                end = i + (max_len / 2); 
            }
        }
        return s.substr(start, max_len); 
    }
private: //计算当前回文串的大小
    int exp_center(const string& s, int l, int r) {
        while(l >= 0 && r < s.size() && s[l] == s[r]) {
            l--;
            r++;
        }
        return r - l - 1;
    }
};

过过过过啦！！！！

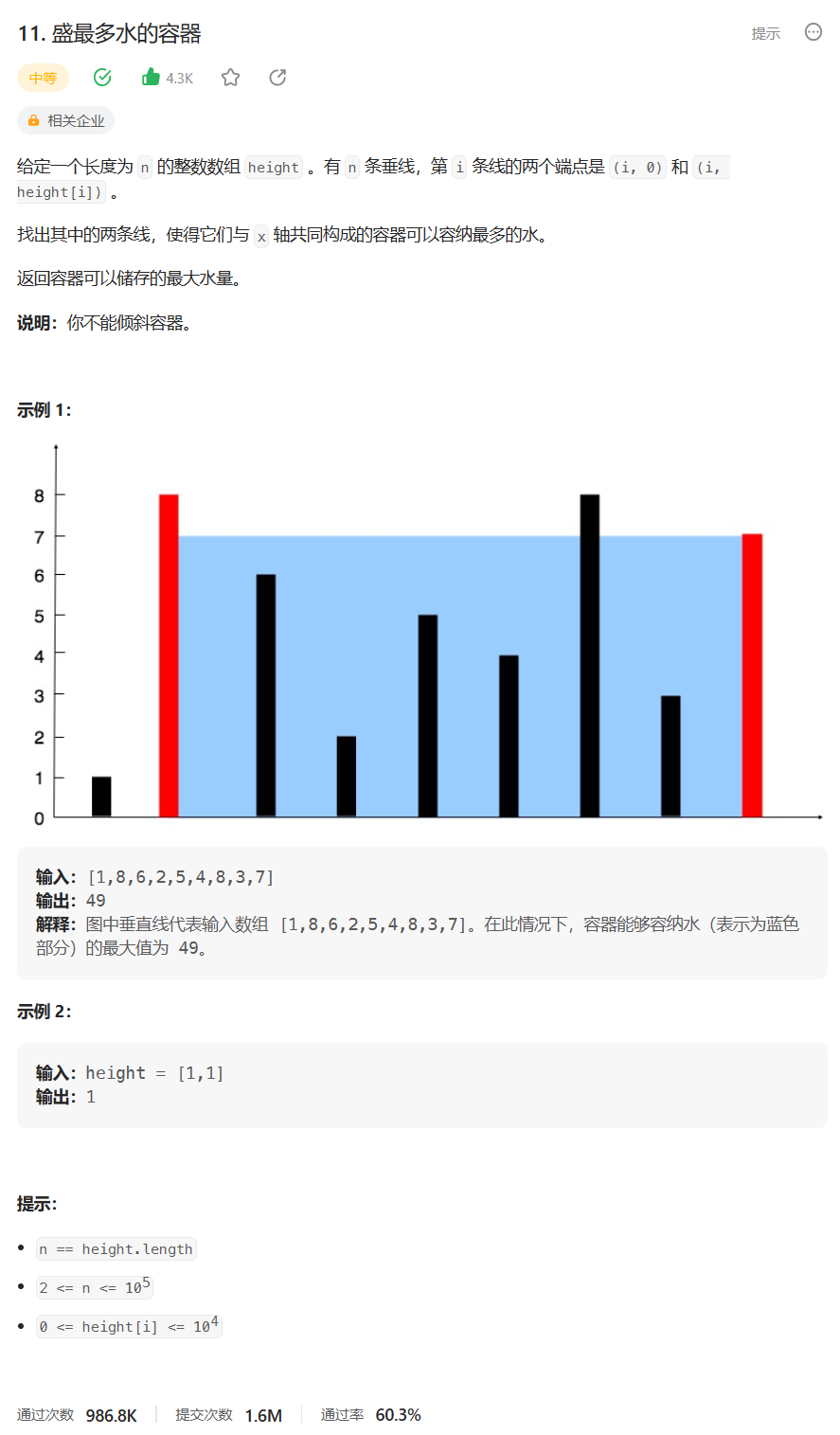
题目：11. 盛最多水的容器 - 力扣（Leetcode）

题目的接口：

class Solution {
public:
    int maxArea(vector<int>& height) {

    }
};

解题思路：

这道题的解题思路很巧妙，我一开始也是想不出来，

具体是这样子的：

我们通过双指针来解决，

一个指针在最左，一个指针在最右：

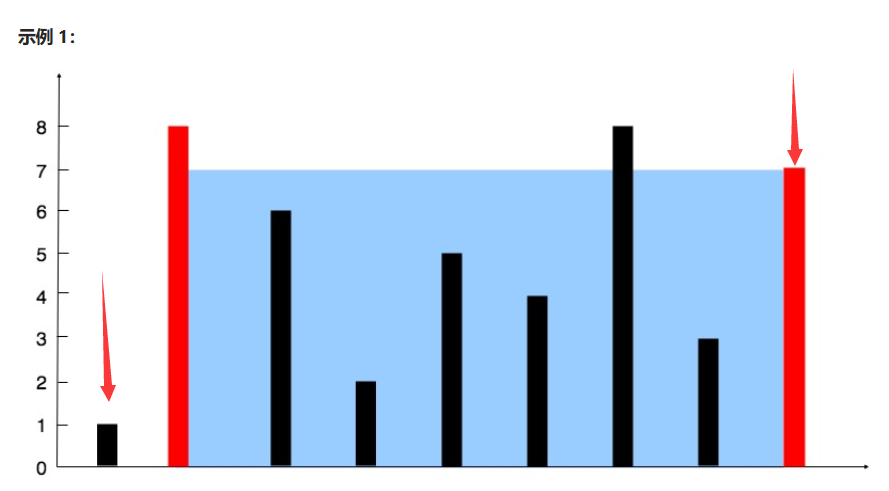
然后，比较两个指针指向的值的大小，

更新小的那边的指针：

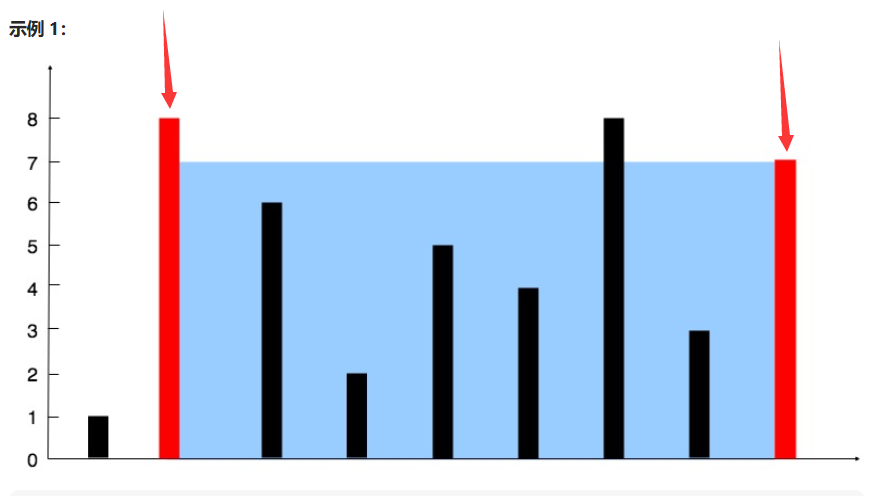然后每次更新最大的面积即可，

这个原理用通俗点的话来讲就是：

每次更新指针范围，盛水的容器长度肯定会变小，想让盛水量更多，找最大值，

只有让更矮的线更新，继续找更高的线才有可能让盛水量更多。

代码逻辑比较简单，我就不加注释了。

代码如下：

代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1;
        int max_val = 0;
        while(left != right) {
            max_val = max(max_val, min(height[left], height[right]) * (right - left));
            if(height[left] < height[right]) {
                left++;
            }
            else right--;
        }
        return max_val;
    }
};