动态规划专题一(动态规划的基本模型)网站首页 学无止境

动态规划专题一(动态规划的基本模型)

书鸢1236 2024-07-04 11:18:03

简介动态规划专题一(动态规划的基本模型)

先上例题1

1258：【例9.2】数字金字塔

信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)

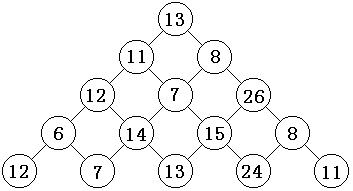
1258：【例9.2】数字金字塔

时间限制: 1000 ms 内存限制: 65536 KB
提交数: 36341 通过数: 21547

【题目描述】

观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。

在上面的样例中,从1313到88到2626到1515到2424的路径产生了最大的和8686。

【输入】

第一个行包含R(1≤R≤1000)�(1≤�≤1000)，表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

所有的被供应的整数是非负的且不大于100100。

【输出】

单独的一行，包含那个可能得到的最大的和。

【输入样例】

5
13
11 8
12 7  26
6  14 15 8
12 7  13 24 11

【输出样例】

题目要求从顶点出发到尾端找到一条路径使得改路径权重和最大

一:暴搜

显然对于这个数字金字塔我们可以直接使用暴搜遍历所有的路径可能,通过比较得到最大值

这时对于不同的输入n,我们每一次搜的次数将爆炸形增长。

分析其中原因:对于同一个点会经过多次计算,而每一次选择都有俩个,我们以答案视角出发,对于图中n个点,它的最优路径都是唯一固定的,也就是我们在枚举路径时,其实有很多次搜索都是无效的,因为只要我们找到一次了改点的最优路径,后面的搜索都是无用功。

二:记忆化搜索

分析完一

在一的基础优化,设置一个数组用于存放n号结点最优路径的权重,一旦数组中记录了其最优解就不再进行搜索.这就是记忆化搜索

三:动态规划

再分析一下二,其实也会有一些无用功,例如既然已经知道了改路径最优解,但每一次搜索还是会搜索到这个点,只不过改点往下不再搜索了。并且搜索完之后我们也要最各项结果遍历得到最大项

有没有更简单快捷的方式?

换一个思路 ==> 从下往上搜索

简单思考一下,对于上层结点路径的最优解取决于其下层结点的权重

对于每一层结点只有俩个选择,其中最后一层没有选择,那我们不妨从n - 1层开始对每一个结点的选择进行枚举,每一次都选择最大项,层层向上传递答案,此时我们数组的含义就是经过MAP[i][j]结点路径最优解的权重,最后我们的MAP[0][0]就是整个数字金字塔从最上层到底层最优解的权重。

这就是动态规划的基础思想,根据已有规则,推出一个方法(或者是DP公式)帮助我们找到问题的答案

#include<bits/stdc++.h>
#define endl '
'
using namespace std;
int n, m;
void slove()
{
    cin >> n;
    vector<vector<int>>MAP(n);
    for(int i = 0;i < n; i++)
        for(int j = 0;j < i + 1;j++)
        {
            cin >> m;
            MAP[i].emplace_back(m);
        }
    //核心代码
    for(int i = n - 2;i >= 0;i--)
        for(int j = 0; j < MAP[i].size();j++)
            MAP[i][j] += max(MAP[i + 1][j],MAP[i + 1][j + 1]);
    cout << MAP[0][0] << endl;
}
int main()
{
    cin.tie(0) -> sync_with_stdio(false);
        slove();
    return 0;
}

这里的DP公式就是 MAP[i][j] += max(MAP[i + 1][j],MAP[i + 1][j + 1]);

1259：【例9.3】求最长不下降序列

【题目描述】

例如13，7，9，16，38，24，37，18，44，19，21，22，63，15。例中13，16，18，19，21，22，63就是一个长度为77的不下降序列，同时也有7 ，9，16，18，19，21，22，63组成的长度为88的不下降序列。

【输入样例】

14
13 7 9 16 38 24 37 18 44 19 21 22 63 15

【输出样例】

max=8
7 9 16 18 19 21 22 63

这题如果是连续的子序列很明显一个简单的滑动窗口就可以轻松解决了,那么面对这种情况又该怎么办呢?

定义DP数组状态:对于任意DP[i]表示以i号元素作为结尾的不下降序列大小

首先还是先分析子序列的关系

对任意 1 <= i < j <= n

若满足num[j] >= num[i] == >> 说明以num[j]结尾的子序列长度是在num[i] 的基础上新填num[j]元素不难理解例: 1 2 3 ==>> 以1结尾的子序列长度为1 , 2满足>= 1的条件,将2纳入序列中间,此时以2结尾的最长子序列为2

对于DP数组转移表达式为DP[j] = DP[i] + 1;

尤其要注意的是实际数据的元素并非有序的,因此对于同一个数在不同位置能得到的子序列长度也是不同的,并且元素排序也是杂乱无章的,因此对于所有满足num[j] >= num[i]的条件不能简单的直接转移而是在所有元素中选择最优解 == >> 即 DP[j] = max(DP[j]，DP[i] + 1);

#include<bits/stdc++.h>
#define endl '
'
using namespace std;
int n, m, ans;
void mycout(vector<int> pre,vector<int> num,int x)
{
    if(!pre[x]){cout<<num[x];return;}
    mycout(pre,num,pre[x]);
    cout << " " << num[x];
}
void slove()
{
    cin >> n;
    vector<int>num(n + 1),DP(n + 1,1),pre(n + 1,0);
    for(int i = 1;i <= n;i++)
        cin >> num[i];
    for(int i = 1;i <= n;i++)
    {//枚举n个结尾
        for(int j = 1; j < i;j++)
        {
            if(num[i] >= num[j] && DP[i] < DP[j] + 1)
            {//保证不下降的前提,为了确保前端数组的准确性将DP[i] = max(DP[i],DP[j] + 1)取最大的条件放到if语句进行维护
                DP[i] = DP[j] + 1;
                pre[i] = j;
            }
            ans < DP[i] ? ans = DP[i], m = i : ans = ans;
        }
    }
    cout << "max=" << ans << endl;
    mycout(pre,num,m);
}
int main()
{
    cin.tie(0) -> sync_with_stdio(false);
        slove();
    return 0;
}

1260：【例9.4】拦截导弹(Noip1999)

O(N ^ 2)做法 + 优化

#include<bits/stdc++.h>
#define endl '
'
using namespace std;
const int maxn = 1010;
int n, m, ans,res;
void slove()
{
    vector<int>num;
    while(cin >> m)num.emplace_back(m);
    vector<int>DP(num.size() + 1,1),is(num.size(),0);
    for(int i = 0;i < num.size();i++)
    {//枚举n个结尾
        for(int j = 0; j < i;j++)
        {
            if(num[i] <= num[j])
            DP[i] = max(DP[i],DP[j] + 1);
        }
       ans = max(ans,DP[i]);
    }
    int ok = 0;//已拦截导弹数
    int head = 0;//第1个未被拦截的导弹编号
    while(ok < num.size())
    {
        int i = head;
        int H = INT_MAX;//当前可拦截的最大高度
        for(int j = head; j < num.size();j++)
        {
            if(num[j] <= H && is[j] == 0)
            {
                is[j] = true;
                H = num[j];
                ok++;
            }
            else if(head == i && is[j] == 0)head = j;
        }
        res++;
    }
    cout << ans << endl << res;
}

int main()
{
    cin.tie(0) -> sync_with_stdio(false);
        slove();
    return 0;
}

O(nlogn)解法( 非动态规划)

#include<bits/stdc++.h>
#define endl '
'
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using namespace std;
int n,m,k,A,B,N,M,K,res,ok;
const int maxn = 1e6 + 10;
bool cmp(int a,int b)
{
    return a >= b;
}
void sove()
{
    vector<int> num,D;
    while(cin >> m)num.emplace_back(m);
    D.emplace_back(num[0]);
    for(int i = 1;i < num.size();i++)
    {
        if(num[i] <= D.back())
           D.emplace_back(num[i]);
        else 
        {
            int T = lower_bound(D.begin() ,D.end() ,num[i] , cmp) - D.begin();
            D[T] = num[i];
        }
    }
    
    vector<bool>is(num.size());
    int head = 0;
    while(ok < num.size())
    {
        int i = head;
        int H = INT_MAX;//当前可拦截的最大高度
        for(int j = head; j < num.size();j++)
        {
            if(num[j] <= H && is[j] == 0)
            {
                is[j] = true;
                H = num[j];
                ok++;
            }
            else if(head == i && is[j] == 0)head = j;
        }
        res++;
    }
    cout << D.size() << endl << res;
}

int main()
{
    cin.tie(0) -> sync_with_stdio(false);
    sove();
    return 0;
}

O(nlogn)解法( 非动态规划)优化

#include<bits/stdc++.h>
#define endl '
'
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using namespace std;
int n, m, k, A, B, N, M, K, res, ok;
const int maxn = 1e6 + 10;
bool cmp(int a, int b)
{
    return a >= b;
}
void sove()
{
    vector<int> num, D;
    while (cin >> m)num.emplace_back(m);
    D.emplace_back(num[0]);
    for (int i = 1; i < num.size(); i++)
    {
        if (num[i] <= D.back())
            D.emplace_back(num[i]);
        else
        {
            int T = lower_bound(D.begin(), D.end(), num[i], cmp) - D.begin();
            D[T] = num[i];
        }
    }
    cout << D.size() << endl;
    D.clear();
    D.emplace_back(num[0]);
    for (int i = 1; i < num.size(); i++)
    {
        if (num[i] > D.back())
            D.emplace_back(num[i]);
        else
        {
            int T = lower_bound(D.begin(), D.end(), num[i]) - D.begin();
            D[T] = num[i];
        }
    }
    cout << D.size() << endl;
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    sove();
    return 0;
}