High-frequency Component Helps Explain the Generalization of Convolutional Neural Networks

公众号：EDPJ

目录

0. 摘要

1. 简介

2. 相关工作

3. 高频成分 & CNN 的泛化

3.1 CNN 利用高频成分

3.2 鲁棒性和准确性之间的权衡 

4. 在重新思考泛化之前重新思考数据

4.1 假设 

4.2 实验

4.3 遗留问题 

5. 训练启发式（Heuristics）

5.1 不同启发式的比较

5.2 关于批量归一化的假设

6. 对抗性攻防

6.1 内核平滑度与图像频率

6.2 稳健的模型具有光滑的内核

6.3 平滑内核提高了对抗鲁棒性 

7. Beyond 图像分类

7.1 LFC 性能下降

7.2 LFC 的性能提升 

8. 讨论：HFC 只是噪音吗？ 

9. 结论与展望

参考

S. 总结

S.1 核心思想

S.2 研究方法

S.3 分析

S.4 启发式

S.5 稳健性与卷积核平滑度

---

0. 摘要

我们研究了图像数据的频谱与卷积神经网络 (CNN) 的泛化行为之间的关系。 我们首先注意到 CNN 捕捉图像高频成分的能力。 这些高频成分几乎是人类无法察觉的。 因此，观察结果导致了与 CNN 的泛化行为相关的多个假设，包括对对抗性示例的潜在解释，对 CNN 在鲁棒性和准确性之间权衡的讨论，以及理解训练启发式的一些证据 。

1. 简介

深度学习在各种任务的预测建模方面取得了许多最新进展，但人们仍然对神经网络不直观的泛化行为感到震惊，例如记忆标签混洗（label-shuffled）数据的能力和对对抗性示例的脆弱性。

为了解释神经网络的泛化行为，已经逐步取得了许多理论突破，包括研究随机梯度下降的性质、不同的复杂性度量、泛化差距，以及来自不同模型或算法的更多视角。

在本文中，受先前关于卷积神经网络 (CNN) 可以从混杂信号和表面信号中学习的理解的启发，我们从数据的角度研究了 CNN 的泛化行为。和 [27] 一样，我们认为 CNN 的非直觉泛化行为是人类与模型之间感知差异的直接结果（如图 1 所示）：CNN 可以比人类以更高的粒度查看数据。

然而，与 [27] 不同的是，我们提供了对模型感知的这种高粒度的解释：CNN 可以利用人类无法感知的高频图像成分。

例如，图 2 显示了来自 CIFAR10 数据集的八个测试样本的预测结果，以及对应的高频和低频分量的预测结果。 对于这些例子，预测结果几乎完全由图像的高频成分决定，人类几乎无法感知。 另一方面，对于人类来说，低频分量看起来几乎与原始图像相同，但被模型预测为明显不同的东西。 

受上述经验观察的启发，我们进一步研究了 CNN 的泛化行为，并试图通过对输入图像频谱的差异响应来解释此类行为（Remark 1）。 我们的主要贡献总结如下：

• 我们通过提供 CNN 如何利用图像的高频分量来用准确性交换鲁棒性（推论 1）的示例，揭示了 CNN 的准确性和鲁棒性之间的现有权衡。 
• 以图像频谱为工具，我们提供假设来解释 CNN 的几种泛化行为，尤其是记忆标签混洗数据的能力。
• 我们提出的防御方法可以帮助提高 CNN 对简单攻击的对抗鲁棒性，而无需训练或微调模型。

2. 相关工作

深度学习的巨大成功吸引了大量致力于解释 CNN 泛化之谜的理论工作。

• 自从 Zhang 等人证明了几个成功的神经网络架构的有效容量足以记住随机标签，人们看到了关于这个明显的“悖论”的许多讨论的繁荣。
• Arpit 等人证明有效容量不太可能解释基于梯度方法训练的深度网络的泛化性能，因为训练数据在很大程度上决定了记忆。
• Kruger 等人通过在深度网络中训练随机标签时显示最大的 Hessian 特征值增加来进行实证论证。

对抗性示例的概念已成为与神经网络行为相关的另一个有趣的方向。 沿着这条线，研究人员发明了强大的方法，例如 FGSM、PGD 和许多其他方法来欺骗模型，这被称为攻击方法。 为了保护模型免受欺骗，另一组研究人员提出了多种方法（称为防御方法）。 这些只是提议的攻击和防御方法的悠久历史中的一些亮点。 可以参考综合评论进行详细讨论。

然而，在提高鲁棒性的同时，这些方法可能会出现预测精度的轻微下降，这导致了鲁棒性和准确性之间权衡的另一个讨论话题。一些实证结果表明，在生成的对抗性示例上，精准的模型往往更稳健。 另外的工作则认为，虽然增加的鲁棒性主要是由于准确性的提高，但更精准的模型（例如 VGG、ResNet）实际上不如 AlexNet 稳健。

3. 高频成分 & CNN 的泛化

我们首先设置本文中使用的基本符号：<x,y> 表示数据样本（图像和相应的标签）。f(·;θ) 表示一个卷积神经网络，其参数记为 θ。 我们使用 H 来表示人类模型，因此，f(·;H) 表示人类将如何对数据 进行分类。 l(·,·) 表示通用损失函数（例如，交叉熵损失）。 α(·,·) 表示评估预测准确性的函数（对于每个样本，如果样本被正确分类，则此函数产生 1.0，否则为 0.0）。 d(·,·) 表示评估两个向量之间距离的函数。 F(·)表示傅立叶变换； 因此，F^(−1) (·) 表示逆傅里叶变换。 我们使用 z 来表示样本的频率分量。 因此，我们有 z = F(x) 和 x = F^(−1) (z)。

请注意，傅里叶变换或其逆变换可能会引入复数。在本文中，我们简单地丢弃了 F^(−1) (·) 结果的虚部，以确保生成的图像可以像往常一样输入 CNN。

3.1 CNN 利用高频成分

我们分解原始数据 x = {x_l, x_h}，其中 x_l 和 x_h 表示 x 的低频分量（简称为 LFC）和高频分量（简称为 HFC）。 我们有以下四个等式：

其中 t(·; r) 表示根据超参数半径 r 将低频和高频分量与 z 分开的阈值函数。

为了正式定义 t(·; r)，我们首先考虑大小为 n × n 的灰度（单通道）图像，具有 N 个可能的像素值（换句话说，x ∈ N^(n×n)），然后我们有 z ∈ C^(n×n)，其中 C 表示复数。 我们使用 z(i, j) 来索引 z 在位置 (i, j) 的值，我们使用 c_i, c_j 表示质心 (centroid)。 我们将方程 z_l, z_h = t(z; r) 正式定义为： 

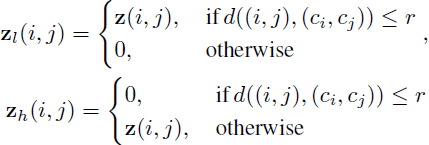
本文将 t(·;r) 中的 d(·,·) 视为欧式距离。 如果 x 有多个通道，则该过程独立地对像素的每个通道进行操作。 

Remark 1。假设（假设 1，A1）“只有 x_l 是人类可感知的，但 x_l 和 x_h 都是 CNN 可感知的”，我们有：

但是当 CNN 使用下式训练时

等价于

CNN 可能会学习利用 x_h 来最小化损失。 因此，CNN 的泛化行为对人类来说是不直观的。

请注意，“CNN 可能学会利用 x_h ” 与 “CNN 过拟合” 不同，因为 x_h 可以包含比特定于样本的特质更多的信息，并且这些更多信息可以在训练、验证和测试集中泛化，只是人类无法察觉。

由于假设 A1 已被证明在某些情况下成立（例如，在图 2 中），我们认为 Remark 1 可以作为对 CNN 泛化行为的解释之一。 例如，对抗样本可以通过扰动 x_h 生成； CNN 在标签混洗数据上将训练误差减少到零的能力可以看作是利用 x_h 和过度拟合样本特定特质的结果。 我们将在以下部分讨论更多内容。 

3.2 鲁棒性和准确性之间的权衡 

我们继续 Remark 1，从图像频率的角度讨论 CNN 在给定 θ 的鲁棒性和准确性之间的权衡。我们首先将 θ 的准确度正式表述为：

θ 的对抗鲁棒性表示为

其中 ε 是允许扰动的上限。

另一个假设（简称 A2）：对于模型 θ，存在一个样本 <x,y> 使得：

我们可以将我们的主要论点（Remark 1）扩展为正式陈述： 

推论 1。在假设 A1 和 A2 的情况下，存在样本 <x,y>，对于任何距离度量 d(·,·) 和边界 ε，只要 ε ≥ d(x, x_l)，模型 θ 无法准确（通过等式 1 评估为 1.0）且鲁棒地（通过等式 2 评估为 1.0）进行预测。

证明是前面讨论的直接结果，因此省略。 假设 A2 也可以通过经验验证（例如，在图 2 中），因此我们可以安全地声明推论 1 可以作为 CNN 的鲁棒性和准确性之间权衡的解释之一。

4. 在重新思考泛化之前重新思考数据

4.1 假设 

我们的第一个目标是对观察到的经验结果（神经网络可以轻松地拟合标签打乱的数据）提供一些直观的解释。 虽然我们毫不怀疑神经网络能够因其容量而记忆数据，但有趣的问题出现了：“如果神经网络可以轻松记忆数据，为什么它关心从数据中学习可泛化的模式，而不是直接记住一切以减少训练损失？”

在 Remark 1 中介绍的观点内，我们的假设如下：尽管与训练损失最小化的结果相同，但模型在两种情况下考虑了不同级别的特征：

• 在原始标签情况下，模型会先关注低频分量（LFC），然后逐渐关注高频分量（HFC），以达到更高的训练准确率。
• 在标签打乱的情况下，由于打乱导致 LFC 和标签之间的关联被删除，因此当 LFC 和 HFC 被同等对待时，模型必须记住图像。

4.2 实验

我们设置实验来检验我们的假设。 我们使用 CIFAR10 数据集的 ResNet-18 作为基础实验。 我们将在本文的其余部分使用的普通设置是使用 Adam 优化器运行 100 个 epoches 的实验，学习率设置为 10^(−4)，批量大小设置为 100，权重使用 Xavier 初始化进行初始化。像素都被归一化为 [0, 1]。 所有这些实验都在 MNIST、FashionMNIST 和 ImageNet 的一个子集中重复进行。 附录中报告了这些努力。 我们训练了两个模型，分别使用自然标签设置和打乱标签设置，分别表示为 M_natural 和 M_shuffle； M_shuffle 需要 300 个 epoches 才能达到相当的训练精度。 为了测试模型提取的信息的哪一部分，对于训练集中的任何 x，我们生成低频分量 x_l，其中 r 分别设置为 4、8、12、16。 我们测试了训练过程中这些低频数据集合的训练准确性如何变化。

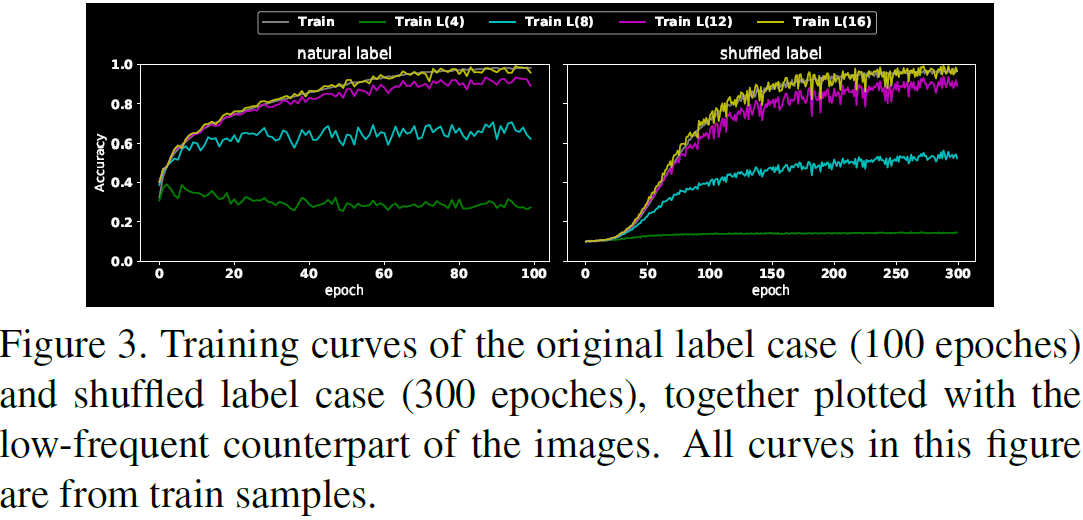
结果绘制在图 3 中。

• 第一个信息是 M_shuffle 需要比 M_natural 更长的训练时间才能达到相同的训练精度（300 个 epoches 与 100 epoches），这表明，相比于学习可泛化的模式，记忆样本是 “不自然” 的行为。
• 通过比较低频训练样本的曲线，我们注意到 M_natural 比 M_shuffle 学习更多的低频模式（即，当 r 为 4 或 8 时）。
• 此外，当 r = 4 时，M_shuffle 几乎没有学习到任何 LFC，而另一方面，即使在第一个 epoch，当 r = 4 时，M_natural 已经学习了大约 40% 的正确 LFC。这种差异表明，当 M_natural 更喜欢选择 LFC，M_shuffle 在 LFC 与 HFC 之间没有偏好。 

如果一个模型可以利用多个不同的信号集，那么为什么 M_natural 更喜欢学习恰好与人类感知偏好一致的 LFC？ 虽然有解释表明神经网络倾向于更简单的功能，但我们推测这仅仅是因为，由于数据集是由人类组织和注释的，因此 LFC-label 组合比 HFC-label 组合更“普遍” ：使用 LFC-label 组合将导致损失的最陡下降，尤其是在训练的早期阶段。

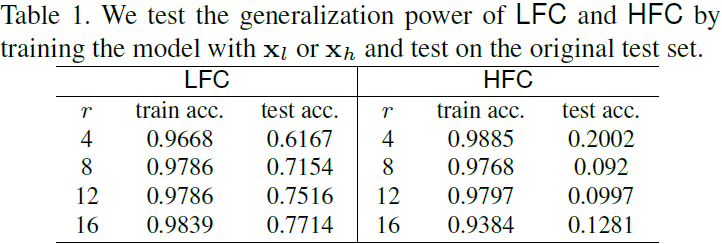
为了验证这个猜想，我们重复 M_natural 的实验，但我们使用 x_l 或 x_h（归一化为标准像素尺度）而不是原始训练集，并测试模型在原始测试集上的表现如何。 表 1 表明 LFC 比 HFC 更 “泛化”。 因此，如果一个模型首先选择 LFC 就不足为奇了，因为它会导致损失最陡下降。

4.3 遗留问题 

最后，我们想提出一个问题：LFC 中的网络偏好与人类感知偏好之间的巧合，可能是许多技术在攀登最先进阶梯的过程中，发明的 “幸存偏差” 的简单结果。 换句话说，神经网络近 100 年的发展过程就像技术的 “自然选择”。 幸存下来的想法可能恰好符合人类的喜好，否则可能会因为爬梯不力而连发表都不能。

 然而，一个有趣的问题是这些爬梯技术与人类视觉偏好的一致性如何。 我们提供使用我们的频率工具评估这些技术。

5. 训练启发式（Heuristics）

我们继续重新评估有助于攀登最先进准确性阶梯的启发式方法。 我们评估这些启发式方法以测试对 LFC 和 HFC 的泛化性能。 准确性阶梯中的许多著名技术似乎或多或少地利用了 HFC。

5.1 不同启发式的比较

我们通过检查 LFC 和 HFC 的预测准确性来测试多种启发式方法，并在训练过程中选择 r 并绘制训练曲线。

Batch 大小：我们研究 batch 大小的选择如何影响泛化行为。 我们在图 4 中绘制了结果。

• 较小的 batch 似乎在提高训练和测试准确性方面表现出色，而较大的 batch 似乎在缩小泛化差距（训练集与测试集性能差距）方面表现突出。
• 此外，泛化差距似乎与模型捕获 HFC 的趋势密切相关：使用较大的 batch 训练的模型对 HFC 更具不变性，并且训练准确性和测试准确性的差异较小。观察到的关系是直观的，因为一旦模型表现得像人一样（因为注释数据的是人），就会实现最小的泛化差距。

图 4 中的观察结果也参与了上一节中关于“可泛化” 特征的讨论。 直观地，更大的 batch，可以导致损失最陡下降的特征更有可能是数据的“可泛化”模式，即 LFC。 

启发式：我们还测试了不同的训练方法对 LFC 和 HFC 的反应，包括：

• Dropout：一种在训练过程中随机降低权重的启发式方法。 我们在 p = 0.5 的全连接层上应用 dropout。
• Mix-up：一种在训练过程中线性整合样本及其标签的启发式方法。 我们使用标准超参数 α = 0.5 来应用它。
• BatchNorm：一种对每个训练小批量执行归一化以加速深度网络训练过程的方法。 它允许我们使用更高的学习率并减少过度拟合，类似于 Dropout。 我们通过将比例 γ 设置为 1 并将偏移量 β 设置为 0 来应用它。
• Adversarial Training：通过一个威胁模型（threat model）在训练期间生成的对抗性示例来增强数据的方法。 它被广泛认为是最成功的对抗鲁棒性（防御）方法之一。 按照流行的选择，我们使用 ε = 8/255 (ε = 0.03 ) 的 PGD 作为威胁模型。

我们在图 5 中说明了结果，其中第一个图是原始设置，然后在余下四个图中测试了四种启发式方法中的每一种。 

• 在我们的实验中，Dropout 的行为与普通设置大致相似。
• Mix-up 提供了类似的预测精度，但是，它捕获了更多的 HFC，这可能并不奇怪，因为 mix-up 增强不会明确鼓励任何关于 LFC 的信息，并且性能提升可能是由于对 HFC 的关注。
• 对抗性训练（Adversarial Training）的行为大多符合预期：它报告的预测准确性较低，这可能是由于鲁棒性和准确性之间的权衡。 它还报告了一个较小的泛化差距，这可能是由于选择了“可泛化”模式的结果，正如其对 HFC 的不变性所证实的那样（例如，r = 12 或 r = 16）。 然而，当 r = 4 时，对抗训练似乎对 HFC 很敏感，即使是普通设置也忽略了这一点。
• BatchNorm 的性能值得注意：与 vanilla 设置相比，BatchNorm 在 LFC 和 HFC 中都选择了更多信息，尤其是当 r = 4 和 r = 8 时。这种 BatchNorm 在捕获 HFC 方面的倾向也与 BatchNorm 鼓励对抗脆弱性有关。

其他测试：我们还测试了其他启发式或方法，仅沿一个维度进行更改，而其余部分与第 4 节中的原始设置相同。

模型架构：我们测试了 LeNet 、AlexNet 、VGG 和 ResNet。 ResNet 体系结构似乎在不同级别上优于以前的发明：它报告了更好的原始设置测试准确性、更小的泛化差距（训练和测试准确性之间的差异）以及捕获 HFC 的趋势较弱。

优化器：我们测试了 SGD、ADAM、AdaGrad、AdaDelta 和 RMSprop。 我们注意到 SGD 似乎是唯一一个具有明显捕获 HFC 的趋势，而其余的在我们的实验中是相同的。

5.2 关于批量归一化的假设

基于观察，我们假设 BatchNorm 的优势之一是通过归一化来对齐不同预测信号的分布差异。 例如，HFC 通常显示出比 LFC 更小的幅度，因此在没有 BatchNorm 的情况下训练的模型可能不容易拾取这些 HFC。 因此，较高的收敛速度也可以认为是同时捕获不同预测信号的直接结果。

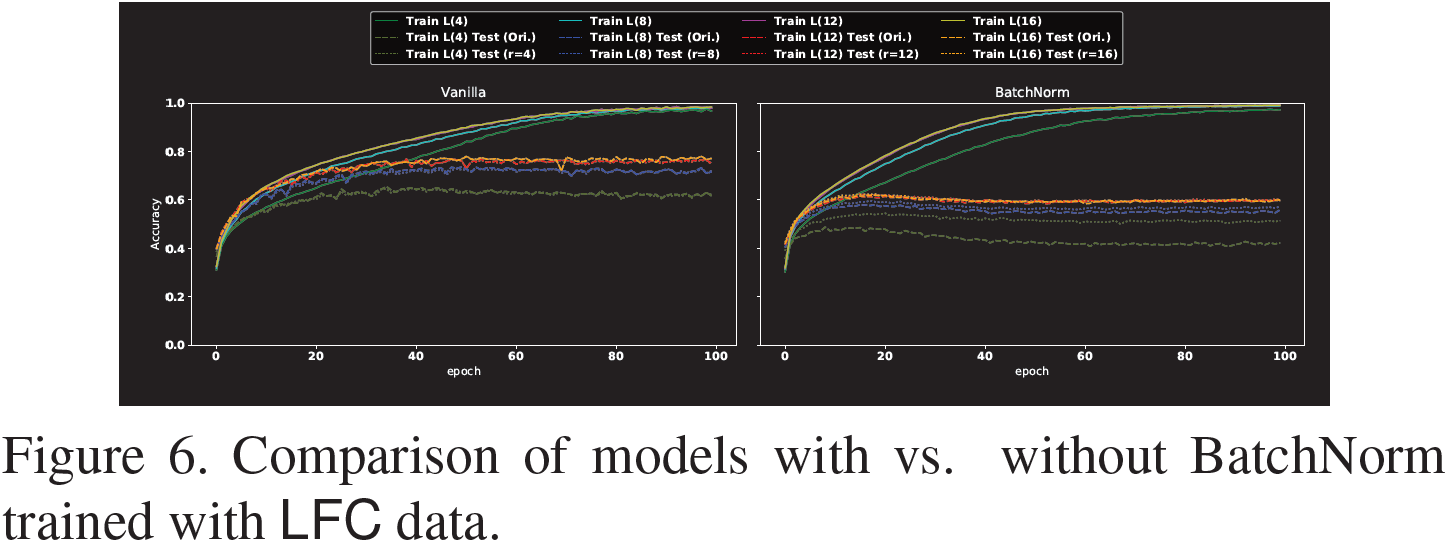
为了验证这一假设，我们比较了使用 BatchNorm 与未使用 BatchNorm 训练的模型在 LFC 数据上的性能，并将结果绘制在图 6 中。

如图 6 所示，当仅使用 LFC 训练模型时，BatchNorm 并不总是有助于提高预测性能，无论是通过原始数据还是通过相应的 LFC 数据进行测试。 此外，半径越小，BatchNorm 的帮助就越小。 此外，在我们的设置中，BatchNorm 的泛化效果不如原始设置，这可能会引发有关 BatchNorm 优势的问题。 

然而，BatchNorm 似乎仍然至少提高了训练准确性的收敛性。 有趣的是，当 r = 4 时加速度最小。这一观察进一步符合我们的假设：如果 BatchNorm 的优势之一是鼓励模型捕获不同的预测信号，那么当 r = 4 时使用 LFC 训练模型时，BatchNorm 的性能增益是最有限的 。

6. 对抗性攻防

正如人们可能注意到的那样，我们对 HFC 的观察可以直接与“对抗性示例”现象联系起来：如果预测依赖于 HFC，那么 HFC 的扰动将显着改变模型的响应，但人类可能无法观察到这种扰动，导致了神经网络的非直觉行为。

本节致力于研究对抗鲁棒性和模型利用 HFC 的趋势之间的关系。

6.1 内核平滑度与图像频率

正如卷积定理所述，图像的卷积运算等价于图像频域的乘法。 因此，粗略地说，如果一个卷积核在频域高端的权重可以忽略不计，它就会相应地对 HFC 进行加权。 这可能只适用于第一层的卷积核，因为更高层的核不直接与数据相关，因此关系不明确。

因此，我们认为，要推动模型忽略 HFC，可以考虑强制模型学习在频域高端仅具有可忽略权重的卷积核。

直观上（根据信号处理知识），如果卷积核是“光滑”的，即相邻权重之间没有剧烈波动，则相应的频域将看到可以忽略不计的高频信号。 这些联系已在数学上得到证明，但这些已证明的确切关系超出了本文的范围。

6.2 稳健的模型具有光滑的内核

为了理解 “平滑度” 和对抗鲁棒性之间的联系，我们在图 7 (a) 和 (b) 中可视化了以普通方式 (M_natural) 和对抗方式 (M_adversarial) 训练的模型的第一层的卷积核 。

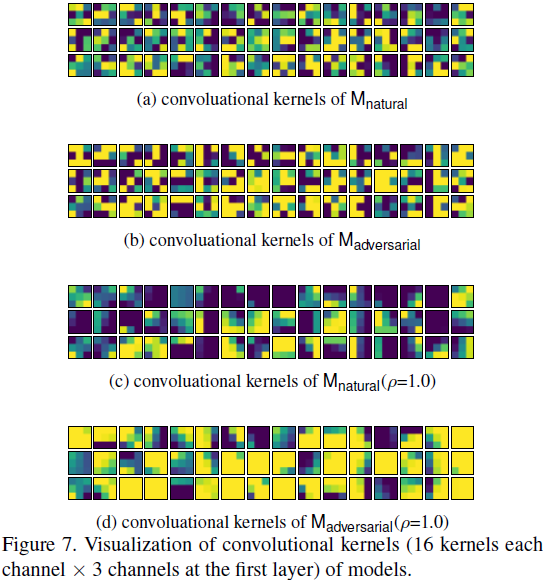
比较图 7(a) 和图 7(b)，我们可以看到 Madversarial 的内核倾向于显示更平滑的图案，这可以通过 M_adversarial 内核的相邻权重倾向于共享相同的颜色来观察。 可视化可能不是很清楚，因为 ResNet 中的卷积核只有 [3 × 3]，当第一层具有大小为 [5 × 5] 的卷积核时，在附录中使用其他架构可以更清楚地传递消息。.

6.3 平滑内核提高了对抗鲁棒性 

6.1 中的直观论证和 6.2 中的实证结果直接引出了一个问题，即我们是否可以通过平滑第一层的卷积核来提高模型的对抗鲁棒性。

在讨论之后，我们介绍了一种极其简单的方法，该方法似乎可以提高针对 FGSM 和 PGD 的对抗鲁棒性。 对于卷积核 w，我们使用 i 和 j 来表示它的列和行索引，因此 w_i,j 表示第 i 行和第 j 列的值。 如果我们使用 N(i, j) 来表示 (i, j) 的空间邻居集，我们的方法很简单：

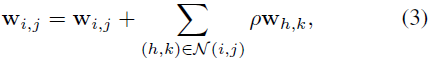
其中 ρ 是我们方法的超参数。 我们固定 N(i, j) 有八个邻居。 如果 (i, j) 在边缘，那么我们只需复制边界上的值即可生成边界外值。

换句话说，我们试图通过混合相邻值来简单地减少相邻差异来平滑内核。 该方法几乎没有任何计算负载，但似乎提高了 M_natural 和 M_adversarial 对 FGSM 和 PGD 的对抗鲁棒性，即使当 M_adversarial 以 PGD 作为威胁模型进行训练时也是如此。 

在图 7 中，我们将卷积核与我们的方法应用于 ρ = 1.0 的 M_natural 和 M_adversarial 可视化，分别表示为 M_natural (ρ = 1.0) 和 M_adversarial (ρ = 1.0)。 如可视化所示，生成的内核往往会显示出明显更平滑的模式。

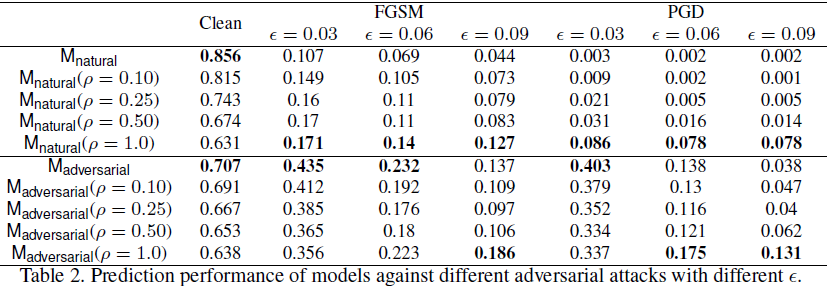
我们测试了通过我们的方法平滑的模型针对 FGSM 和 PGD 的鲁棒性，选择不同的 ε，其中最大扰动为 1.0。如表 2 所示，

• 当应用我们的平滑方法时，纯净 (clean) 精度直接下降，但对抗鲁棒性有所提高。特别是，当允许扰动相对较大时，我们的方法会有所帮助。 例如，当 ε = 0.09（大约 23/255）时，M_natural (ρ = 1.0) 甚至优于 M_adversarial。
• 总的来说，我们的方法可以很容易地提高 M_natural 的对抗鲁棒性，但只能在 ε 较大的情况下对 M_adversarial 进行改进，这可能是因为 M_adversarial 是以 PGD (ε = 0.03) 作为威胁模型进行训练的。 

7. Beyond 图像分类

我们的目标不仅仅是探索图像分类任务。 我们调查对象检测任务。 我们使用 RetinaNet 和 ResNet50 + FPN 作为主干。 我们使用 COCO 检测训练集训练模型，并在其包含 5000 张图像的验证集中执行推理，并实现 35.6% 的均值平均精度（Mean Average Precision，MAP）。

然后我们选择 r = 128 并将图像映射到 x_l 和 x_h 并使用相同的模型进行测试，得到 27.5% MAP 的 LFC 和 10.7% MAP 的 HFC。 从 35.6% 到 27.5% 的性能下降引起了我们的兴趣，因此我们进一步研究是否应该预期人类也会出现同样的下降。

7.1 LFC 性能下降

从 x 到 x_l 的性能下降可能是预料之中的，因为当 HFC 被丢弃时 x_l 可能没有来自原始图像的丰富信息。 特别是，与图像分类不同，HFC 可能在描绘某些对象（尤其是较小的对象）方面发挥重要作用。

图 8 说明了一些示例，其中当输入图像被低频对应图像替换时，识别某些对象的效果更差。 这种差异可能是预料之中的，因为低频图像往往是模糊的，而且一些物体对人类来说可能也看不清。 

7.2 LFC 的性能提升 

然而，当我们从相反的方向检查性能差距时，差异会变得有趣。 我们确定了 1684 张图像，对于这些图像中的每一张，与原始图像相比，一些对象被识别得更好（高 MAP 分数）。

结果显示在图 9 中。似乎没有明显的原因说明为什么这些对象在人为检查时在低频图像中被更好地识别。 这些观察结果加强了我们的论点，即 CNN 与人类之间的感知差异也存在于图像分类以外的更高级的计算机视觉任务中。

8. 讨论：HFC 只是噪音吗？ 

为了回答这个问题，我们尝试了另一种常用的图像去噪方法：截断奇异值分解 (SVD)。 我们分解图像并将图像分离为一个具有主导奇异值（dominant singular values）的重建图像和一个具有尾随奇异值（trailing singular values）的重建图像。 通过这种设置，我们发现支持图 2 现象的图像要少得多。我们的观察表明，CNN 利用的 HFC 不仅仅是随机“噪声”。

9. 结论与展望

我们研究了图像频谱如何影响 CNN 的泛化行为，从而从一个新的角度对神经网络的泛化行为进行了多种有趣的解释：数据中存在多个信号，但并非所有信号都符合人类的视觉偏好。 由于本文全面涵盖了许多主题，我们简要重申所学到的主要经验教训：

• CNN 可能会捕获与人类视觉偏好 (§3) 不一致的 HFC，从而导致泛化之谜，例如学习标签随机化数据的悖论 (§4) 和对抗脆弱性 (§6)。
• 提高准确性的启发式方法（例如 Mix-up 和 BatchNorm）可能会鼓励捕获 HFC (§5)。 由于准确性和鲁棒性之间的权衡（§3），我们可能不得不重新考虑它们的价值。
• 对抗性强的模型往往具有平滑的卷积核，反之并不总是正确的（§6）。
• 在目标检测 (§7) 的上下文中注意到了类似的现象，但还有更多的结论有待得出。

展望未来，我们希望我们的工作能够成为对未来计算机视觉研究时代的呼唤，在这个时代，最先进的技术并不像我们想象的那么重要。

• 排行榜上的单个数字虽然可以显着推动研究朝着一个方向发展，但并不能可靠地反映模型与人类之间的一致性，而这种一致性可以说是最重要的。
• 我们希望我们的工作将朝着一个新的测试场景出发，在这个场景中，低频对应的性能需要与原始图像的性能一起报告。
• 考虑到人类如何看待数据的显式归纳偏差可能在未来发挥重要作用。 特别是，神经科学文献表明，人类倾向于依赖低频信号来识别物体，这可能会激发未来方法的发展。

参考

Wang H, Wu X, Huang Z, et al. High-frequency component helps explain the generalization of convolutional neural networks[C]//Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020: 8684-8694.

[27] Andrew Ilyas, Shibani Santurkar, Dimitris Tsipras, Logan Engstrom, Brandon Tran, and Aleksander Madry. Adversarial examples are not bugs, they are features. arXiv preprint arXiv:1905.02175, 2019.

S. 总结

S.1 核心思想

本文研究图像频谱与 CNN 泛化能力之间的关系。作者认为，CNN 的非直觉泛化行为是人类与模型之间感知差异的直接结果：CNN 可以捕捉到人类无法察觉的高频分量。

S.2 研究方法

结合使用傅里叶变换和滤波器，获得图像的低频分量（LFC）和高频分量（HFC）。然后，使用傅里叶逆变换对分量进行重建，使用这些重建图像作为测试集验证模型的精度。

请注意，傅里叶变换或其逆变换可能会引入复数。在本文中，简单地丢弃了傅里叶逆变换结果的虚部，以确保生成的图像可以像往常一样输入 CNN。

S.3 分析

研究表明，CNN 更喜欢学习恰好与人类感知偏好一致的 LFC。虽然有解释表明神经网络倾向于更简单的功能，但作者推测这是因为，由于数据集是由人类组织和注释的，因此数据集中 低频-标签 组合比 高频-标签 组合更“普遍”。

本文我赞同的一段话“最后，我们想提出一个问题：LFC 中的网络偏好与人类感知偏好之间的巧合，可能是许多技术在攀登最先进阶梯的过程中，发明的 “幸存偏差” 的简单结果。 换句话说，神经网络近 100 年的发展过程就像技术的 “自然选择”。 幸存下来的想法可能恰好符合人类的喜好，否则可能会因为爬梯不力而连发表都不能。”

S.4 启发式

作者研究不同启发式对泛化性能的影响。这里只列出来影响显著的两个。

Batch 大小。较大的 batch 有较小的泛化差距，而此时，模型学到的高频成分并不多。观察到的关系是直观的，因为一旦模型表现得像人一样（注释数据的是人，人无法观察高频成分），就会实现最小的泛化差距。

BatchNorm。 在有 BatchNorm 的条件下，模型可以利用更多的高频成分。BatchNorm 的优势之一是通过归一化来对齐不同预测信号的分布差异。 例如，HFC 通常显示出比 LFC 更小的幅度，因此在没有 BatchNorm 的情况下训练的模型可能不容易拾取这些 HFC。

S.5 稳健性与卷积核平滑度

稳健性强的模型往往具有平滑的卷积核。如果模型通过高频分量进行预测，那么对高频分量的微小扰动就会对模型结果产生巨大影响。

如果卷积核是“光滑”的，即相邻权重之间没有剧烈波动，则相应的频域将看到可以忽略不计的高频信号。

使用平滑的卷积核，虽然会影响模型精度，但是可以提升稳健性。