前言

散列表是一种常用的数据结构，它可以快速地存储和查找数据。散列表的基本思想是，将数据的关键字映射到一个有限的地址空间中，然后在该地址空间中存储数据。这样，当需要查找某个数据时，只需要计算其关键字的映射地址，然后在该地址处访问数据，从而实现高效的查找操作。

一、设计思想

散列表的核心是散列函数，也称为哈希函数。散列函数的作用是，将任意长度的关键字转换为一个固定长度的地址，这个地址就是散列值或哈希值。散列函数应该满足以下几个要求：

• 一致性：相同的关键字应该产生相同的散列值。

• 高效性：散列函数的计算应该简单快速，不占用过多的时间和空间。

• 均匀性：散列函数应该尽可能地将关键字均匀地分布在地址空间中，避免产生冲突。冲突是指不同的关键字映射到相同的地址的情况，这是不可避免的。因此，散列表还需要一个解决冲突的方法。常用的解决冲突的方法有两种：

• 开放寻址法：当发生冲突时，按照某种规则在地址空间中寻找下一个空闲的位置，直到找到或者遍历完整个地址空间为止。这种方法需要保证地址空间有足够的容量，否则会导致插入失败或者查找效率降低。

• 链地址法：当发生冲突时，将具有相同地址的数据组织成一个链表，每个地址处只存储链表的头指针。这种方法不受地址空间大小的限制，但是需要额外的空间存储链表节点。

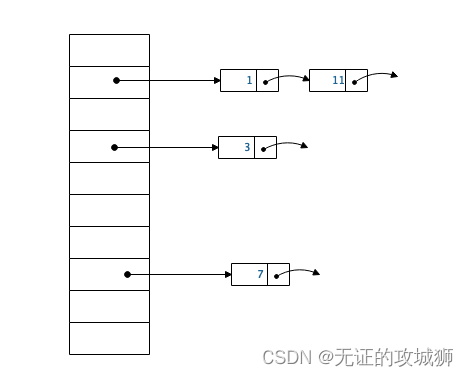
下面我们用C++实现一个简单的散列表，采用除留余数法作为散列函数，采用链地址法作为解决冲突的方法。除留余数法是指，将关键字除以一个素数p，然后取余数作为散列值。我们假设关键字是整数类型，素数p是10（也可以不是素数，但因为不是素数能被更多的数整除，冲突概率大，所以文中用了1，3，7，11做演示），地址空间大小也是10。

二、实现步骤

首先，我们定义一个链表节点类Node，用来存储数据和指向下一个节点的指针：

1、定义节点

这是一个链表的节点定义，它的作用是存储同一hash值（也叫散列值）的数据，所以它有next指向下一个节点，从设计思想来看，hash函数设计得越好，这个单向链表越短，那么效率就越高。最差情况当然就是所有的数据经过hash函数计算后的值都一样，那就成了一个单向链表，这种情况是一定要避免的。

class Node{
	public:
		int key;        //键
		int value;      //值
		Node* next;            //指向下一个结点的指针
		Node(int k, int v){    //构造函数
			key = k;
			value = v;
			next = nullptr;
		}
};

2、定义Hash表类

然后我们定义一个散列表类，用来管理结点和提供基本的操作：
int hash(int key)，这个就是散列函数，它只简单计算了余数。对于散列函数来说，应在hash值尽量分布均匀的基础上设计简单点，不然把大把时间都花在计算hash值上了。这里是以整数作为例子的，所以直接模运算了，实际泛型编程要考虑其它类型数据的hash值计算。

class HashTable{
	private:
		int capacity;   //数组的容量
		int size;       //当前存储的键值对的数量
		Node** array;   //指向数组的指针
		int hash(int key){    //散列函数，简单地取模
			return key % capacity;
		}
		
	public:
		HashTable(int c){   //构造函数，初始化数组和其他变量
			capacity = c;
			size = 0;
			array = new Node*[capacity];
			for (int i = 0; i < capacity; i++){
				array[i] = nullptr;
			}
		}
		
		~HashTable(){       //析构函数，释放内存
			for (int i = 0; i < capacity; i++){
				Node* cur = array[i];
				while (cur != nullptr){
					Node* next = cur->next;
					delete cur;
					cur = next;
				}
			}
			delete[] array;
		}

以上代码定义了散列表，就是一个构造函数和析构函数，比较简单。有一定C++语言基础的都能看明白，既然来看这篇文章了，肯定是有C++基础的。

Node** array; //指向数组的指针 这是一个二级指针，指向一个存放指针的数组。这个数组的下标就是我们hash计算的目标。这个数组中存放了每个链表的链表头节点。

		
	    void insert(int key, int value){      //插入操作
	        int index = hash(key);           //计算键对应的位置
	        Node* cur = array[index];        //获取该位置的链表头结点
	        while (cur != nullptr){         //遍历链表，查找是否已经存在相同的键
	            if (cur->key == key){       //如果存在，更新值并返回
	                cur->value = value;
	                return;
	            }
	            cur = cur->next;
	        }
	        //如果不存在，创建新的结点，并插入到链表头部
	        Node* newNode = new Node(key, value);
	        newNode->next = array[index];
	        array[index] = newNode;
	        size++;          //更新键值对数量
	    }
    
	    int get(int key){          //查找操作
	        int index = hash(key);    //计算键对应的位置
	        Node* cur = array[index];  //获取该位置的链表头结点
	        while (cur != nullptr){      //遍历链表，查找是否存在相同的键
	            if (cur->key == key){    //如果存在，返回值
	                return cur->value;
	            }
	            cur = cur->next;
	        }
	        //如果不存在，返回-1表示错误
	        return -1;
	    }

以上是插入、取值的操作，具体看注释就明白实现过程了。
以下是删除键值对的方法，因为实际存储数据是单向链表，所以删除操作时要记录上一个节点的指针，略微麻烦一点。

	    void remove(int key){      //删除操作
	        int index = hash(key);    //计算键对应的位置
	        Node* cur = array[index];   //获取该位置的链表头结点
	        Node* prev = nullptr;       //记录前一个结点的指针
	        while (cur != nullptr) {    //遍历链表，查找是否存在相同的键
	            if (cur->key == key){      //如果存在，删除结点，并更新链表和数组
	                if (prev == nullptr){     //如果是头结点，直接更新数组
	                    array[index] = cur->next;
	                } else {                 //如果不是头结点，更新前一个结点的指针
	                prev->next = cur->next;
	                }
	                delete cur;       //释放内存
	                size--;           //更新键值对数量
	                return;
	            }
	            prev = cur;         //更新前一个结点的指针
	            cur = cur->next;       //移动到下一个结点
	        }
	        //如果不存在，不做任何操作
	    }
};

以上是具体功能实现的函数，和前面链表的功能有很多相似之处。加上代码的详细注释，相信是很容易看明白的。流程很简单，根据传入的 key ，用 hash 函数计算得到一个值，因为是模运算，这个值肯定在0到9之间（这里以10为例，事实上也可以是任何其它正整数），就以这个余数作为arrary数组的下标，这个数组中存储的又是一个单向链表的头节点。我们就到这个链表中去具体匹配是哪个节点进行增加删除工作。

三、数据示例

以上就是我们用C++实现的散列表类。我们可以用以下代码测试它的功能：

#include <iostream>
using namespace std;

int main(){
    HashTable ht(13); // 创建一个容量为10的散列表对象

	ht.insert(1, 10); // 插入一些键值对
	ht.insert(7, 20);
	ht.insert(3, 30);
	ht.insert(11, 110);

	cout << ht.get(1) << endl; // 查找一些键，并打印结果
    cout << ht.get(7) << endl;
	cout << ht.get(3) << endl;
	cout << ht.get(11) << endl;

	ht.remove(2); // 删除一个键

	cout << ht.get(2) << endl; // 再次查找该键，并打印结果

	return 0;
}

输出结果如下：

10
20
30
110
-1

根据程序设计，要求“键”和“值”都是整数。所以我们传入的参数是两个整数。ht.insert(1, 10); // 插入一些键值对，这里的参数1是作为key的，参数10是作为value的。散列表还有个不正规的名字叫“键值对”。它是根据“键”去确定“值”存储位置的，当然也根据“键”去取“值”。设计优秀的散列表存取速度是很快的。它和数据库的设计思想是有相通之处的。所以在示例中，和图上画的一样，“key”：1 和“key”：11 都是存在下标为1的数组指针指向的链表，根本不存在下标为11的情况。而ht.get(2)hash计算的结果是2，数组下标2是空指针，所以输出是-1。

总结

可以看到，我们实现的散列表可以正确地执行插入、查找和删除操作。当然，这只是一个简单的示例，实际上还有很多细节和优化可以考虑。例如，如何选择合适的散列函数和容量？如何动态地调整容量？如何处理负数或其他类型的键？如何提高代码的可读性和可维护性？等等。这些问题都可以作为进一步学习和探索的方向。