您现在的位置是:首页 >技术教程 >华为FinalMLP网站首页技术教程
华为FinalMLP
FinalMLP:An Enhanced Two-Stream MLP model for CTR Prediction
摘要
Two-Stream model:因为一个普通的MLP网络不足以学到丰富的特征交叉信息,因此大家提出了很多实用MLP和其他专用网络结合来学习。
MLP是隐式地学习特征交叉,当前很多工作主要在另外一个stream中显式的增强特征交叉。本文提出的两个stream都用MLP网络,训练的好一样能达到惊人的效果。而且提出的可插拔式使用的特征选择层和交叉融合层,可以得到性能更强的two-stream MLP模型。
简介
单个MLP网络很难学到丰富的特征交叉信息。很多模型结构提出了是为了学习显式的特征交叉,像FM、CIN、AFN,虽然这些模型能很好学习到一阶、二阶、三阶等交叉特征,但是没法像MLP网络学到深层次交叉信息,因此很多two-stream的模型提出了,结合MLP网络和显式交叉网络,结合两者优点,像Wide&Deep、DeepFM、DCN、xDeepFM、AutoInt+,这些two-stream模型中,MLP网络学习隐式的特征交叉,另外一个stream学习显式的特征交叉。
很多two-stream模型都验证了对于单个MLP网络的效果,但是没有对比过结合两个MLP网络的two-stream模型(称为DualMLP),本文就做了对比,尽管DualMLP结构很简单,但是效果惊人。
two-stream模型可以视作两个并行网络的集成,每个stream可以从不同视角学到特征交叉的信息。比如Wide&Deep、DeepFM,一个stream去学习低阶的特征交叉,另外一个stream学习高阶的特征交叉;DCN、AutoInt+一个stream去学习显式的特征交叉,另外一个stream学习隐式的特征交叉;xDeepFM进一步从vector-wise和bit-wise视角学习特征交叉。这些都验证了两个stream中网络的差异对效果有重要影响。
本文的two-stream中两个stream都是MLP网络,差异性在于网络的层数和隐层单元数,实验发现可以实现更好的效果。同时将DualMLP作为base,在此基础上面增大两个stream的差异性,可以进一步提升DualMLP的效果。当前的two-stream模型在结合两个stream的时候通过sum或者concat,这个简单操作可能浪费了更高水平交叉(stream-level)的机会。
FinalMLP:intergrates Feature selection and interaction aggregation layers on top of two MLP module networks。即结合了特征选择层和交叉融合层的双流MLP网络,特征选择层是通过gate网络得到特征重要性进行soft特征选择,每个stream通过选择不同重要度的特征,增大各个stream的差异性。交叉融合层则是提出了一个二阶的双线性融合融合,同时为了减低计算复杂度,将计算分成k个组,也就是多头双线性融合。
背景及相关工作
Framework of Two-Stream CTR Models
框架图
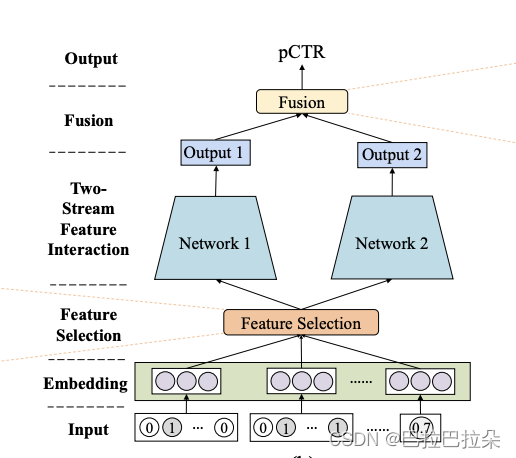
特征Embedding
高维稀疏到稠密的表示
特征选择
可选的层,本文提出的是软选择,通过特征的重要性权重选择
特征交叉
通过两个不同的并行的网络进行交叉
两个网络的融合(Stream-level Fusion)
假设最后预估的概率为
y
^
hat y
y^,
o
1
mathbf o_1
o1和
o
2
mathbf o_2
o2是两个stream的输出表示,
F
mathcal{F}
F表示融合操作,通常是sum或者concat。
w
w
w表示将输出映射成一维的线性函数。
y
^
=
σ
(
w
T
F
(
o
1
,
o
2
)
)
hat y = sigma (w^T mathcal{F} (mathbf o_1, mathbf o_2))
y^=σ(wTF(o1,o2))
代表性的Two-Stream CTR Models
Wide&Deep:一个线性网络(line stream)和一个MLP网络(deep stream)
DeepFM:在wide侧用FM替换,二阶显式交叉
DCN:一个cross网络做高阶显式交叉,另外一个stream是MLP做隐式交叉
xDeepFM:使用CIN通过vector-wise方式高阶交叉,另外一个stream通过bit-wise方式隐式交叉
AutoInt+:使用自注意力网络学习高阶交叉,融合AutoInt和MLP作为two-stream
AFN+:融合AFN和MLP作为two-stream
DeepIM:一个交互机器组件IM(interaction machine module)学习高阶特征交叉,融合IM和MLP作为two-stream
MaskNet:使用两个MaskNet作为two-stream
DCN-V2:通过一个更具表现力的cross网络来做显式特征交叉,使用cross网络和MLP作为two-stream
EDCN:并不是严格的two-stream模型,提出的一个桥接模块,桥接两个stream隐层的,这个操作限制每个stream的隐层必须有相同的层数和神经单元数,降低了灵活性
Two-Stream MLP Model
本文提出的两个stream都是MLP,称为DualMLP,两个MLP网络(隐层数及unit数不同)表示如下
o
1
=
M
L
P
1
(
h
1
)
mathbf o_1 = MLP_1(mathbf h_1)
o1=MLP1(h1)
o
2
=
M
L
P
1
(
h
2
)
mathbf o_2 = MLP_1(mathbf h_2)
o2=MLP1(h2)
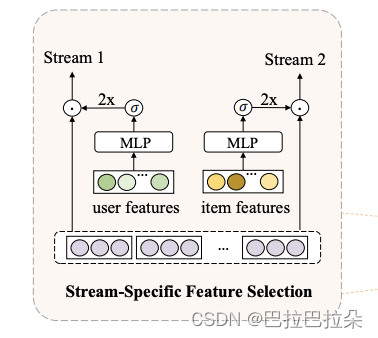
Stream-Specific Feature Selection
受MMoE启发,每个stream根据gate网络对特征进行差异化选择,特征选择层定义如下
g
1
=
G
a
t
e
1
(
x
1
)
,
g
2
=
G
a
t
e
1
(
x
2
)
mathbf g_1 = Gate_1(mathbf x1), mathbf g_2 = Gate_1(mathbf x2)
g1=Gate1(x1),g2=Gate1(x2)
h
1
=
2
σ
(
g
1
)
⊙
e
,
h
2
=
2
σ
(
g
2
)
⊙
e
mathbf h_1 = 2 sigma(mathbf g_1) odot mathbf e, mathbf h_2 = 2 sigma(mathbf g_2) odot mathbf e
h1=2σ(g1)⊙e,h2=2σ(g2)⊙e
这里
G
a
t
e
i
Gate_i
Gatei表示stream中MLP基于的门控网络,是以选择的特征集
x
i
mathbf x_i
xi作为输入,两个stream的输入可以是不同的特征子集。输出是各个特征的权重
g
i
mathbf g_i
gi,这里乘以2主要是为了权重均值为1。
下面有个示例图,输入分别是user、item特征集
交叉融合Stream-Level Interaction Aggregation
Bilinear Fusion
当前都是sum或者concat融合,借鉴在CV领域广泛使用的双线性pooling,提出双线性交叉融合层,去融合两个stream的输出,表示如下
y
^
=
σ
(
b
+
w
1
T
o
1
+
w
2
T
o
2
+
o
1
T
W
3
o
2
)
hat y = sigma (b + mathbf w_1^T mathbf o_1 + mathbf w_2^T mathbf o_2 + mathbf o_1^T mathbf W_3 mathbf o_2)
y^=σ(b+w1To1+w2To2+o1TW3o2)
其中,
b
∈
R
,
w
1
∈
R
d
1
×
1
,
w
2
∈
R
d
2
×
1
W
3
∈
R
d
1
×
d
2
bin R,mathbf w_1 in R^{d_1 imes 1}, mathbf w_2 in R^{d_2 imes 1} mathbf W_3 in R^{d_1 imes d_2}
b∈R,w1∈Rd1×1,w2∈Rd2×1W3∈Rd1×d2,这里
d
1
d_1
d1和
d
2
d_2
d2表示
o
1
mathbf o_1
o1和
o
2
mathbf o_2
o2的维度。
o 1 T W 3 o 2 mathbf o_1^T mathbf W_3 mathbf o_2 o1TW3o2表示 o 1 mathbf o_1 o1和 o 2 mathbf o_2 o2二阶双线性交叉,当 W 3 mathbf W_3 W3是单位矩阵,那就是点乘,如果是零矩阵,就是concat融合( b + [ w 1 , w 2 ] T [ o 1 , o 2 ] b+[mathbf w_1, mathbf w_2]^T[mathbf o_1, mathbf o_2] b+[w1,w2]T[o1,o2])
这个双线性融合和FM也有关联,FM,使用
m
m
m维的特征向量
x
mathbf x
x建模二阶交叉,可以表示为
y
^
=
σ
(
b
+
w
T
x
+
x
T
u
p
p
e
r
(
P
P
T
)
x
)
hat y = sigma (b + mathbf w^T mathbf x + mathbf x^T mathcal{upper} (mathbf P mathbf P^T) mathbf x)
y^=σ(b+wTx+xTupper(PPT)x)
其中, b ∈ R , w ∈ R m × 1 , P ∈ R m × d bin R,mathbf w in R^{m imes 1}, mathbf P in R^{m imes d} b∈R,w∈Rm×1,P∈Rm×d,其实FM是双线性融合的特例,当 o 1 = o 2 mathbf o_1 = mathbf o_2 o1=o2
但是这么做有个缺点,当 o 1 mathbf o_1 o1和 o 2 mathbf o_2 o2维度较大时,例如1000维,双线性映射矩阵 W 3 ∈ R 1000 × 1000 mathbf W_3in R^{1000 imes 1000} W3∈R1000×1000参数量太大。
多头双线性融合
借鉴多头注意力的思想,将
o
1
mathbf o_1
o1和
o
2
mathbf o_2
o2拆分为
k
k
k个子空间
o
1
=
[
o
11
,
o
12
,
.
.
.
,
o
1
k
]
mathbf o_1 = [mathbf o_{11}, mathbf o_{12}, ..., mathbf o_{1k}]
o1=[o11,o12,...,o1k]
o
2
=
[
o
21
,
o
22
,
.
.
.
,
o
2
k
]
mathbf o_2 = [mathbf o_{21}, mathbf o_{22}, ..., mathbf o_{2k}]
o2=[o21,o22,...,o2k]
k
k
k是超参数,在各个子空间分别进行双线性映射
y
^
=
σ
(
∑
j
=
1
k
B
F
(
o
1
j
,
o
2
j
)
)
hat y = sigma ( sum_{j = 1} ^k BF(mathbf o_{1j}, mathbf o_{2j}))
y^=σ(j=1∑kBF(o1j,o2j))
这样就把参数量由
d
1
d
2
d_1d_2
d1d2变为
d
1
d
2
/
k
d_1d_2/k
d1d2/k
模型训练
L = − 1 N ∑ ( y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) ) L = - frac {1} {N} sum(y mathcal log(hat y) + (1-y) mathcal log(1-hat y)) L=−N1∑(ylog(y^)+(1−y)log(1−y^))
实验
模型实现基于FuxiCTR,一个开源的预估CTR库。embedding_size = 10, batch_size = 4096, 默认的MLP层单元数[400, 400, 400]。对于DualMLP和FinalMLP,两个MLP设置1-3层,学习率设置为1e-3或者1e-5。
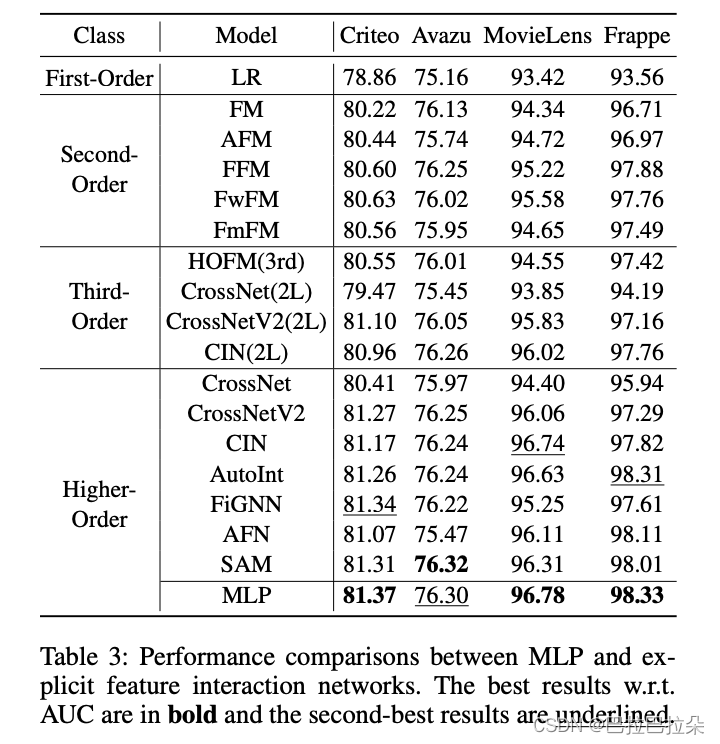
比较单个MLP和显式交叉网络
单个MLP效果非常惊人
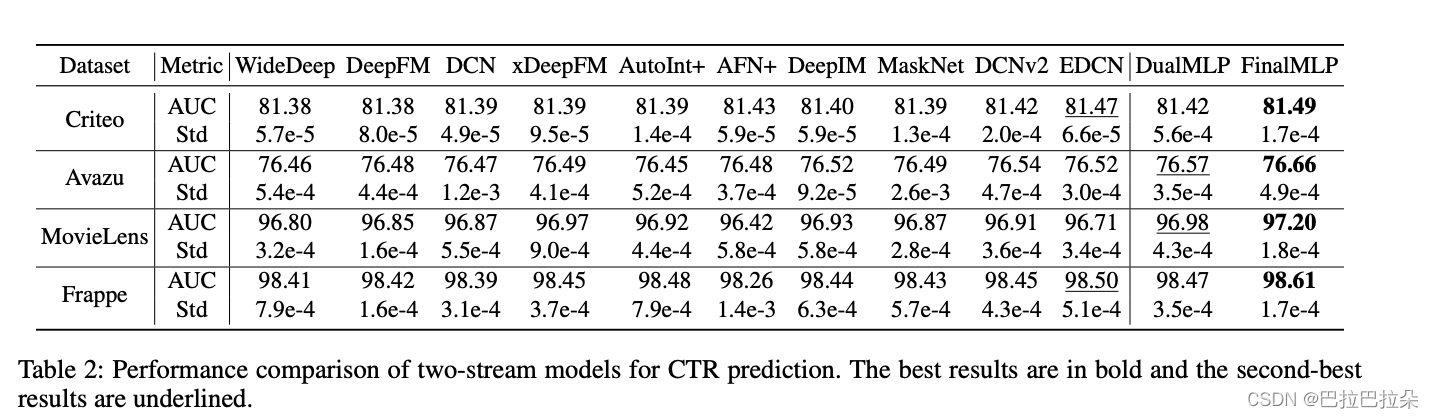
DualMLP和FinalMLP
可以看到在two-stream模型中,DualMLP和FinalMLP效果完胜。
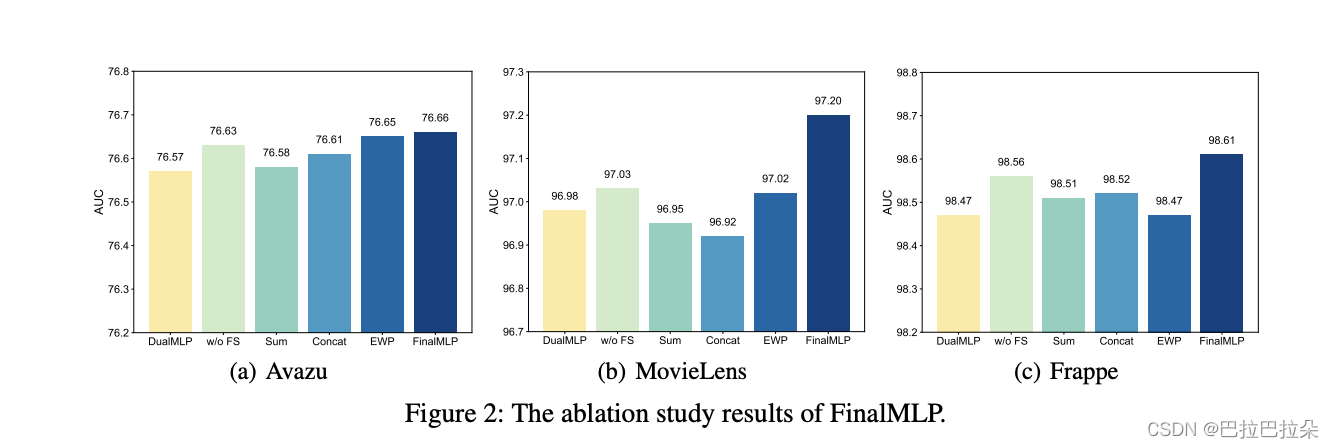
Ablation Studies
对比下面几个模块,说明提出的特征选择层及双线性融合层是有效果的
DualMLP
w/o FS:去掉特征选择模块
Sum:FinalMLP使用sum融合
Concat:FinalMLP使用Concat融合
EWP:FinalMLP使用Elemen-wise乘融合
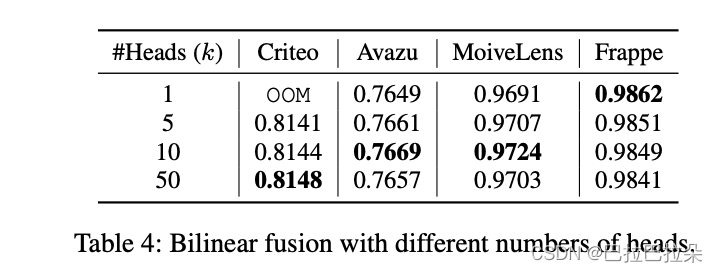
多头双线性融合
拆分为多个子组后,效果更好,但是需要调整超参数
k
k
k.
总结
这个论文仅用MLP网络就实现了这么强的效果,和一般认知还是有些diff的,说明MLP网络只要调整的好,效果也是相当惊人的。






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结