您现在的位置是:首页 >其他 >排序算法:堆排序网站首页其他
排序算法:堆排序
朋友们、伙计们,我们又见面了,本期来给大家解读一下栈和队列方面的相关知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成!
数据结构与算法专栏:数据结构与算法
个 人 主 页 :stackY、
C 语 言 专 栏:C语言:从入门到精通
目录
前言:
通过前面的学习和了解我们了解到了二叉树使用顺序结构实现的方式为堆,并且对堆的实现都做了详细的介绍,那么本期我们来看看堆到底都有哪些应用场景呢?
堆这个数据结构我们经常使用它来进行堆排序和解决Top-K的问题,本期我们先来重点的了解堆是怎么进行排序的呢?
1.堆的应用:堆排序
前面我们讲到过冒泡排序和qsort排序,那么本期再来一种新的排序算法,它的效率也是蛮高的。它所要用到的相关知识点就是数据结构:堆
实现堆排序这里有三种思路:
1. 直接将数组插入到堆中,然后再将堆中的数据插入到数组中。
2. 向上调整算法建堆,然后使用堆删除的思想来排序。
3. 向下调整算法建堆,然后使用堆删除的思想来排序。
1.1直接使用堆进行插入
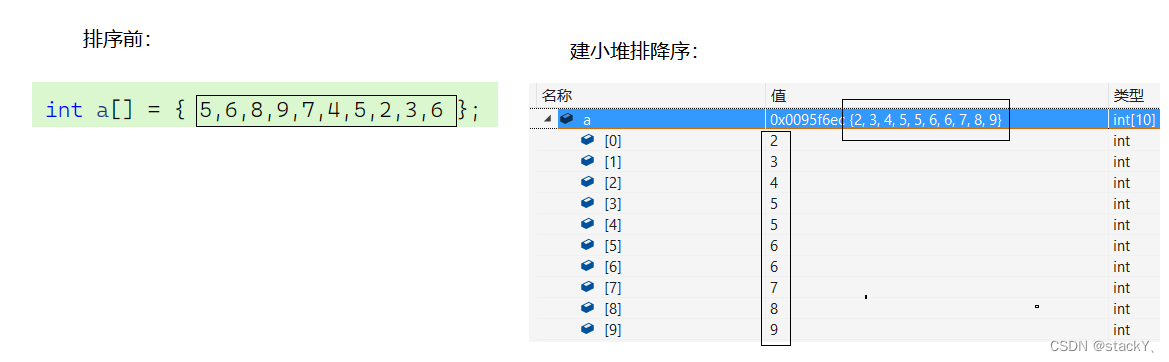
先创建一个堆,然后将数组中的元素依次插入到堆中,如果是大堆在插入完之后就排序成了降序,然后将堆中的数据依次拷贝到数组中,这样子就完成了排序。
代码演示:
// 堆 #include <stdio.h> #include <stdlib.h> #include <assert.h> #include <stdbool.h> //创建堆 //顺序表 typedef int HPDataType; typedef struct Heap { HPDataType* a; int size; //有效元素个数 int capacity; //容量 }Heap; //初始化 void HeapInit(Heap* php); //销毁 void HeapDestroy(Heap* php); //插入 void HeapPush(Heap* php, HPDataType x); //删除 void HeapPop(Heap* php); //判空 bool HeapEmpty(Heap* php); //获取堆顶元素 HPDataType HeapTop(Heap* php); //初始化 void HeapInit(Heap* php) { php->a = NULL; php->size = 0; php->capacity = 0; } //销毁 void HeapDestroy(Heap* php) { free(php->a); php->a = NULL; php->size = php->capacity = 0; } //交换函数 void Swap(HPDataType* p1, HPDataType* p2) { HPDataType tmp = *p1; *p1 = *p2; *p2 = tmp; } //向上调整算法 void AdjustUp(HPDataType* a, int child) { //父节点 int parent = (child - 1) / 2; //向上交换 while (child > 0) { //判断父子大小关系 if (a[child] < a[parent]) { //交换 Swap(&a[child], &a[parent]); //更新父子关系 child = parent; parent = (child - 1) / 2; } else { break; } } } //插入 void HeapPush(Heap* php, HPDataType x) { assert(php); //插入数据的过程 //容量不够则需要扩容 //判断空间是否不足 if (php->size == php->capacity) { int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity; //为堆开辟空间 HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity); if (tmp == NULL) { perror("realloc fail"); return; } php->capacity = newcapacity; php->a = tmp; } //插入数据 php->a[php->size] = x; php->size++; //向上调整 AdjustUp(php->a, php->size - 1); } //向下调整 void AdjustDown(HPDataType* a, int n, int parent) { //假设左孩子为左右孩子中最小的节点 int child = parent * 2 + 1; while (child < n) //当交换到最后一个孩子节点就停止 { if (child + 1 < n //判断是否存在右孩子 && a[child + 1] < a[child]) //判断假设的左孩子是否为最小的孩子 { child++; //若不符合就转化为右孩子 } //判断孩子和父亲的大小关系 if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); //更新父亲和孩子节点 parent = child; child = parent * 2 + 1; } else { break; } } } //删除 void HeapPop(Heap* php) { assert(php); //判断堆是否为空 assert(!HeapEmpty(php)); //交换堆顶的数据和最后的数据 Swap(&php->a[0], &php->a[php->size - 1]); //删除最后的数据 php->size--; //向下调整 AdjustDown(php->a, php->size, 0); } //判空 bool HeapEmpty(Heap* php) { assert(php); return php->size == 0; } //获取堆顶元素 HPDataType HeapTop(Heap* php) { assert(php); //判断堆是否为空 assert(!HeapEmpty(php)); return php->a[0]; } //堆排序 void HeapSort(int* a, int n) { //建堆 Heap hp; HeapInit(&hp); //将数组先插入到堆中实现堆中的大小堆排序 for (int i = 0; i < n; i++) { HeapPush(&hp, a[i]); } //再将堆中的数据拷贝到数组中 int i = 0; while (!HeapEmpty(&hp)) { //保存堆顶元素 int top = HeapTop(&hp); //拷贝 a[i++] = top; HeapPop(&hp); } HeapDestroy(&hp); } int main() { int a[] = { 5,6,8,9,7,4,5,2,3,6 }; int sz = sizeof(a) / sizeof(int); HeapSort(a, sz); return 0; }我们在这里建的是小堆,所以是排成了升序的状态,建大堆只要将向上调整和向下调整的小于号换成大于号即可。
这种算法有点弊端:
1. 必须先要有一个堆,太麻烦。
2. 将数组的数据拷贝至堆,又将堆的数据拷贝至数组,空间复杂度上面代价有点大。
但是这种算法的时间复杂度也是不错的,在前面我们讲堆的时候提到过向上调整算法和向下调整算法,这两种算法的时间复杂度都是O(logN),那么在这个堆排序的算法中的时间复杂度加上遍历数组的时间复杂度合起来为O(N*logN)。
1.2向上调整算法建堆
在使用向上调整算法和向下调整算法的时候如果要达到降序的目的应该建大堆还是小堆?如果要达到升序的目的应该建大堆还是小堆?
我们在这里来思考一下:
按照以往的思路:要排成降序需要建大堆,这样就保证了最大的一个在堆顶,然后将除了堆顶剩下的数据看作一个堆,再找到次大的,这时就面临两个问题:
1. 将剩下的数据看作一个堆时又需要重新建堆,代价有点大。
2. 如果将剩下的数据重新建堆,那么它们原来的父子关系就乱套了,从之前的兄弟变成父子或许有点扯淡。
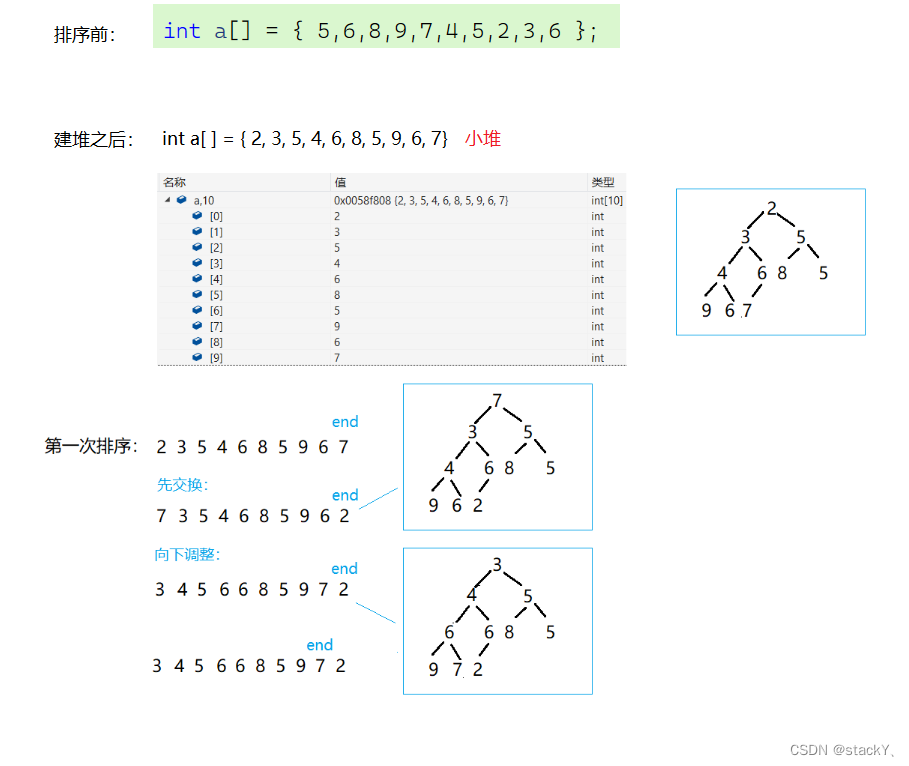
那么我们就来换一种思路,这种思路和删除数据时的思路一样,我们要排成降序我们就建小堆,那么这时堆顶的数据就是最小的,然后将堆顶的数据和最后一个数据交换,这时堆的最后一个数据就是最小的,此时,就不需要将最后一个数据看作堆中的数据,然后再对剩余数据进行向下调整,再找出次小的,再交换至倒数第二个位置......这样子依次类推,直到全部找出来。同样的,要排成升序就建大堆,找出最大的交换,再找次大的,再交换......依次类推同样也可以完成升序。
这里还有需要注意的一个点,我们要从哪里开始进行向上调整建堆?之前说过向上调整算法调整的节点的上面必须是一个堆,因此我们需要从第一个结点开始进行向上调整建堆,因为第一个结点就是一个堆,所以我们将第一个结点看作堆,然后从第二个位置开始插入,前面的结点是堆,符合。
代码演示:
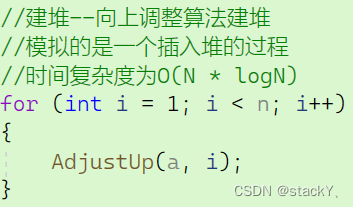
//交换函数 void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } //向上调整算法 void AdjustUp(int* a, int child) { //父节点 int parent = (child - 1) / 2; //向上交换 while (child > 0) { //判断父子大小关系 if (a[child] < a[parent]) { //交换 Swap(&a[child], &a[parent]); //更新父子关系 child = parent; parent = (child - 1) / 2; } else { break; } } } //向下调整 void AdjustDown(int* a, int n, int parent) { //假设左孩子为左右孩子中最小的节点 int child = parent * 2 + 1; while (child < n) //当交换到最后一个孩子节点就停止 { if (child + 1 < n //判断是否存在右孩子 && a[child + 1] < a[child]) //判断假设的左孩子是否为最小的孩子 { child++; //若不符合就转化为右孩子 } //判断孩子和父亲的大小关系 if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); //更新父亲和孩子节点 parent = child; child = parent * 2 + 1; } else { break; } } } void HeapSort(int* a, int n) { //建堆--向上调整算法建堆 //模拟的是一个插入堆的过程 for (int i = 1; i < n; i++) { AdjustUp(a, i); } int end = n - 1; while (end > 0) { //交换堆顶和最后一个数据的位置 Swap(&a[0], &a[end]); //向下调整,找次小的 AdjustDown(a, end, 0); end--; } } int main() { int a[] = { 5,6,8,9,7,4,5,2,3,6 }; int sz = sizeof(a) / sizeof(int); HeapSort(a, sz); return 0; }我们在这里建的是小堆,所以是排成了降序的状态,建大堆只要将向上调整和向下调整的小于号换成大于号即可。
1.3向下调整算法建堆
排降序建小堆,排升序建大堆,当我们使用向上调整算法来建堆实现堆排序时,需要用到向上调整算法和向下调整算法,这个有点太麻烦,那既然在交换数据之后要进行向下调整,那不妨直接使用向下调整算法来直接建堆。
向下调整算法使用的前提是向下调整的结点的下面必须是堆,我们不妨画图来观察一下:
我们知道一个叶子节点本身就是大堆或者小堆,因此我们可以在叶子节点上面下下功夫。
向下调整算法的下面必须是堆:
而叶子节点恰好又是堆,那么叶子节点就可以不用处理,那么我们就可以倒着来进行建堆,从最后一个非叶子节点开始调整(倒数第一个叶子节点的父亲开始调整)。根据孩子与父亲的关系找到父亲然后调整建堆,由于叶子节点本身就是堆,从它的父亲开始调整也符合向下调整算法的逻辑。
代码演示:
//交换函数 void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } //向下调整 void AdjustDown(int* a, int n, int parent) { //假设左孩子为左右孩子中最小的节点 int child = parent * 2 + 1; while (child < n) //当交换到最后一个孩子节点就停止 { if (child + 1 < n //判断是否存在右孩子 && a[child + 1] < a[child]) //判断假设的左孩子是否为最小的孩子 { child++; //若不符合就转化为右孩子 } //判断孩子和父亲的大小关系 if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); //更新父亲和孩子节点 parent = child; child = parent * 2 + 1; } else { break; } } } void HeapSort(int* a, int n) { //建堆--向下调整算法建堆 for (int i = ((n - 1) - 1) / 2; i >= 0; --i) {// 这里的n-1表示最后一个叶子节点 // 最后一个叶子节点的父亲就是: // (n-1)-1 /2; AdjustDown(a, n, i); } int end = n - 1; while (end > 0) { //交换堆顶和最后一个数据的位置 Swap(&a[0], &a[end]); //向下调整,找次小的 AdjustDown(a, end, 0); end--; } } int main() { int a[] = { 5,6,8,9,7,4,5,2,3,6 }; int sz = sizeof(a) / sizeof(int); HeapSort(a, sz); return 0; }
2.算法时间复杂度
一个算法的好与坏取决与它的时间和空间,那么对于向上调整建堆和向下调整建堆哪种方法的时间复杂度更优呢?我们可以一一来计算一下。
2.1向下调整建堆算法时间复杂度
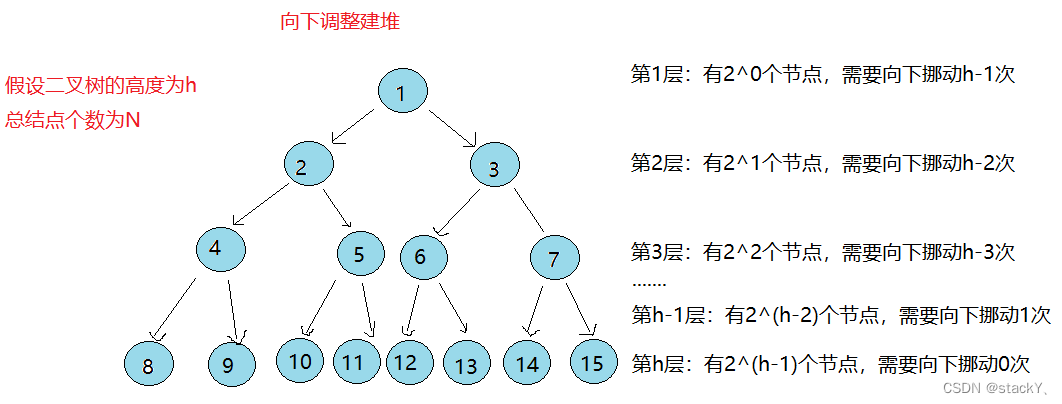
假设二叉树的高度为h,总结点个数为N
第1层: 有2^0个节点,需要向下挪动h-1次
第2层: 有2^1个节点,需要向下挪动h-2次
第3层: 有2^2个节点,需要向下挪动h-3次
......
第h-1层: 有2^(h-2)个节点,需要向下挪动1次
第h层: 有2^(h-1)个节点,需要向下挪动0次总共合计需要挪动:
F(h) = 2^(h-2) * 1 + 2^(h-3) * 2 + ...... + 2^1 * (h-2) + 2^0 * (h-1)
使用错位相减法:
2F(h) = 2^(h-1) * 1 + 2^(h-2) * 2 + 2^(h-3) * 2 + ...... + 2^2 * (h-2) + 2^1 * (h-1)
-
F(h) = 2^(h-2) * 1 + 2^(h-3) * 2 + ...... + 2^1 * (h-2) + 2^0 * (h-1)
F(h) = 2^h - 1 - h
这棵树的中的节点的个数为N = 2^h-1 ==> h = log(N+1)
F(N) = N - log(N+1)
因此向下调整算法的时间复杂度为O(N)
2.2向上调整建堆的时间复杂度
向上调整很明显就是一个多乘多的问题,单单只看最后一层,节点越多,调整的次数越多,那这就完蛋了,向下调整算法最后一层的节点时不需要调整的,那这就很明显了,向下调整算法明显优势于向上调整算法,那么到底能快多少呢?我们一起来计算一下:
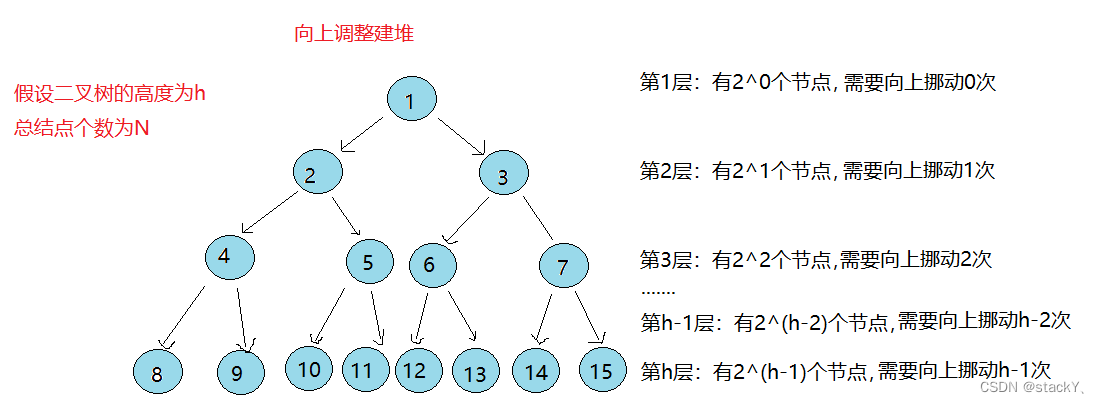
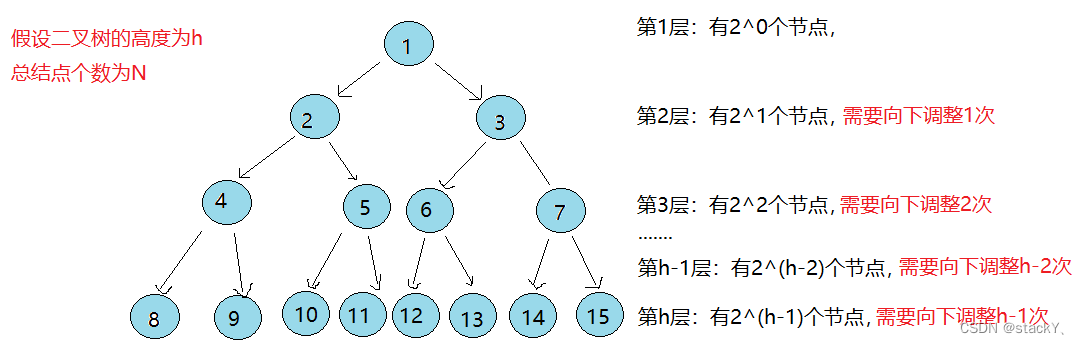
假设二叉树的高度为h,总结点个数为N
第1层: 有2^0个节点,需要向下挪动0次
第2层: 有2^1个节点,需要向下挪动1次
第3层: 有2^2个节点,需要向下挪动2次
......
第h-1层: 有2^(h-2)个节点,需要向下挪动h-2次
第h层: 有2^(h-1)个节点,需要向下挪动h-1次总共合计需要挪动:
F(h) = 2^1 * 1 + 2^2 * 2 + ...... + 2^(h-2) * (h-2) + 2^(h-1) * (h-1)
使用错位相减法:
2F(h) = 2^2 * 1 + 2^3 * 2 + ...... + 2^(h-1) * (h-2) + 2^h * (h-1)
-
F(h) = 2^1 * 1 + 2^2 * 2 + ...... + 2^(h-2) * (h-2) + 2^(h-1) * (h-1)F(h) = 2^1 * 1 + 2^2 * 2 + ...... + 2^(h-2) * (h-2) + 2^(h-1) * (h-1)
= - 2^1 - 2^2 - 2^3 - ...... - 2^(h-2) - 2^(h-1) + 2^h * (h-1)
= - 2^h + 2 - 2^h + 2^h * h
= 2^h * (h-2) + 2
这棵树的中的节点的个数为N = 2^h-1 ==> h = log(N+1)
F(N) = (N + 1) * (log(N + 1) - 2) + 2
因此向上调整算法的时间复杂度为O(N * logN)
3.堆排序的时间复杂度
计算出了向下调整建堆的时间复杂度,我们再来看看堆排序算法的整体的时间复杂度。
这时我们就要计算筛选数据操作时的交换数据和向下调整的时间复杂度:
这里为什么最上面的反而不用向下调整那么多次了,是因为在调整上面的数据时,下面的数据已经是一个堆了,所以筛选数据的过程就和向上调整建堆的时间复杂度一样。
时间复杂度是O(N * logN )
那么再加上向下调整建堆的时间复杂度就是O(N) + O(N * logN)
所以整个堆排序算法的时间复杂度为O(N * logN)
4.完整堆排序代码
//交换函数 void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } //向下调整 void AdjustDown(int* a, int n, int parent) { //假设左孩子为左右孩子中最小的节点 int child = parent * 2 + 1; while (child < n) //当交换到最后一个孩子节点就停止 { if (child + 1 < n //判断是否存在右孩子 && a[child + 1] < a[child]) //判断假设的左孩子是否为最小的孩子 { child++; //若不符合就转化为右孩子 } //判断孩子和父亲的大小关系 if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); //更新父亲和孩子节点 parent = child; child = parent * 2 + 1; } else { break; } } } //O(N * logN) void HeapSort(int* a, int n) { //建堆--向下调整算法建堆 //时间复杂度为O(N) for (int i = ((n - 1) - 1) / 2; i >= 0; --i) {// 这里的n-1表示最后一个叶子节点 // 最后一个叶子节点的父亲就是: // (n-1)-1/2; AdjustDown(a, n, i); } //O(N * logN) int end = n - 1; while (end > 0) { //交换堆顶和最后一个数据的位置 Swap(&a[0], &a[end]); //向下调整,找次小的 AdjustDown(a, end, 0); end--; } } int main() { int a[] = { 5,6,8,9,7,4,5,2,3,6 }; int sz = sizeof(a) / sizeof(int); HeapSort(a, sz); return 0; }
朋友们、伙计们,美好的时光总是短暂的,我们本期的的分享就到此结束,最后看完别忘了留下你们弥足珍贵的三连喔,感谢大家的支持!


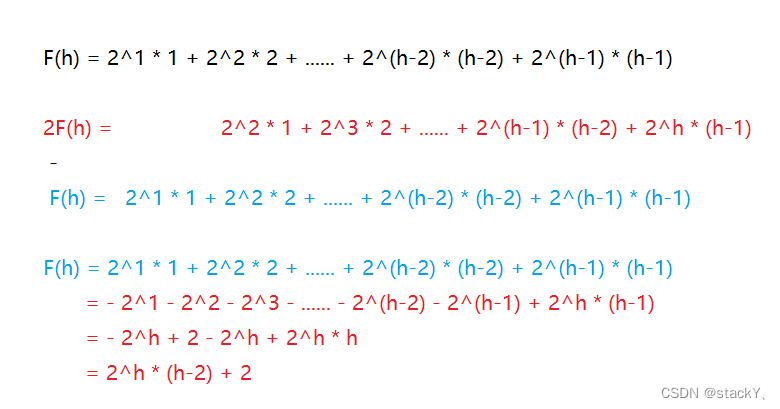






 U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。...
QT多线程的5种用法,通过使用线程解决UI主界面的耗时操作代码,防止界面卡死。... stm32使用HAL库配置串口中断收发数据(保姆级教程)
stm32使用HAL库配置串口中断收发数据(保姆级教程) 分享几个国内免费的ChatGPT镜像网址(亲测有效)
分享几个国内免费的ChatGPT镜像网址(亲测有效) Allegro16.6差分等长设置及走线总结
Allegro16.6差分等长设置及走线总结