您现在的位置是：首页 >技术杂谈 >数据结构之排序专题 —— 快速排序原理以及改进方法（添加随机，三路快排）网站首页技术杂谈
数据结构之排序专题 —— 快速排序原理以及改进方法（添加随机，三路快排）
简介数据结构之排序专题 —— 快速排序原理以及改进方法（添加随机，三路快排）
内容概述
尽管此类博客已经非常非常多，而且也有很多写得很好，但还是想记录一下，用最容易理解的方式，并且多补充了一些例子。
整理云盘的时候发现大一时候的笔记，用的是 txt 文本文件记录的，格式之丑陋可想而知。周六有时间便整理了一下，多少有点怀念那段时光，特记录于此。
快速排序基础核心版
一句话概述：快速排序是一种基于分治策略的排序算法，通过选择一个基准元素将数组分为两个子数组，并递归地对子数组进行排序，最终实现整个数组的排序。
先看例子，再去理解原理
“一句话概述” 中提到选一个基准元素，我们记作 key，接下来的每次排序都会基于 key 而展开，并且根据 key 划分为两个子数组，大于等于 key 的为一组，小于 key 的为一组。
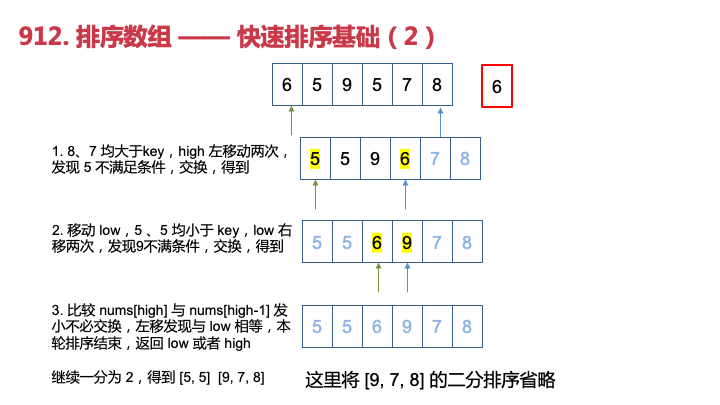
例子1： {3, 5, 1, 6, 2, 9, 5, 7, 8}
开始排序前: 3 5 1 6 2 9 5 7 8
第1次排序 key = 3 排序前 3 5 1 6 2 9 5 7 8 排序后: 2 1 3 6 5 9 5 7 8
第2次排序 key = 2 排序前 2 1 排序后: 1 2
第3次排序 key = 6 排序前 6 5 9 5 7 8 排序后: 5 5 6 9 7 8
第4次排序 key = 5 排序前 5 5 排序后: 5 5
第5次排序 key = 9 排序前 9 7 8 排序后: 8 7 9
第6次排序 key = 8 排序前 8 7 排序后: 7 8
排序完成后: 1 2 3 5 5 6 7 8 9
例子2： {4, 4, 1, 1, 2, 2, 3, 3, 5}
开始排序前: 4 4 1 1 2 2 3 3 5
第1次排序 key = 4 排序前 4 4 1 1 2 2 3 3 5 排序后: 3 4 1 1 2 2 3 4 5
第2次排序 key = 3 排序前 3 4 1 1 2 2 3 排序后: 2 2 1 1 3 4 3
第3次排序 key = 2 排序前 2 2 1 1 排序后: 1 2 1 2
第4次排序 key = 1 排序前 1 2 1 排序后: 1 2 1
第5次排序 key = 2 排序前 2 1 排序后: 1 2
第6次排序 key = 4 排序前 4 3 排序后: 3 4
排序完成后: 1 1 2 2 3 3 4 4 5
例子3： {1, 2, 3, 4, 5, 6, 7, 8, 1}
开始排序前: 1 2 3 4 5 6 7 8 1
第1次排序 key = 1 排序前 1 2 3 4 5 6 7 8 1 排序后: 1 2 3 4 5 6 7 8 1
第2次排序 key = 2 排序前 2 3 4 5 6 7 8 1 排序后: 1 2 4 5 6 7 8 3
第3次排序 key = 4 排序前 4 5 6 7 8 3 排序后: 3 4 6 7 8 5
第4次排序 key = 6 排序前 6 7 8 5 排序后: 5 6 8 7
第5次排序 key = 8 排序前 8 7 排序后: 7 8
排序完成后: 1 1 2 3 4 5 6 7 8
基本原理介绍
一句话概述：快速排序是一种基于分治策略的排序算法，通过选择一个基准元素将数组分为两个子数组，并递归地对子数组进行排序，最终实现整个数组的排序。
代码实现 1 —— 不带打印中间结果
#include <iostream>
#include <algorithm>
#include <cstdlib>
using namespace std;
/**
* 根据 nums[low] 作为参考，将数组划分为两组
* @param nums 原数组
* @param low 需要排序的子数组的索引开始
* @param high 需要排序的子数组的索引结束
* @return low 或者 high 因为二者相等，以后将会根据这个索引将原数组分为两个子数组
*/
int partition(vector<int>& nums, int low, int high) {
int key = nums[low];
while (low < high) {
// 如果 nums[high] 一直大于等于 key，左移
while (low < high && nums[high] >= key) {
high--;
}
// 遇到了不符合条件的，交换
swap(nums[low], nums[high]);
while (low < high && nums[low] <= key) {
low++;
}
swap(nums[low], nums[high]);
}
return low;
}
/**
* 快速排序
* @param nums 待排序的数组
* @param low 待排序的数组的开始索引
* @param high 待排序的数组的结束索引
*/
void quickSort(vector<int>& nums, int low, int high) {
if (low < high) {
int key = partition(nums, low, high);
quickSort(nums, low, key - 1);
quickSort(nums, key + 1, high);
}
}
/**
* 快速排序
* @param nums 待排序的数组
*/
void quickSort(vector<int>& nums) {
quickSort(nums, 0, nums.size() - 1);
}
int main() {
vector<int> nums = {3, 5, 1, 6, 2, 9, 5, 7, 8};
quickSort(nums);
for (auto num : nums) {
cout<<num<<" ";
}
cout<<endl;
return 0;
}
代码实现 2 —— 打印中间结果
#include <iostream>
#include <algorithm>
#include <cstdlib>
using namespace std;
// 用来记录排序的序号
int sortNum = 1;
/**
* 打印数组当前状态
* @param nums 数组
*/
void printNums(vector<int> nums, int low, int high) {
for (int i = low; i <= high; i++) {
cout<<nums[i]<<" ";
}
}
/**
* 根据 nums[low] 作为参考，将数组划分为两组
* @param nums 原数组
* @param low 需要排序的子数组的索引开始
* @param high 需要排序的子数组的索引结束
* @return low 或者 high 因为二者相等，以后将会根据这个索引将原数组分为两个子数组
*/
int partition(vector<int>& nums, int low, int high) {
int start = low, end = high;
int key = nums[low];
cout<<"第"<<sortNum++<<"次排序 key = "<<key<<" 排序前 ";
printNums(nums, start, end);
while (low < high) {
// 如果 nums[high] 一直大于等于 key，左移
while (low < high && nums[high] >= key) {
high--;
}
// 遇到了不符合条件的，交换
swap(nums[low], nums[high]);
while (low < high && nums[low] <= key) {
low++;
}
swap(nums[low], nums[high]);
}
cout<<" 排序后: ";
printNums(nums, start, end);
cout<<endl;
return low;
}
/**
* 快速排序
* @param nums 待排序的数组
* @param low 待排序的数组的开始索引
* @param high 待排序的数组的结束索引
*/
void quickSort(vector<int>& nums, int low, int high) {
if (low < high) {
int key = partition(nums, low, high);
quickSort(nums, low, key - 1);
quickSort(nums, key + 1, high);
}
}
/**
* 快速排序
* @param nums 待排序的数组
*/
void quickSort(vector<int>& nums) {
quickSort(nums, 0, nums.size() - 1);
}
int main() {
vector<int> nums = {3, 5, 1, 6, 2, 9, 5, 7, 8};
cout<<"开始排序前: ";
printNums(nums, 0, nums.size() - 1);
cout<<endl;
quickSort(nums);
cout<<"排序完成后: ";
printNums(nums, 0, nums.size() - 1);
return 0;
}
#include <iostream>
#include <algorithm>
#include <cstdlib>
using namespace std;
// 用来记录排序的序号
int sortNum = 1;
/**
* 打印数组当前状态
* @param nums 数组
*/
void printNums(vector<int> nums) {
for (auto num : nums) {
cout<<num<<" ";
}
}
/**
* 根据 nums[low] 作为参考，将数组划分为两组
* @param nums 原数组
* @param low 需要排序的子数组的索引开始
* @param high 需要排序的子数组的索引结束
* @return low 或者 high 因为二者相等，以后将会根据这个索引将原数组分为两个子数组
*/
int partition(vector<int>& nums, int low, int high) {
int key = nums[low];
while (low < high) {
// 如果 nums[high] 一直大于等于 key，左移
while (low < high && nums[high] >= key) {
high--;
}
// 遇到了不符合条件的，交换
swap(nums[high], nums[low]);
while (low < high && nums[low] <= key) {
low++;
}
swap(nums[low], nums[high]);
}
cout<<"第"<<sortNum++<<"次排序后: ";
printNums(nums);
cout<<" 本次排序的key为"<<key<<endl;
return low;
}
/**
* 快速排序
* @param nums 待排序的数组
* @param low 待排序的数组的开始索引
* @param high 待排序的数组的结束索引
*/
void quickSort(vector<int>& nums, int low, int high) {
if (low < high) {
int key = partition(nums, low, high);
quickSort(nums, low, key - 1);
quickSort(nums, key + 1, high);
}
}
/**
* 快速排序
* @param nums 待排序的数组
*/
void quickSort(vector<int>& nums) {
quickSort(nums, 0, nums.size() - 1);
}
int main() {
vector<int> nums = {3, 5, 1, 6, 2, 9, 5, 7, 8};
cout<<"开始排序前: ";
printNums(nums);
cout<<endl;
quickSort(nums);
return 0;
}
最终输出结果为：
开始排序前: 3 5 1 6 2 9 5 7 8
第1次排序 key = 3 排序前 3 5 1 6 2 9 5 7 8 排序后: 2 1 3 6 5 9 5 7 8
第2次排序 key = 2 排序前 2 1 排序后: 1 2
第3次排序 key = 6 排序前 6 5 9 5 7 8 排序后: 5 5 6 9 7 8
第4次排序 key = 5 排序前 5 5 排序后: 5 5
第5次排序 key = 9 排序前 9 7 8 排序后: 8 7 9
第6次排序 key = 8 排序前 8 7 排序后: 7 8
排序完成后: 1 2 3 5 5 6 7 8 9
添加随机选择 key
因为每次排序从待排序的数组中 low 选取很有可能影响性能，可能出现每次都选择数组中的 “第二大值” 或 “第二小值” 等等，而我们期望的是每次都能选中间值，分而治之的效率才最高。
这里我们添加随机选择 key 的方法来达到这个目的。就是在之前的基础上增加两行代码如下
int index = rand() % (high - low) + low;
swap(nums[index], nums[low]);
全部代码如下：
#include <iostream>
#include <algorithm>
#include <cstdlib>
using namespace std;
/**
* 根据 nums[low] 作为参考，将数组划分为两组
* @param nums 原数组
* @param low 需要排序的子数组的索引开始
* @param high 需要排序的子数组的索引结束
* @return low 或者 high 因为二者相等，以后将会根据这个索引将原数组分为两个子数组
*/
int partition(vector<int>& nums, int low, int high) {
int index = rand() % (high - low) + low;
swap(nums[index], nums[low]);
int key = nums[low];
while (low < high) {
// 如果 nums[high] 一直大于等于 key，左移
while (low < high && nums[high] >= key) {
high--;
}
// 遇到了不符合条件的，交换
swap(nums[low], nums[high]);
while (low < high && nums[low] <= key) {
low++;
}
swap(nums[low], nums[high]);
}
return low;
}
/**
* 快速排序
* @param nums 待排序的数组
* @param low 待排序的数组的开始索引
* @param high 待排序的数组的结束索引
*/
void quickSort(vector<int>& nums, int low, int high) {
if (low < high) {
int key = partition(nums, low, high);
quickSort(nums, low, key - 1);
quickSort(nums, key + 1, high);
}
}
/**
* 快速排序
* @param nums 待排序的数组
*/
void quickSort(vector<int>& nums) {
quickSort(nums, 0, nums.size() - 1);
}
int main() {
vector<int> nums = {3, 5, 1, 6, 2, 9, 5, 7, 8};
quickSort(nums);
for (auto num : nums) {
cout<<num<<" ";
}
cout<<endl;
return 0;
}
三路快排
三路快排其实也很简单，前面提到的快排每次排序根据 key 将数组划分为 大于等于 key 的和小于 key 的，三路快排的思路就是将 等于 key 的单独处理一下，不再和前面提到的合到了 “大于等于” 这一类中。
那如何实现这个效果呢 ？
基本思路为：除了 low 与 high，添加第3个指针 mid，mid 与 low 同时出发一起去寻找 high，并且 mid 走得更快 —— nums[low] < key 时二者都走，nums[low] == key 时只有 mid 往前走，当 mid 找到 high 时停止本次循环。
这个地方不做PPT详细描述了，跟前面的方法基本是一致的，改进的地方即前面提到的 “基本思路”。
#include <iostream>
#include <algorithm>
#include <cstdlib>
using namespace std;
/**
* 根据 nums[low] 作为参考，将数组划分为两组
* @param nums 原数组
* @param low 需要排序的子数组的索引开始
* @param high 需要排序的子数组的索引结束
* @return low 或者 high 因为二者相等，以后将会根据这个索引将原数组分为两个子数组
*/
pair<int,int> partition(vector<int>& nums, int low, int high) {
int index = rand() % (high - low) + low;
swap(nums[index], nums[low]);
// 作为比较的对象，接下根据大小关系把数组分为三类
int key = nums[low];
// 记录一下开始的位置，最后需要用到
int start = low;
// mid 指针走的比 low 快，会更快找到 high 然后停止
int mid = low + 1;
// 注意这里的停止条件是 mid 找到 high
while (mid <= high) {
// 如果 nums[mid] 小于 key，就放到左边 的 low + 1 的位置
if (nums[mid] < key) {
swap(nums[++low], nums[mid++]);
} else if (nums[mid] > key) {
// 如果大于 key 的话这里和两路排序没有区别，但是之前的low换成了现在的mid，注意mid指针不需要移动
swap(nums[mid], nums[high--]);
} else {
// 如果相等的话，那么只需要移动mid指针，因为其他的两端已经基本有序，本地的移动跟它们没有关系
mid++;
}
}
// 最后一定要把最开始选择的 key 移动中间去，换完成后
swap(nums[start], nums[low]);
return {low, high};
}
/**
* 快速排序
* @param nums 待排序的数组
* @param low 待排序的数组的开始索引
* @param high 待排序的数组的结束索引
*/
void quickSort(vector<int>& nums, int low, int high) {
if (low < high) {
pair<int, int> part = partition(nums, low, high);
quickSort(nums, low, part.first - 1);
quickSort(nums, part.second + 1, high);
}
}
/**
* 快速排序
* @param nums 待排序的数组
*/
void quickSort(vector<int>& nums) {
quickSort(nums, 0, nums.size() - 1);
}
int main() {
vector<int> nums = {3, 5, 1, 6, 2, 9, 5, 7, 8};
quickSort(nums);
for (auto num : nums) {
cout<<num<<" ";
}
cout<<endl;
return 0;
}
这里补充几个例子：
例子1：{5, 1, 5, 6, 5, 9, 5, 7, 8}
本例子比较特殊，因为第一个元素就是我们期望的，也就是数组中出现次数最多的，本次排序只需要4次。如果我们将前两个元素的位置调换，结果就有些不一样了（参看例子2）。
开始排序前: 5 1 5 6 5 9 5 7 8
第1次排序： 1 5 5 5 5 9 7 8 6 key = 5 low = 1 high=4
第2次排序： 6 7 8 9 key = 9 low = 8 high=8
第3次排序： 6 8 7 key = 6 low = 5 high=5
第4次排序： 7 8 key = 8 low = 7 high=7
排序完成后: 1 5 5 5 5 6 7 8 9
例子2：{1, 5, 5, 6, 5, 9, 5, 7, 8};
由于第一个key不是出现次数最多的5，所以第一次排序后只是单纯地确定了 1 的位置。
开始排序前: 1 5 5 6 5 9 5 7 8
第1次排序： 1 5 6 5 9 5 7 8 5 key = 1 low = 0 high=0
第2次排序： 5 5 5 5 7 8 9 6 key = 5 low = 1 high=4
第3次排序： 6 7 9 8 key = 7 low = 6 high=6
第4次排序： 8 9 key = 9 low = 8 high=8
排序完成后: 1 5 5 5 5 6 7 8 9
例子3：{7, 5, 5, 6, 5, 9, 5, 7, 8}
这个例子不同之处在于出现重复的不只是 5 了，还有 7 也重复过两次，所以排序更快（3次）。
开始排序前: 7 5 5 6 5 9 5 7 8
第1次排序： 5 5 5 6 5 7 7 8 9 key = 7 low = 5 high=6
第2次排序： 5 5 5 5 6 key = 5 low = 0 high=3
第3次排序： 8 9 key = 8 low = 7 high=7
排序完成后: 5 5 5 5 6 7 7 8 9
例子4：{7, 5, 5, 5, 5, 5, 5, 5, 5}
开始排序前: 7 5 5 5 5 5 5 5 5
第1次排序： 5 5 5 5 5 5 5 5 7 key = 7 low = 8 high=8
第2次排序： 5 5 5 5 5 5 5 5 key = 5 low = 0 high=7
排序完成后: 5 5 5 5 5 5 5 5 7
例子5：{5, 7, 5, 5, 5, 5, 5, 5, 5}
开始排序前: 5 7 5 5 5 5 5 5 5
第1次排序： 5 5 5 5 5 5 5 5 7 key = 5 low = 0 high=7
排序完成后: 5 5 5 5 5 5 5 5 7
例子6：{5, 5, 5, 5, 5, 5, 5, 5, 5}
开始排序前: 5 5 5 5 5 5 5 5 5
第1次排序： 5 5 5 5 5 5 5 5 5 key = 5 low = 0 high=8
排序完成后: 5 5 5 5 5 5 5 5 5
例子6：{3, 1, 2, 4, 2, 2, 2, 1, 5}
开始排序前: 3 1 2 4 2 2 2 1 5
第1次排序： 2 1 2 1 2 2 3 5 4 key = 3 low = 6 high=6
第2次排序： 1 1 2 2 2 2 key = 2 low = 2 high=5
第3次排序： 1 1 key = 1 low = 0 high=1
第4次排序： 4 5 key = 5 low = 8 high=8
排序完成后: 1 1 2 2 2 2 3 4 5
总结
回想一下当初学习排序算法的时候，最头疼的地方应该在于那段 “似懂非懂” 的状态，能够看懂例子，大致能够明白基本原理，但是别说写源码实现算法，就连读懂源码都比较困难，因为很多源码注释太少了，看起来很舒服但对初学者非常不友好。
所以这里决定放弃代码的美观而决定写很多注释的方式，记录一下当初遇到的困难。并且给出例子，记录每次排序的基本过程。因为快排分而治之的思想理解容易但应用起来却不那么直观了，所以可以考虑把各个过程打印出来，给自己分析，也方便别人理解。
历史是个轮回不一定成立，但学习应该是这样的。古人诚不欺我，温故而知新。
Smileyan
2023.05.27 23:41
风语者！平时喜欢研究各种技术，目前在从事后端开发工作，热爱生活、热爱工作。
站长推荐
- stm32使用HAL库配置串口中断收发数据（保姆级教程）
stm32使用HAL库配置串口中断收发数据（保姆级教程） - SpringSecurity实现前后端分离认证授权
SpringSecurity实现前后端分离认证授权 - U8W/U8W-Mini使用与常见问题解决
U8W/U8W-Mini使用与常见问题解决 - 【社区图书馆】伴我前行的一本书《The C Programming Language》
【社区图书馆】伴我前行的一本书《The C Programming Language》 - 【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述
【云原生进阶之容器】第六章容器网络6.6.1--Cilium网络方案概述