数据结构与算法·第2章【线性表】网站首页 技术杂谈

数据结构与算法·第2章【线性表】

call me by ur name 2024-06-30 18:01:02

简介数据结构与算法·第2章【线性表】

线性结构具有以下基本特征：

有唯一的一个被称为首元素（或头元素）的元素，没有直接前驱；有唯一的一个被称为尾元素（或尾节点）的元素，没有直接后继。

数据元素之间存在一对一的线性关系，即除首末元素外，每一个数据元素均只有一个直接前驱和一个直接后继。

线性结构的各个数据元素在逻辑上是线性排列的，即所有数据元素都排列在一条线段上，故称为线性结构。

线性表是以下数据结构的总称

顺序表（SqList）

非循环链表尾结点的指针域保持为NULL

基本操作

在这里插入图片描述
大概看看即可
其中ListInsert(&L,i,e)是插入到 $i$ 之前的位置
第一个元素的位置是i=1，最后一个元素的位置是L.length

结构体定义

在这里插入图片描述

其中，listsize是容量SqList总共能装多少个元素，length是有多少个元素

部分算法的具体实现

初始化
在这里插入图片描述

在这里插入图片描述

插入主要注意超限后，需要realloc

在这里插入图片描述

合并两条顺序表

链表（LinkList）

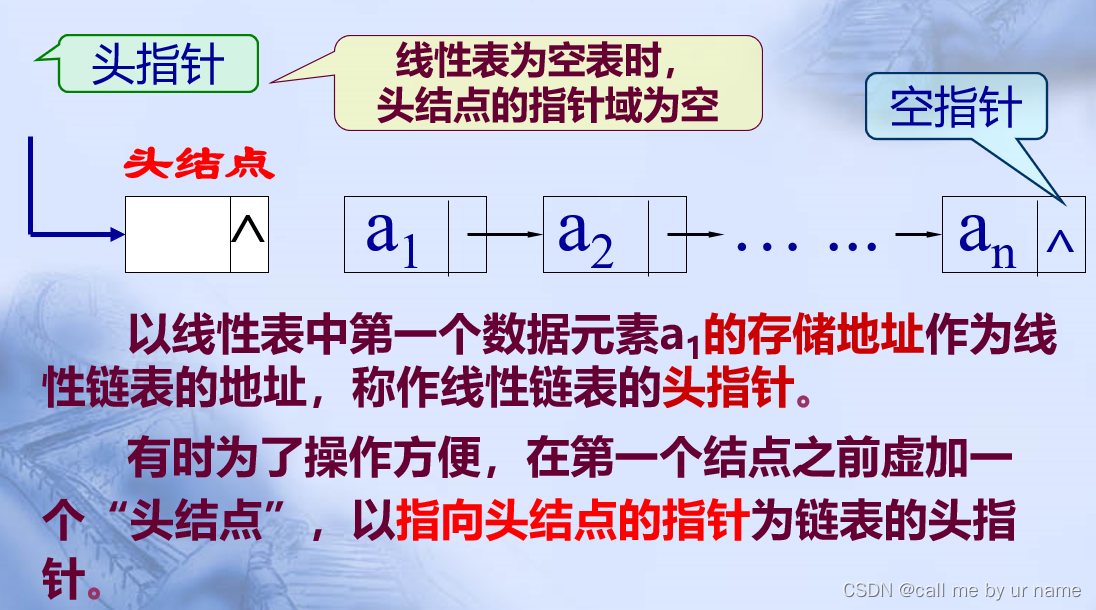
在这里插入图片描述
还是建议带上头结点头指针指向头结点
优点：

链表第一个元素不用特殊处理
空表不用特殊处理

结构体定义

typedef struct  LNode {
      ElemType      data;  // 数据域
      struct LNode   *next;  // 指针域
} LNode, *LinkList;  
LNode *head;     // 定义一个头结点指针
LinkList L = head;   // 定义一个链表L并将头结点指针赋给它

部分算法的具体实现

Status ListDelete_L(LinkList L, int i, ElemType &e) {
p = L;    j = 0;
while (p->next && j < i-1) {  p = p->next;   ++j; } // 寻找第 i 个结点，并令 p 指向其前趋
if  (!(p->next) || j > i-1) 
    return ERROR;  // 删除位置不合理
q = p->next;   p->next = q->next;  // 删除并释放结点
e = q->data;   free(q);
return OK;
}

注意 $p - > n e x t$ 为待删除元素，因为循环条件是 $j < i - 1$

void CreateList_L(LinkList &L, int n) {
    // 逆序输入 n 个数据元素，建立带头结点的单链表
L = (LinkList) malloc (sizeof (LNode));
L->next = NULL;    // 先建立一个带头结点的单链表
for (i = n; i > 0; --i) {
  p = (LinkList) malloc (sizeof (LNode));//生成新结点
  scanf(&p->data);    // 输入元素值
    p->next = L->next; L->next = p; // 插入到表头
}
}

逆序插入早插的在后面
$p - > n e x t = L - > n e x t$

LinkList  CreateList_tail()
{  //用尾插法创建单链表，返回单链表的头指针
   char ch;
   LinkList head,r;// 头指针和尾指针
   ListNode *s;//工作指针
   head=(LinkList)malloc(sizeof(ListNode));//生成头结点
   head->next=NULL;
   r=head;//空表时尾指针也指向头结点
   ch=getchar();//读入第1个字符
   while(ch!='$')
   {  
       s=( ListNode*)malloc(sizeof(ListNode));//生成新结点
       s->data=ch;
       r->next=s;
       r=s;
       ch=getchar();
   }
    r->next=NULL;
    return head;
}

尾指针插入

双向链表

循环链表——尾结点的后继指向头结点注意是头结点
对于双向链表来说：头节点的前驱指向尾结点，尾结点的后继指向头结点

结构体定义

typedef struct  DuLNode {
    ElemType         data;   // 数据域
    struct DuLNode   *prior;  // 指向前驱的指针域
    struct DuLNode  *next;  // 指向后继的指针域
} DuLNode, *DuLinkList;

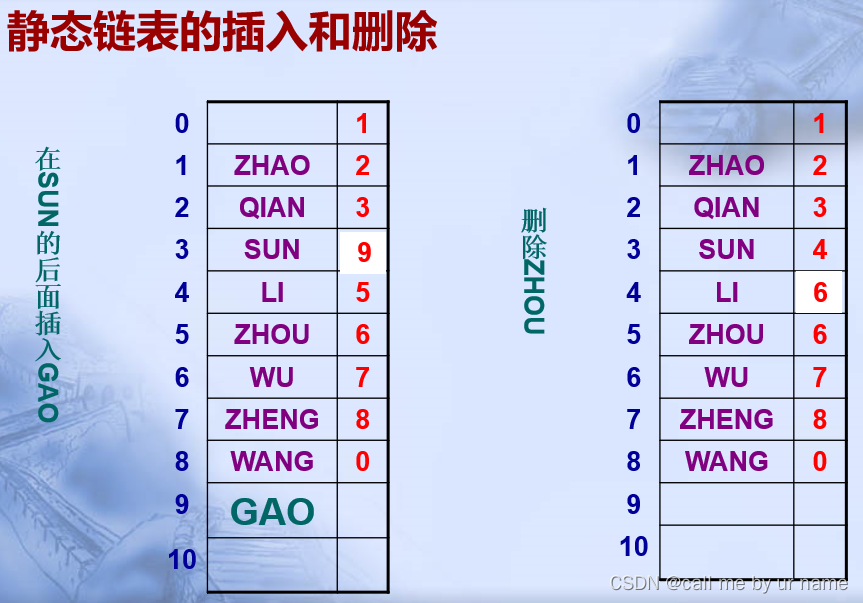
静态链表

#define MAXSIZE   1000  //链表的最大长度
typedef struct {
    ElemType    data;
    int    cur;
}component, SLinkList [ MAXSIZE ];

分别是存储节点数据的 $d a t a$ 和存储下一个节点在数组中下标的 $c u r$ 最后一个元素的cur为0，即最后一个元素的下一个结点是头结点

部分算法

int LocateElem_ SL ( SLinkList S, ElemType e )   {
     //在静态单链线性表L中查找第1个值为e的元素。若找到，则返回它在L中的位序，否则返回0。
     i=S[0].cur;      //i指示表中第一个结点
     while ( i && S[i].data!=e ) i = S[i].cur; //在表中顺链查找
     return i;
} // LocateElem_ SL

在这里插入图片描述

多项式

typedef struct {      // 项的表示
    float  coef;          // 系数
    int   expn;           // 指数
} term, ElemType;

基本操作

在这里插入图片描述

具体实现

void AddPolyn (polynomial &Pa, polynomial &Pb) {
   ha = GetHead (Pa); hb = GetHead (Pb);  //ha和hb分别指向Pa和Pb的头结点
   qa = NextPos ( Pa, ha);  qb = NextPos ( Pb, hb); //pa和pb分别指向La和Lb中当前结点
   while ( qa && qb ){   // La和Lb均非空  
      a = GetCurElem ( qa ); b = GetCurElem ( qb );  //a和b为两表中当前比较元素
      switch (*cmp(a, b)) { 
      case -1: {       // 多项式PA中当前结点的指数值小     
         ha=qa; qa = NextPos ( Pa, qa); break; 
      case 0: {                            // 两者的指数值相等
        sum= a.coef + b.coef ;
        if ( sum != 0.0 ) {  //修改多项式PA中当前结点的系数值
            SetCurElem (qa, sum); ha=qa;}
        else { DelFirst (ha, qa);    FreeNode (qa);}//删除多项式PA中当前结点
            DelFirst(hb, qb); FreeNode(qb);  
            qb=NextPos( Pb, hb); qa = NextPos ( Pa, ha);  
            break;
       case 1: { //多项式PB中当前结点的指数值小
             DelFirst (hb, qb); InsFirst (ha, qb);
             qb =NextPos ( Pb, qb); 
             ha = NextPos ( Pa, qa);   break; 
         }
     }
     if (!ListEmpty (Pb))  Append (Pa, qb);//链接Pb中剩余结点
     FreeNode (hb);      // 释放Pb的头结点
} // AddPolyn