您现在的位置是：首页 >其他 >LeetCode刷题（ACM模式）-02链表网站首页其他

参考引用：代码随想录

• 注：每道 LeetCode 题目都使用 ACM 代码模式，可直接在本地运行，蓝色字体为题目超链接

0. 链表理论基础

0.1 链表定义

• 链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成：一个是数据域，一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向 NULL（空指针）

• 链表的入口节点称为链表的头结点也就是 head

0.2 链表类型

• 单链表

  • 上述说的就是单链表

• 双链表

  • 单链表中的指针域只能指向节点的下一个节点，而双链表的每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点，双链表既可以向前查询也可以向后查询

• 循环链表
  • 循环链表，顾名思义，就是链表首尾相连，循环链表可以用来解决约瑟夫环问题

0.3 链表的存储方式

• 数组是在内存中是连续分布的，但是链表在内存中可不是连续分布的。链表是通过指针域的指针链接在内存中各个节点。所以链表中的节点在内存中不是连续分布的，而是散乱分布在内存中的某地址上，分配机制取决于操作系统的内存管理

• 下图中这个链表起始节点为 2， 终止节点为 7， 各个节点分布在内存的不同地址空间上，通过指针串联在一起

0.4 链表节点定义

• C/C++ 的定义链表节点方式

  // 单链表
  struct ListNode {
      int val; // 节点上存储的元素
      ListNode *next; // 指向下一个节点的指针
      ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
  };
  

• 不定义构造函数也可以，C++ 默认生成一个构造函数，但这个构造函数不会初始化任何成员变量

  // 通过自己定义构造函数初始化节点
  ListNode *head = new ListNode(5);
  

  // 使用默认构造函数初始化节点
  ListNode *head = new ListNode();
  head->val = 5;
  

综上：如果不定义构造函数而使用默认构造函数的话，在初始化的时候就不能直接给变量赋值！

0.5 链表的操作

• 删除节点
  • 删除 D 节点，如图所示：只要将 C 节点的 next 指针指向 E 节点就可以了

D 节点此时依然存留在内存里，只不过没有在这个链表里，在 C++ 最好再手动释放这个 D 节点所占内存

• 添加节点
  • 可以看出链表的增添和删除都是 O(1) 操作，也不会影响到其他节点。但是要注意，如果要删除第 5 个节点，需要从头节点查找到第 4 个节点并通过 next 指针进行删除操作，查找的时间复杂度是 O(n)
    

0.6 数组和链表对比

• 数组在定义的时候，长度就是固定的，如果想改动数组的长度，就需要重新定义一个新的数组
• 链表的长度可以是不固定的，并且可以动态增删，适合数据量不固定，频繁增删，较少查询的场景
  

1. 移除链表元素

203. 移除链表元素
给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回新的头节点

• 示例 1
  
  输入：head = [1,2,6,3,4,5,6], val = 6 输出：[1,2,3,4,5]
• 示例 2
  输入：head = [], val = 1 输出：[]
• 示例 3
  输入：head = [7,7,7,7], val = 7 输出：[]
• 提示
  列表中的节点数目在范围 $[0,10^4]$ 内
  1 <= Node.val <= 50
  0 <= val <= 50

1.1 思路

• 以链表 1 4 2 4 来举例，移除元素 4

• 如果使用 C/C++ 还要从内存中删除这两个移除的节点，清理节点内存之后如图

• 这种情况下的移除操作，就是让节点 next 指针直接指向下一个节点就可以了，那么因为单链表的特殊性，只能指向下一个节点，刚刚删除的是链表的中第二个和第四个节点，那么如果删除的是头结点又该怎么办呢？

链表操作的两种方式

• 1、直接使用原来的链表来进行删除操作
  

  • 移除头结点和移除其他节点的操作是不一样的，因为链表的其他节点都是通过前一个节点来移除当前节点，而头结点没有前一个节点。所以头结点如何移除呢？其实只要将头结点向后移动一位就可以，这样就从链表中移除了一个头结点
    

  • 并将原头结点从内存中删掉
    

在单链表中移除头结点和移除其他节点的操作方式是不一样，并且在写代码的时候需要单独写一段逻辑来处理移除头结点的情况，该如何避免这个问题呢？第二个方法可以实现统一方法移除链表节点

• 代码实现

// 时间复杂度: O(n)
// 空间复杂度: O(1)
#include <iostream>

using namespace std;

struct ListNode {
    int val; // 节点上存储的元素
    ListNode *next; // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
};

class Solution {
public:
    ListNode *removeElements(ListNode *head, int val) {
        // 删除头结点
        while (head != NULL && head->val == val) { // 注意这里不是if
            ListNode *tmp = head; // 用临时指针变量 tmp 记录要删除的头节点
            head = head->next; // 将头结点指针 head 向后移一位，指向下一个节点
            delete tmp; // 使用 delete 语句释放 tmp 指向的内存空间
        }

        // 删除非头结点
        // 定义一个指针变量 cur，初始化为链表头节点 head，表示当前所在节点
        ListNode *cur = head;
        // 遍历链表中从第二个节点开始的所有节点，直到链表末尾或者当前节点的下一个节点为空为止
        while (cur != NULL && cur->next != NULL) {
            if (cur->next->val == val) {
                ListNode *tmp = cur->next; // 用临时指针变量 tmp 记录要删除的下一个节点
                cur->next = cur->next->next; // 将当前节点的 next 指针指向下一个节点的 next 指针，即跳过了要删除的下一个节点
                delete tmp; // 使用 delete 语句释放 tmp 指向的内存空间
            } else { // 如果当前节点的下一个节点的值不等于 val，则将当前节点指针 cur 移动到下一个节点，继续遍历
                cur = cur->next;
            }
        }
        return head;
    }
};

int main(int argc, char *argv[]) {
    ListNode *head = new ListNode(1);
    head->next = new ListNode(2);
    head->next->next = new ListNode(6);
    head->next->next->next = new ListNode(3);
    head->next->next->next->next = new ListNode(4);
    head->next->next->next->next->next = new ListNode(5);
    head->next->next->next->next->next->next = new ListNode(6);

    Solution solution;
    int val = 6;
    // 返回一个指向新链表头节点的指针变量 res
    ListNode *res = solution.removeElements(head, val);

    // 指针变量 res 被不断更新，以指向链表中的每个节点，从而实现对链表的遍历
    while (res != NULL) {
        cout << res->val << "->";
        res = res->next; // 将 res 指向下一个节点
    }
    cout << "NULL" << endl;

    return 0;
}

• 2、设置一个虚拟头结点再进行删除操作
  

  • 这里来给链表添加一个虚拟头结点为新的头结点，此时要移除这个旧头结点元素 1。这样是不是就可以使用和移除链表其他节点的方式统一了呢？来看一下，如何移除元素 1 呢，还是熟悉的方式，然后从内存中删除元素 1。最后在题目中，return 头结点的时候，别忘了 return dummyNode->next;，这才是新的头结点

• 代码实现

// 时间复杂度: O(n)
// 空间复杂度: O(1)
#include <iostream>
using namespace std;

struct ListNode {
    int val; // 节点上存储的元素
    ListNode *next; // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
};

class Solution {
public:
    ListNode *removeElements(ListNode *head, int val) {
        ListNode *dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向 head，这样方便后面做删除操作
        ListNode *cur = dummyHead; // 创建 cur 指针指向虚拟头结点
        while (cur->next != NULL) {
            if (cur->next->val == val) {
                ListNode *tmp = cur->next;
                cur->next = cur->next->next; // 将当前节点指向下一个节点
                delete tmp;
            } else {
                cur = cur->next; // 将当前节点指向下一个节点
            }
        }
        head = dummyHead->next; // 更新链表头部指针为虚拟头结点指向的下一个节点
        delete dummyHead; // 释放虚拟头结点的内存空间
        return head;
    }
};

int main(int argc, char *argv[]) {
    ListNode *head = new ListNode(1);
    head->next = new ListNode(2);
    head->next->next = new ListNode(6);
    head->next->next->next = new ListNode(3);
    head->next->next->next->next = new ListNode(4);
    head->next->next->next->next->next = new ListNode(5);
    head->next->next->next->next->next->next = new ListNode(6);

    Solution solution;
    int val = 6;
    // 返回一个指向新链表头节点的指针变量 res
    ListNode *res = solution.removeElements(head, val);

    // 指针变量 res 被不断更新，以指向链表中的每个节点，从而实现对链表的遍历
    while (res != NULL) {
        cout << res->val << "->";
        res = res->next; // 将 res 指向下一个节点
    }
    cout << "NULL" << endl;

    return 0;
}

2. 设计链表

707. 设计链表
你可以选择使用单链表或者双链表，设计并实现自己的链表

• 单链表中的节点应该具备两个属性：val 和 next 。val 是当前节点的值，next 是指向下一个节点的指针/引用
• 如果是双向链表，则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始

实现 MyLinkedList 类

• MyLinkedList() 初始化 MyLinkedList 对象
• int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1
• void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后，新节点会成为链表的第一个节点
• void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素
• void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将不会插入到链表中
• void deleteAtIndex(int index) 如果下标有效，则删除链表中下标为 index 的节点

• 示例 1
  输入
  [“MyLinkedList”, “addAtHead”, “addAtTail”, “addAtIndex”, “get”, “deleteAtIndex”, “get”]
  [[], [1], [3], [1, 2], [1], [1], [1]]
  输出
  [null, null, null, null, 2, null, 3]
  解释
  MyLinkedList myLinkedList = new MyLinkedList();
  myLinkedList.addAtHead(1);
  myLinkedList.addAtTail(3);
  myLinkedList.addAtIndex(1, 2); // 链表变为 1->2->3
  myLinkedList.get(1); // 返回 2
  myLinkedList.deleteAtIndex(1); // 现在，链表变为 1->3
  myLinkedList.get(1); // 返回 3

• 提示
  0 <= index, val <= 1000
  请不要使用内置的 LinkedList 库
  调用 get、addAtHead、addAtTail、addAtIndex 和 deleteAtIndex 的次数不超过 2000

2.1 思路

• 删除链表节点
  

• 添加链表节点
  

• 设计链表的五个接口

  • 获取链表第 index 个节点的数值
  • 在链表的最前面插入一个节点
  • 在链表的最后面插入一个节点
  • 在链表第 index 个节点前面插入一个节点
  • 删除链表的第 index 个节点

2.2 代码实现

• 设置一个虚拟头结点方式实现

// 时间复杂度: 涉及 index 的相关操作为 O(index), 其余为 O(1)
// 空间复杂度: O(n)
#include <iostream>
using namespace std;

class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode{
        int val;
        LinkedNode *next;
        LinkedNode(int val) : val(val), next(nullptr) {}
    };

    // 初始化链表
    MyLinkedList() {
        _dummyHead = new LinkedNode(0); // 定义一个虚拟头结点
        _size = 0;
    }

    // 获取到第 index 个节点数值，如果 index 是非法数值直接返回 -1
        // 注意：index 是从 0 开始的，第 0 个节点就是头结点
    int get(int index) {
        if (index > (_size - 1) || index < 0) {
            return -1;
        }
        LinkedNode *cur = _dummyHead->next;
        while (index--) {
            cur = cur->next;
        }
        return cur->val;
    }

    // 在链表最前面插入一个节点，插入完成后，新插入的节点为链表新的头结点
    void addAtHead(int val) {
        // 创建一个新的 LinkedNode 对象，使用传递给函数的 val 值进行初始化
            // 这个新节点就是要插入到链表头部的节点
        LinkedNode *newNode = new LinkedNode(val);
        // 指定新节点的 next 指针，将其指向原来的头结点，在新节点和链表中原头节点之间建立链接关系
        newNode->next = _dummyHead->next;
        // 将 _dummyHead->next 的值设置为新节点，这样新节点就成为了链表的新头节点
        _dummyHead->next = newNode; 
        _size++; // 增加链表长度 _size，以跟踪链表中节点的数量
    }

    // 在链表最后面添加一个节点
    void addAtTail(int val) {
        LinkedNode *newNode = new LinkedNode(val);
        LinkedNode *cur = _dummyHead;
        // 通过 while 循环找到链表的最后一个节点，并将其赋值给 cur
        while (cur->next != nullptr) {
            cur = cur->next;
        }
        // 将新节点添加到链表的末尾（即 cur 节点的下一个位置）
        cur->next = newNode;
        _size++;
    }

    // 在第 index 个节点之前插入一个新节点，例如 index 为 0，那么新插入的节点为链表的新头节点
    // 如果 index 等于链表的长度，则说明是新插入的节点为链表的尾结点
    // 如果 index 大于链表的长度，则返回空
    // 如果 index 小于 0，则在头部插入节点
    void addAtIndex(int index, int val) {
        if (index > _size) return;
        if (index < 0) index = 0; // 索引小于 0，则将其设置为 0，以确保新节点插入到链表开头
        LinkedNode *newNode = new LinkedNode(val); // 将要插入的值 val 作为参数传递给构造函数
        LinkedNode *cur = _dummyHead;
        // 使用一个指针 cur 来遍历链表，找到要插入新节点的位置，并将其赋值给 cur
        while (index--) {
            cur = cur->next;
        }
        // 见添加链表节点图示
        newNode->next = cur->next;
        cur->next = newNode;
        _size++;
    }

    // 删除第 index 个节点，如果 index 大于等于链表的长度
        // 直接 return，注意 index 是从 0 开始的
    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode *cur = _dummyHead;
        // 使用一个指针 cur 来遍历链表，找到要删除的节点位置，并将其赋值给 cur
        while (index--) {
            cur = cur->next;
        }
        LinkedNode *tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp; 
        // delete 命令指示释放了 tmp 指针原本所指的那部分内存
        // 被 delete 后的指针 tmp 的值（地址）并非就是 NULL，而是随机值
        // 也就是被 delete 后，如果不加上下面这句，则 tmp 会成为乱指的野指针
        // 如果之后的程序不小心使用了 tmp，会指向难以预想的内存空间
        tmp = nullptr;
        _size--;
    }

    // 打印链表
    void printLinkedList() {
        LinkedNode *cur = _dummyHead;
        while (cur->next != nullptr) {
            cout << cur->next->val << " ";
            cur = cur->next;
        }
        cout << endl;
    }

private:
    int _size;
    LinkedNode * _dummyHead;
};

int main(int argc, char *argv[]) {
    MyLinkedList linkedList;
    linkedList.addAtHead(1);
    linkedList.addAtTail(3);
    linkedList.addAtIndex(1, 2);
    cout << linkedList.get(1) << endl;
    linkedList.deleteAtIndex(1);
    cout << linkedList.get(1) << endl;
    linkedList.printLinkedList();
    
    return 0;
}

3. 反转链表

206. 反转链表
题意：反转一个单链表。

• 示例: 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL
• 提示
  链表中节点的数目范围是 [0, 5000]
  -5000 <= Node.val <= 5000

3.1 思路

• 如果再定义一个新的链表，实现链表元素的反转，其实这是对内存空间的浪费。其实只需要改变链表的 next 指针的指向，直接将链表反转，而不用重新定义一个新的链表，如图所示

• 之前链表的头节点是元素 1， 反转之后头结点就是元素 5 ，这里并没有添加或者删除节点，仅仅是改变 next 指针的方向。（纠正：动画应该是先移动 pre，再移动 cur）

• 首先定义一个 cur 指针，指向头结点，再定义一个 pre 指针，初始化为 null

• 然后开始反转，首先要把 cur->next 节点用 tmp 指针保存一下，因为接下来要改变 cur->next 的指向了，将 cur->next 指向 pre ，此时已经反转了第一个节点

• 接下来，就是循环走如下代码逻辑了，继续移动 pre 和 cur 指针

• 最后，cur 指针已经指向了null，循环结束，链表也反转完毕了。此时 return pre 指针就可以了，pre 指针就指向了新的头结点

3.2 代码实现

• 双指针法

// 时间复杂度: O(n)
// 空间复杂度: O(1)
#include <iostream>
using namespace std;

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    ListNode *reverseList(ListNode *head) {
        ListNode *tmp; // 保存 cur 的下一个节点
        ListNode *cur = head;
        ListNode *pre = NULL;
        // 当 cur 为空的时候循环结束，不断将 cur 指向 pre 的过程
        while (cur) {
            tmp = cur->next; // 保存 cur 的下一个节点，因为接下来要改变 cur->next
            cur->next = pre; // 翻转操作
            // 更新 pre 和 cur 指针
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
};

int main(int argc, char *argv[]) {
    ListNode *head = new ListNode(1);
    head->next = new ListNode(2);
    head->next->next = new ListNode(3);
    head->next->next->next = new ListNode(4);

    Solution solution;
    // 指向反转后链表头部的指针
    ListNode *reversedHead = solution.reverseList(head);

    // 遍历并输出一个反转后的链表中所有节点的值
    while (reversedHead) {
        cout << reversedHead->val << endl;
        reversedHead = reversedHead->next;
    }
    
    return 0;
}

• 递归法

// 时间复杂度: O(n), 要递归处理链表的每个节点
// 空间复杂度: O(n), 递归调用了 n 层栈空间
#include <iostream>
using namespace std;

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    ListNode* reverse(ListNode* pre,ListNode* cur){
        if(cur == NULL) return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        // 可以和双指针法的代码进行对比，如下递归的写法，其实就是做了这两步
        // pre = cur;
        // cur = temp;
        return reverse(cur,temp);
    }
    ListNode* reverseList(ListNode* head) {
        // 和双指针法初始化是一样的逻辑
        // ListNode* cur = head;
        // ListNode* pre = NULL;
        return reverse(NULL, head);
    }

};

int main(int argc, char *argv[]) {
    ListNode *head = new ListNode(1);
    head->next = new ListNode(2);
    head->next->next = new ListNode(3);
    head->next->next->next = new ListNode(4);

    Solution solution;
    // 指向反转后链表头部的指针
    ListNode *reversedHead = solution.reverseList(head);

    // 遍历并输出一个反转后的链表中所有节点的值
    while (reversedHead) {
        cout << reversedHead->val << endl;
        reversedHead = reversedHead->next;
    }
    
    return 0;
}

4. 两两交换链表中的节点

24. 两两交换链表中的节点
给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）

• 示例 1
  
  输入：head = [1,2,3,4]
  输出：[2,1,4,3]
• 示例 2
  输入：head = []
  输出：[]
• 示例 3
  输入：head = [1]
  输出：[1]

4.1 思路

使用虚拟头结点会方便很多，要不然每次针对头结点（没有前一个指针指向头结点），还要单独处理

• 初始时，cur 指向虚拟头结点，然后进行如下三步

• 操作之后，链表如下

4.2 代码实现

// 时间复杂度: O(n)
// 空间复杂度: O(1)
#include <iostream>
using namespace std;

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    ListNode *swapPairs(ListNode *head) {
        ListNode *dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向 head，这样方便后面做删除操作

        ListNode *cur = dummyHead;
        // 循环条件是 cur 所指节点的后面有至少两个节点，即可以进行交换
        // 如果不满足循环条件，则直接返回原链表头节点指针
        while (cur->next != nullptr && cur->next->next != nullptr) {
            // 创建两个中间指针 tmp 和 tmp1 ，分别用于暂存当前节点和下一个节点后面的节点
            ListNode *tmp = cur->next;
            ListNode *tmp1 = cur->next->next->next;

            cur->next = cur->next->next;  // 步骤一：首先将 cur 指向的节点指向下一个节点
            cur->next->next = tmp;        // 步骤二：然后将下一个节点指向 cur 节点
            cur->next->next->next = tmp1; // 步骤三：最后将 cur 节点的下一个节点指向 tmp1

            cur = cur->next->next; // cur 移动两位，准备下一轮交换
        }
        return dummyHead->next; // 返回虚拟头节点 dummyHead 指向的下一个节点，即为交换后的链表头节点
    }
};

int main() {
    ListNode *head = new ListNode(1);
    head->next = new ListNode(2);
    head->next->next = new ListNode(3);
    head->next->next->next = new ListNode(4);

    Solution solution;
    ListNode *newHead = solution.swapPairs(head);

    while (newHead != NULL) {
        cout << newHead->val << " ";
        newHead = newHead->next;
    }
    cout << endl;

    return 0;
}

5. 删除链表的倒数第 N 个节点

19. 删除链表的倒数第 N 个结点
给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点

• 示例 1
  
  输入：head = [1,2,3,4,5], n = 2
  输出：[1,2,3,5]
• 示例 2
  输入：head = [1], n = 1
  输出：[]
• 示例 3
  输入：head = [1,2], n = 1
  输出：[1]

5.1 思路

• 双指针法：如果要删除倒数第 n 个节点，让 fast 移动 n 步，然后让 fast 和 slow 同时移动，直到 fast 指向链表末尾，最后删掉 slow 所指向的节点就可以了

  • 定义 fast 指针和 slow 指针，初始值为虚拟头结点
    

  • fast 首先走 n + 1 步 ，因为只有这样同时移动的时候 slow 才能指向删除节点的上一个节点（方便做删除操作）
    

  • fast 和 slow 同时移动，直到 fast 指向末尾
    

  • 删除 slow 指向的下一个节点
    

5.2 代码实现

// 时间复杂度: O(n)
// 空间复杂度: O(1)
#include <iostream>
using namespace std;

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    ListNode *removeNthFromEnd(ListNode *head, int n) {
        ListNode *dummyHead = new ListNode(0);
        dummyHead->next = head;
        // 定义 fast 指针和 slow 指针，初始值为虚拟头结点
        ListNode *slow = dummyHead;
        ListNode *fast = dummyHead;

        // 快指针 fast 向前移动 n 个位置，直到 fast 为空或者 n 为 0
        // 在此期间，慢指针 slow 保持不动
        while (n-- && fast != NULL) {
            fast = fast->next;
        }
        // 快指针 fast 再向前移动一个位置，使得它和慢指针 slow 之间隔了 n 个节点
        // 因为需要让 slow 指向删除节点的上一个节点
        fast = fast->next; 
        // fast 和 slow 同时移动，直到 fast 指向末尾节点
        // 而慢指针 slow 指向的则是要删除的节点的前一个节点
        while (fast != NULL) {
            fast = fast->next;
            slow = slow->next;
        }
        // 将慢指针 slow 的 next 指针指向要删除节点的下一个节点
        // 从而完成了从链表中删除第 n 个节点的操作
        slow->next = slow->next->next;
        return dummyHead->next; // 获得修改后的链表头节点
    }
};

int main(int argc, char *argv[]) {
    ListNode *head = new ListNode(1);
    head->next = new ListNode(2);
    head->next->next = new ListNode(3);
    head->next->next->next = new ListNode(4);

    Solution solution;
    ListNode *newHead = solution.removeNthFromEnd(head, 2);

    while (newHead != NULL) {
        cout << newHead->val << " ";
        newHead = newHead->next;
    }
    cout << endl;
    
    return 0;
}

6. 相交链表

160. 相交链表
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null。图示两个链表在节点 c1 开始相交，题目数据保证整个链式结构中不存在环。注意，函数返回结果后，链表必须保持其原始结构

• 示例 1
  
  输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
  输出：Intersected at ‘8’
  解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
  从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
  在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
  请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。
• 示例 2
  
  输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
  输出：Intersected at ‘2’
  解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
  从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
  在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。
• 示例 3
  
  输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
  输出：null
  解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
  由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
  这两个链表不相交，因此返回 null 。

6.1 思路

求两个链表交点节点的指针（交点不是数值相等，而是指针相等）

• 为了方便举例，假设节点元素数值相等，则节点指针相等。看如下两个链表，目前 curA 指向链表 A 的头结点，curB 指向链表 B 的头结点

• 求出两个链表的长度，并求出两个链表长度的差值，然后让 curA 移动到和 curB 末尾对齐的位置

• 此时就可以比较 curA 和 curB 是否相同，如果不相同，同时向后移动 curA 和 curB，如果遇到 curA == curB，则找到交点；否则循环退出返回空指针

6.2 代码实现

// 时间复杂度：O(n + m)
// 空间复杂度：O(1)
#include <iostream>
using namespace std;

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *curA = headA;
        ListNode *curB = headB;
        // 计算两个链表的长度
        // 首先将 curA 和 curB 重置为头结点，然后遍历链表并计算链表的长度 lenA 和 lenB
        int lenA = 0, lenB = 0;
        while (curA != NULL) {
            lenA++;
            curA = curA->next;
        }
        while (curB != NULL) {
            lenB++;
            curB = curB->next;
        }

        // 将 curA 设置为较长的链表的头结点，curB 设置为较短的链表的头结点
        // 这样确保了 curA 和 curB 在移动时所经过的节点数相同
        curA = headA;
        curB = headB;
        if (lenB > lenA) {
            swap(lenA, lenB);
            swap(curA, curB);
        }

        // 计算 curA 和 curB 长度差，并移动 curA 到与 curB 末尾对齐的位置
        int gap = lenA - lenB;
        while (gap--) {
            curA = curA->next;
        }

        // curA 和 curB 同时移动，直到它们指向同一个节点或者都走到链表的末尾
            // 如果它们指向同一个节点，则返回该节点的指针
            // 否则，返回 NULL，表示两个链表没有交点
        while (curA != NULL) {
            if (curA == curB) {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        return NULL;
    }
};

int main(int argc, char *argv[]) {
    // 构建链表 A: 4 -> 1 -> 8 -> 4 -> 5
    ListNode *a1 = new ListNode(4);
    ListNode *a2 = new ListNode(1);
    ListNode *a3 = new ListNode(8);
    ListNode *a4 = new ListNode(4);
    ListNode *a5 = new ListNode(5);
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;

    // 构建链表 B: 5 -> 0 -> 1 -> 8 -> 4 -> 5
    ListNode *b1 = new ListNode(5);
    ListNode *b2 = new ListNode(0);
    ListNode *b3 = new ListNode(1);
    b1->next = b2;
    b2->next = b3;
    b3->next = a3;

    Solution solution;
    ListNode *result = solution.getIntersectionNode(a1, b1);

    if (result != NULL) {
        cout << result->val << endl;
    } else {
        cout << " NULL " << endl;
    }
    
    return 0;
}

7. 环形链表II

142. 环形链表II
给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改链表

• 示例 1
  
  输入：head = [3,2,0,-4], pos = 1
  输出：返回索引为 1 的链表节点
  解释：链表中有一个环，其尾部连接到第二个节点
• 示例 2
  
  输入：head = [1,2], pos = 0
  输出：返回索引为 0 的链表节点
  解释：链表中有一个环，其尾部连接到第一个节点
• 示例 3
  
  输入：head = [1], pos = -1
  输出：返回 null
  解释：链表中没有环

7.1 思路

• 主要考察两个知识点
  判断链表是否环
  如果有环，如何找到这个环的入口

7.1.1 判断链表是否有环

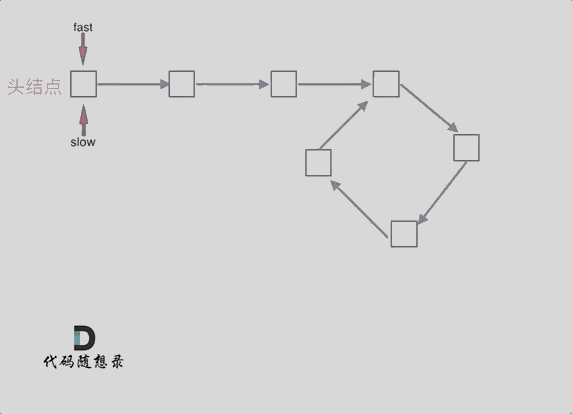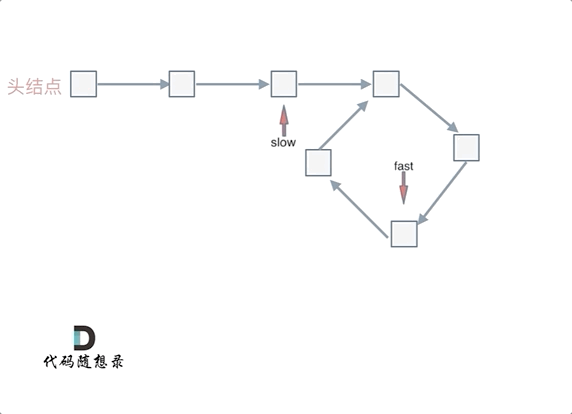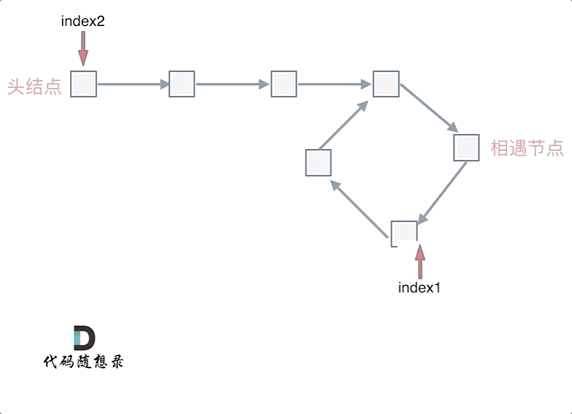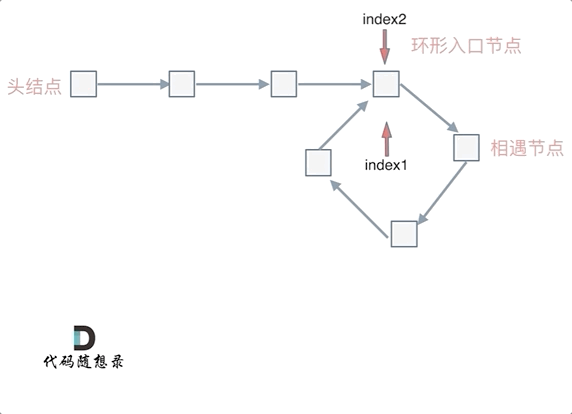
• 可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast 指针每次移动两个节点，slow 指针每次移动一个节点，如果 fast 和 slow 指针在途中相遇，说明这个链表有环

为什么 fast 走两个节点，slow 走一个节点，有环的话，为什么一定会在环内相遇呢，而不是永远错开呢？

• 首先第一点：fast 指针一定先进入环中，如果 fast 指针和 slow 指针相遇的话，一定是在环中相遇
• 那为什么 fast 指针和 slow 指针一定会相遇呢？
  可以画一个环，然后让 fast 指针在任意一个节点开始追赶 slow 指针，如下图：fast 和 slow 各自再走一步，fast 和 slow 就相遇了，这是因为 fast 是走两步，slow 是走一步，其实相对于 slow 来说，fast 是一个节点一个节点的靠近 slow 的，所以 fast 一定可以和 slow 相遇

7.1.2 如果有环，如何找到这个环的入口

• 假设从头结点到环形入口节点的节点数为 x。环形入口节点到 fast 指针与 slow 指针相遇节点节点数为 y。从相遇节点再到环形入口节点节点数为 z。那么相遇时：slow 指针走过的节点数为：x+y，fast 指针走过的节点数：x + y + n (y+z)，n 为 fast 指针在环内走了 n 圈才遇到 slow 指针，（y+z）为一圈内节点的个数

• fast 指针每步两个节点，slow 指针每步一个节点，所以：fast 指针走过的节点数 = slow 指针走过的节点数 * 2
  $$(x+y)\ast 2=x+y+n(y+z)$$
• 两边消掉一个（x+y）
  $$x+y=n(y+z)$$
• 因为要找环形的入口，那么要求的是 x，因为 x 表示头结点到环形入口节点的距离
  $$x=n(y+z)-y$$
• 再从 n(y+z) 中提出一个（y+z）来，整理公式之后为如下公式
  $$x=(n-1)(y+z)+z$$

注意这里 n 一定是大于等于 1 的，因为 fast 指针至少要多走一圈才能相遇 slow 指针

• n = 1 时，意味着 fast 指针在环形里转了一圈之后，就遇到了 slow 指针
  1. 此时公式就化解为 x = z，意味着从头结点出发一个指针，从相遇节点也出发一个指针，这两个指针每次只走一个节点，那么当这两个指针相遇的时候就是环形入口的节点
  2. 也就是在相遇节点处，定义一个指针 index1，在头结点处定一个指针 index2。让 index1 和 index2 同时移动，每次移动一个节点，那么他们相遇的地方就是环形入口的节点
• n > 1 时，就是 fast 指针在环形转 n 圈之后才遇到 slow 指针
  其实这种情况和 n = 1 效果是一样的，一样可以通过这个方法找到环形的入口节点，只不过，index1 指针在环里多转了 (n-1) 圈，然后再遇到 index2，相遇点依然是环形的入口节点

7.2 代码实现

// 时间复杂度: O(n)
    // 快慢指针相遇前，指针走的次数小于链表长度
    // 快慢指针相遇后，两个 index 指针走的次数也小于链表长度，总体为走的次数小于 2n
// 空间复杂度: O(1)
#include <iostream>
using namespace std;

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        // 定义两个指针 fast 和 slow，初始值都指向链表头结点
        ListNode *fast = head;
        ListNode *slow = head;
        while (fast != NULL && fast->next != NULL) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast) { // 说明链表中存在环
                // 定义两个指针 index1 和 index2，分别指向链表中相遇的节点和链表头结点
                ListNode *index1 = fast;
                ListNode *index2 = head;
                // 将 index1 和 index2 同时向后移动，直到它们相交，则相交点即为环的起始节点
                while (index1 != index2) {
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index2;
            }
        }
        return NULL; // 链表中不存在环，则返回空指针
    }
};

int main(int argc, char *argv[]) {
    ListNode *node1 = new ListNode(3);
    ListNode *node2 = new ListNode(2);
    ListNode *node3 = new ListNode(0);
    ListNode *node4 = new ListNode(-4);

    node1->next = node2;
    node2->next = node3;
    node3->next = node4;
    node4->next = node2; // 构造一个带环链表：-4 -> 2

    Solution solution;
    ListNode *res = solution.detectCycle(node1);

    if (res != NULL) {
        cout <<  res->val << endl;
    } else {
        cout << "NULL!" << endl;
    } 
    
    return 0;
}