题目建议： 本题关键在于理解滑动窗口，这个滑动窗口看文字讲解 还挺难理解的，建议大家先看视频讲解。  拓展题目可以先不做。

题目链接：力扣 

思路一：直接暴力计算，时间很长，不建议。
思路二：双指针法，使用两个指针将中间的数组提取出来。
双指针一般是使用一个for循环做了两个for循环的事情。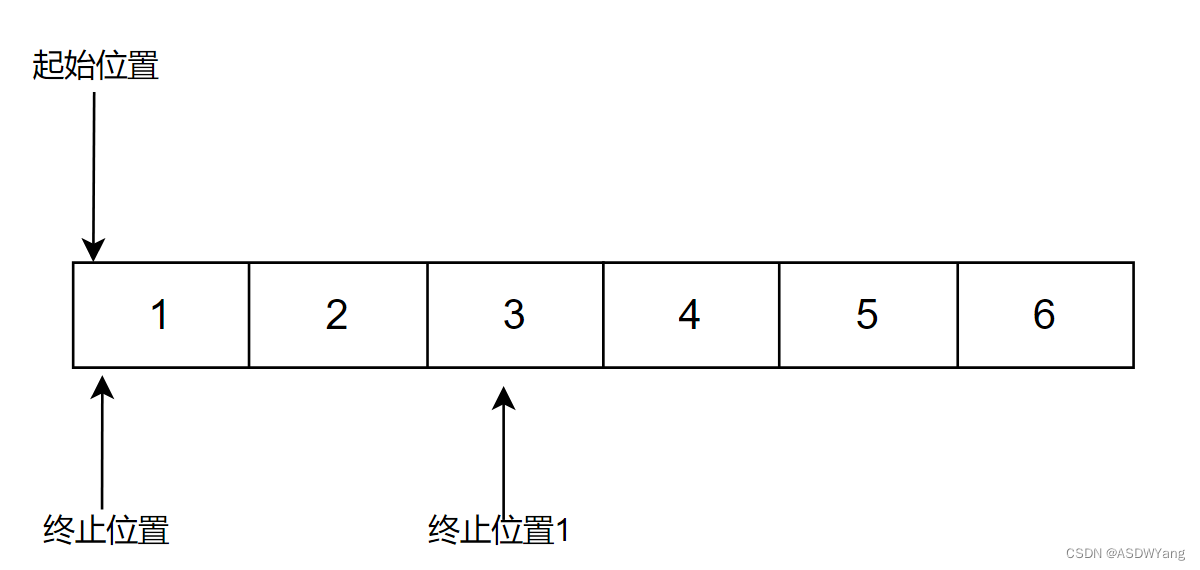

起始位置使用i表示，终止位置使用j表示。起始位置与终止位置之间的差距大于等于s，则进行改变。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        
        int result = INT32_MAX;//声明最大的长度
        int i = 0;//起始位置
        int sum = 0;//和

        int length = INT32_MAX;//长度

        for(int j = 0;j<nums.size();j++)//终止位置
        {
            sum+=nums[j];
            while(sum>=target)//注意是while
            {
                
                length = j - i + 1;
                sum = sum-nums[i];
                i++;//起始位置向前移动
                result = result < length ? result : length;
            }
            


        }
        return result<INT32_MAX?result:0;

    }
};

题目链接：力扣

关键在于四个边界的条件处理，一入循环深似海。注意循环不变量，坚持一个规则处理每一个边，按照左闭右开的规则。

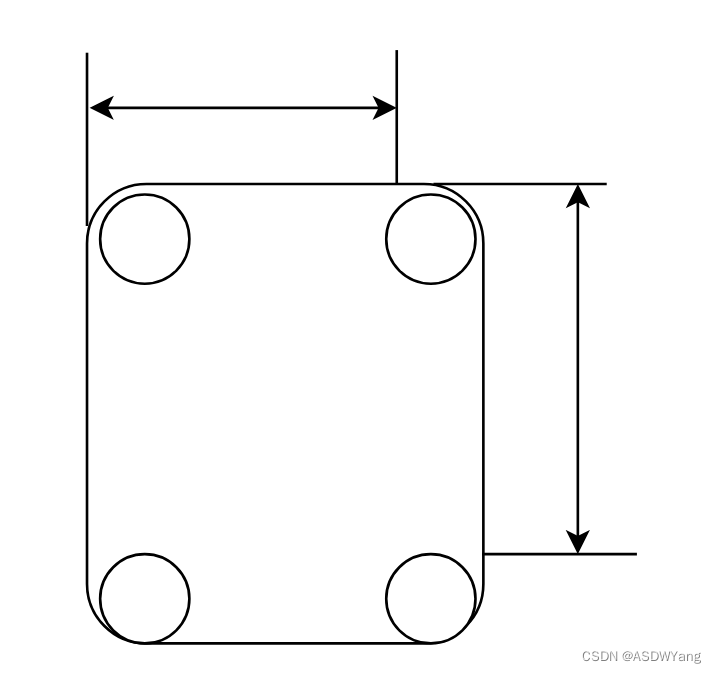
由于一圈等于两行两列，因此，转动的是n/2圈。需要判断转动的圈数是奇数还是偶数。左闭右开，终止位置是不包含的。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        //起始位置
        int startx = 0;
        int starty = 0;

        //偏移量
        int offset = 1;

        //声明一个二维数组
        vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组

        //加入的数字
        int count = 1;

        //转动圈数
        int circle = n/2;
        while(circle--)//转动的圈数
        {
            int i,j;
            for( j = starty;j<n-offset;j++)//第一行
            {
                res[startx][j]=count++;
            }
            for( i = startx;i<n-offset;i++)//右侧第一列
            {
                 res[i][j]=count++;
            }
            for(;j>starty;j--)//下侧第一列
            {
                 res[i][j]=count++;
            }
            for(;i>startx;i--)
            {
                 res[i][j]=count++;
            }
            startx++;
            starty++;
            offset++;
        }
        if(n%2 == 1)
        {
            res[n/2][n/2]=n*n;
        }
        return res;
    }
};